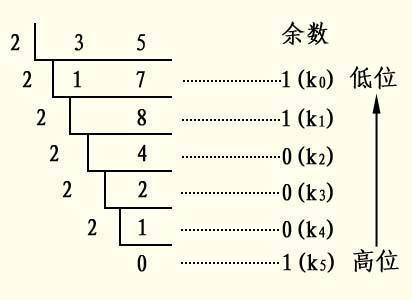
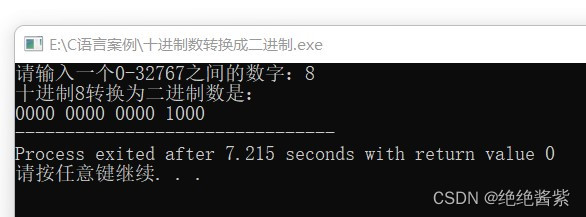
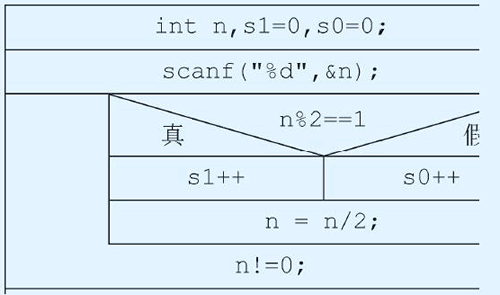
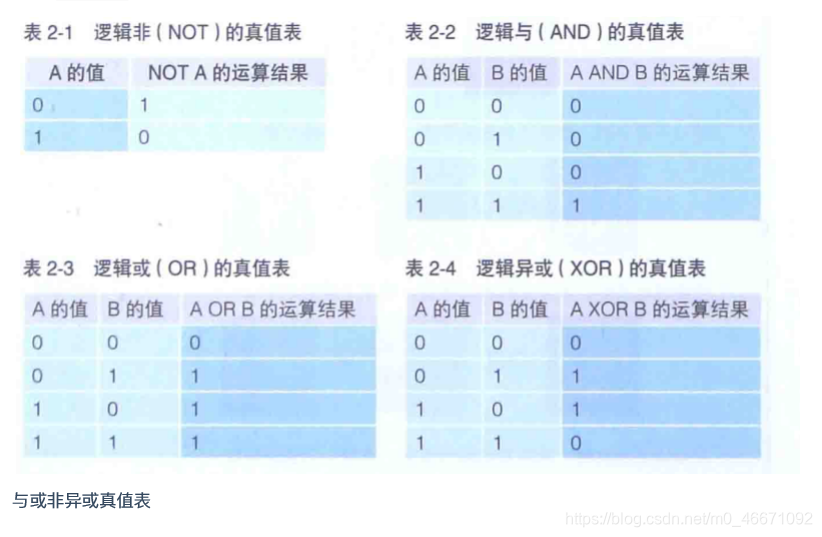
AvalonDock的基本用法
- 介绍
- AvalonDock库中的基本类
- DockingManager:停靠管理器类
- LayoutRoot : 布局根节点类
- LayoutPanel:布局面板类
- LayoutAnchorablePane:可停靠窗格类
- LayoutAnchorable:可停靠内容类
- LayoutDocumentPane:文档窗格类
- LayoutDocument:文档类
- LayoutAnchorablePaneGroup:可停靠窗格组类
- LayoutDocumentPaneGroup:文档窗格组类
- 小结
- 具体的用法
- 1. 通过Nuget添加 AvalonDock控件
- 2. 引用命名空间
- 3. 添加布局面板
- 4. 运行效果
介绍
AvalonDock 是一个开源项目,用于创建可停靠式布局,能够在WPF中方便开发出类似VS2010的软件界面。
下载地址:http://avalondock.codeplex.com/releases/view/107371
AvalonDock效果截图

AvalonDock库中的基本类
AvalonDock库中提供了一些基本的类,熟悉这些类的功能是使用AvalonDock的第一步。
DockingManager:停靠管理器类
DockingManage是AvalonDock中的核心控件之一,负责管理浮动窗体、布局存储、恢复,样式主题等。在XAML中,是AvaDock元素的根节点。
LayoutRoot : 布局根节点类
LayoutRoot 是DockingManager中的内容控件完全占满DockingManager中的空间。
LayoutRoot属性:LeftSide,RightSide,TopSide,BottomSide,分别用于展示DockingManager中左右上下四个位置的内容,但初始状态为隐藏状态。
FloatingWindows,Hidden分别为浮动窗体集合和隐藏窗体集合。当一个窗格浮动时,AvalonDock会将其从其所在组中删除,然后放置到FloatingWindows集合中。当一个窗格关闭时,会将其放置在Hidden集合中。
LayoutPanel:布局面板类
LayoutPanel是LayoutRoot中的内容控件,完全占满LayoutRoot中的空间;在LayoutPanel中,可以有多个LayoutGroup;
LayoutPanel可以设定Orientation 属性,控件布局组的浮动方向。实际的窗格都位于LayoutPanel节点下。
LayoutAnchorablePane:可停靠窗格类
可浮动窗格是可停靠控件LayoutAnchorable的容器。
一个窗格中,可以有多个可停靠控件。浮动窗格中的可停靠控件只能是LayoutAnchorable.窗格大小设定后,不能自动改变。
LayoutAnchorable:可停靠内容类
一般放置在LayoutAnchorablePane中,其内容可以是用户自定义控件类型,比如,在UserControl中设置好WPF基础控件布局,然后将整个UserControl放置在LayoutAnchorable中,这样,整个UserControl内容就可以随着可停靠控件一起浮动或者停靠。
LayoutDocumentPane:文档窗格类
与LayoutAnchorablePane类似,也是可停靠控件的容器; 文档窗格类中可以放置可停靠控件LayoutAnchorable,也可以放置文档控件LayoutDocument;
LayoutDocunemtPane会自动占满窗体的窗体布局中的剩余空间。
LayoutDocument:文档类
与LayoutAnchorable功能类似,区别在于LayoutDoucument会随着LayoutDocumentPane一起占满窗体剩余空间。
LayoutAnchorablePaneGroup:可停靠窗格组类
LayoutAnchorablePaneGroup是可停靠窗格LayoutAnchorablePane的容器。通过设置Orientation 属性,用于管理多个可停靠窗格的浮动方向。
LayoutDocumentPaneGroup:文档窗格组类
LayoutDocumentPaneGroup是文档窗格LayoutDocumentPane的容器。通过设置Orientation 属性,用于管理多个文档窗格的浮动方向。
小结
其实AvalonDock中的类有着明显的层次结构,就是容器的嵌套。DockingManager作为顶层容器,然后包含一个LayoutRoot对象,LayoutRoot中又包含一个LayoutPanel对象。LayoutPanel中便是LayoutAnchroablePane对象和LayouDocumentPane对象的集合。同时,可以对LayoutAnchroablePane对象和LayouDocumentPane对象进行分组,每个组可以单独设定组内的浮动方向。LayoutAnchorablePane又是LayoutAnchorable的容器,LayioutDocumanePane又是LayoutDocument的容器。一层一层进行嵌套,在最后的LayoutAnchorable中或者LayoutDocument中,我们放入我们真正的控件对象,这样,就可以对他们进行分类摆放布局
具体的用法
下面介绍具体的用法。
1. 通过Nuget添加 AvalonDock控件


2. 引用命名空间
xmlns:AvDock="http://schemas.xceed.com/wpf/xaml/avalondock"
3. 添加布局面板
<AvDock:DockingManager><AvDock:LayoutRoot><AvDock:LayoutPanel Orientation="Horizontal"><AvDock:LayoutAnchorablePaneGroup x:Name="LeftPanels"><AvDock:LayoutAnchorablePane DockWidth="100"></AvDock:LayoutAnchorablePane><AvDock:LayoutAnchorablePane DockWidth="200" x:Name="LeftPanel1"><AvDock:LayoutAnchorable x:Name="LeftPanel1Region" Title="LeftPanel1Region"></AvDock:LayoutAnchorable></AvDock:LayoutAnchorablePane></AvDock:LayoutAnchorablePaneGroup><AvDock:LayoutAnchorablePaneGroup x:Name="RightPanels"><AvDock:LayoutAnchorablePane DockWidth="300" x:Name="RightPanel1"><AvDock:LayoutAnchorable x:Name="RightPanel1Region" Title="RightPanel1Region"></AvDock:LayoutAnchorable></AvDock:LayoutAnchorablePane></AvDock:LayoutAnchorablePaneGroup></AvDock:LayoutPanel></AvDock:LayoutRoot></AvDock:DockingManager>
4. 运行效果