点击上方“小白学视觉”,选择加"星标"或“置顶”
重磅干货,第一时间送达k-means算法是非监督聚类最常用的一种方法,因其算法简单和很好的适用于大样本数据,广泛应用于不同领域,本文详细总结了k-means聚类算法原理 。
目录
1. k-means聚类算法原理
2. k-means聚类算法步骤
3. k-means++聚类优化算法
4. 小批量处理的k-means聚类算法
5. k值的选取
6. k-means聚类算法不适用的几个场景
7. k-means与knn区别
8. 小结
1. k-means聚类算法原理
聚类算法性能度量的文章提到若簇类相似度好簇间的相似度差,则聚类算法的性能较好。我们基于此定义k-means聚类算法的目标函数:

其中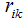 表示当样本
表示当样本 划分为簇类k时为1,否则为0。
划分为簇类k时为1,否则为0。
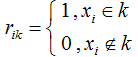
 表示簇类k的均值向量。
表示簇类k的均值向量。
目标函数(1.1)在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度,J值越小则簇内样本相似度越高。最小化目标函数是一个NP难题,k-means聚类运用EM算法思想实现模型的最优化。
1)初始化K个簇的均值向量,即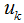 是常数,求J最小化时的
是常数,求J最小化时的 。我们不难知道当数据点划分到离该数据点最近的簇类时,目标函数J取最小。
。我们不难知道当数据点划分到离该数据点最近的簇类时,目标函数J取最小。
2)已知 ,求最小化J时相应的
,求最小化J时相应的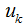 。令目标函数J对
。令目标函数J对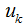 的偏导数等于0:
的偏导数等于0:

得:
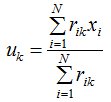
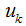 表达式的含义是簇类中心等于所属簇类样本的均值。
表达式的含义是簇类中心等于所属簇类样本的均值。
本节用EM算法思想解释了k-means聚类算法的参数更新过程,相信大家对k-means聚类算法有一个更清晰的认识。
2. k-means聚类算法步骤
k-means聚类算法步骤实质是EM算法的模型优化过程,具体步骤如下:
1)随机选择k个样本作为初始簇类的均值向量;
2)将每个样本数据集划分离它距离最近的簇;
3)根据每个样本所属的簇,更新簇类的均值向量;
4)重复(2)(3)步,当达到设置的迭代次数或簇类的均值向量不再改变时,模型构建完成,输出聚类算法结果。
3. k-means++聚类优化算法
若给定足够的迭代次数,k-means算法就能收敛,但是有可能在局部最小值点收敛。k-means收敛局部极值的原因很可能是初始化簇类中心的距离很接近,而且算法的收敛时间也加长了,为了避免这一情况,多次运行k-means聚类算法,每次运行初始化不同的簇类中心。
另一种解决k-means收敛局部极值的方法是k++聚类算法,k-means++通过让簇间中心互相远离的方案来初始化簇类中心。
具体算法步骤:
1)随机选择一个样本数据作为第一个簇类中心 ;
;
2)计算每一个样本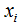 到簇类中心
到簇类中心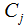 的最小距离;
的最小距离;
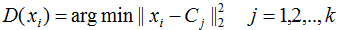
3)选择最大距离的样本点作为簇类中心;
4)重复(2)(3),直到达到簇类个数k;
5)利用这k个簇类中心作为初始化的簇类中心运行k-means算法;
4. 小批量处理的k-means聚类算法
k-means聚类算法的时间复杂度随着样本数的增加而增大,若样本量达到上万时,k-means聚类算法非常耗时,因此对该数据集进行无放回随机抽样得到合适的小批量样本数据集,sklearn.cluster包提供了相应的实现方法MiniBatchKMeans。
小批量处理的k-means聚类算法在减少了收敛时间的同时,算法结果相差不大。如下结果用inertia评价k-means和MiniBatchKmeans的算法结果。
import timeimport numpy as np
import matplotlib.pyplot as pltfrom sklearn.cluster import MiniBatchKMeans, KMeans
from sklearn.metrics.pairwise import pairwise_distances_argmin
from sklearn.datasets.samples_generator import make_blobs# Generate sample data
np.random.seed(0)
# minibatch随机抽样100例样本进行训练
batch_size = 100
centers = [[1, 1], [-1, -1], [1, -1]]
n_clusters = len(centers)
# 产生3个簇类的30000个样本数据
X, labels_true = make_blobs(n_samples=30000, centers=centers, cluster_std=0.7)# k-means++算法
k_means = KMeans(init='k-means++', n_clusters=3, n_init=10)
t0 = time.time()
k_means.fit(X)
t_batch = time.time() - t0
# MiniBatchKMeans算法
mbk = MiniBatchKMeans(init='k-means++', n_clusters=3, batch_size=batch_size,n_init=10, max_no_improvement=10, verbose=0)
t0 = time.time()
mbk.fit(X)
t_mini_batch = time.time() - t0# 打印k-means++运行时间和性能度量
print("k-means++_runtime= ",t_batch)
print("k_means++_metics= ",k_means.inertia_)
# 打印minibatch_k_means++运行时间和性能度量值
print("MiniBatch_k_means++_runtime= ",t_mini_batch)
print("k_means_metics= ",mbk.inertia_)#>
k-means++_runtime= 0.36002039909362793
k_means++_metics= 25164.97821695812
MiniBatch_k_means++_runtime= 0.15800929069519043
k_means_metics= 25178.611517320118图形结果表示:

5. 簇类个数k的选取
我们运用Calinski-Harabasz分数作为评价聚类性能的标准,分数越大,聚类性能越好,Calinski-Harabasz的含义请参考该文,
我们首先构建四个不同标准差的二维样本数据:
from sklearn import metrics
# 定义四个簇类中心
centers1 = [[0,0],[1, 1],[1.9, 2],[3, 3]]
# 定义每个簇类的标准差
std1 = [0.19,0.2,0.3,0.4]
# 算法可重复性
seed1 =45
# 产生4个簇类的30000个样本数据
X, labels_true = make_blobs(n_samples=30000, centers=centers1, cluster_std=std1,random_state=seed1)
plt.scatter(X[:,0],X[:,1],marker='o')
plt.show()数据散点图如下:
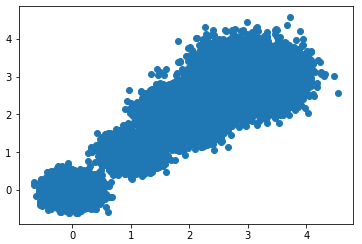
首先选择簇类个数为2,即K=2,查看聚类效果图和Calinski-Harabasz分数。
# 若我们选择k=2
k_means = KMeans(init='k-means++', n_clusters=2, n_init=10,random_state=10)
y_pred = k_means.fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()
scores2 = metrics.calinski_harabaz_score(X,y_pred)
print("the Calinski-Harabasz scores(k=2) is: ",scores2)散点图效果:
Calinski-Harabasz分数:
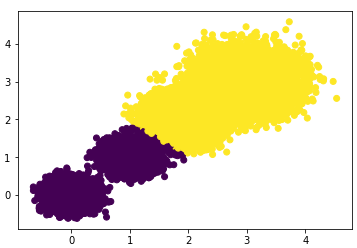
#> the Calinski-Harabasz scores(k=2) is: 85059.39875951338选择簇类个数为3,即K=3,查看聚类效果图和Calinski-Harabasz分数。
散点图效果:
Calinski-Harabasz分数:
#> the Calinski-Harabasz scores(k=3) is: 92778.08155077342选择簇类个数为4,即K=4,查看聚类效果图和Calinski-Harabasz分数。
散点图效果:
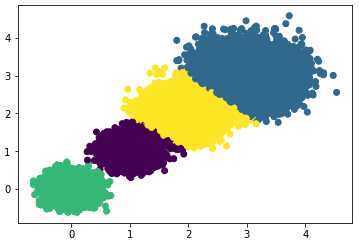
Calinski-Harabasz分数:
#> the Calinski-Harabasz scores(k=4) is: 158961.98176157777有结果可知:k=4时的Calinski-Harabasz分数最高,因此选择簇类个数为4 。
6. k-means聚类算法不适用的几个场景
k_means算法假设数据是各向同性的,即不同簇类的协方差是相等的,通俗讲就是样本数据落在各个方向的概率是相等的。
1)若样本数据是各向异性的,那么k-means算法的效果较差。
生成一组各向异性的样本数据:
import numpy as np
import matplotlib.pyplot as pltfrom sklearn.cluster import KMeans
from sklearn.datasets import make_blobsplt.figure(figsize=(6, 6))n_samples = 1500
random_state = 170
X, y = make_blobs(n_samples=n_samples, random_state=random_state)# 生成各项异性的数据
transformation = [[0.60834549, -0.63667341], [-0.40887718, 0.85253229]]
X_aniso = np.dot(X, transformation)plt.scatter(X_aniso[:, 0], X_aniso[:, 1], marker='.')
plt.title("Anisotropicly Distributed Blobs")plt.show()生成样本数据的散点图效果:
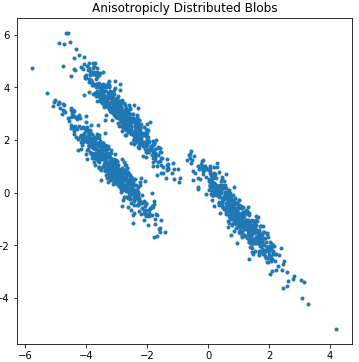
根据散点图分布,我们用簇类数k=3训练样本数据:
# k =3训练数据,输出散点效果图
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_aniso)
plt.scatter(X_aniso[:, 0], X_aniso[:, 1], marker='.',c=y_pred)
plt.title("clustering scatter distributed k=3")
plt.show()聚类效果图:
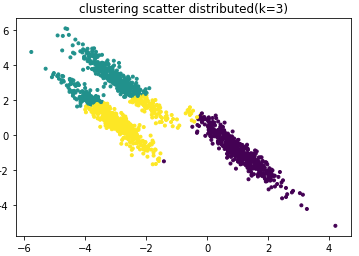
由上图可知聚类效果很差。
2)当样本数据集是非凸数据集时,k-means聚类效果较差:
首先生成非凸数据集:
# 非凸数据集
plt.figure(figsize=[6,6])
from sklearn import cluster,datasets
n_samples = 1500
noisy_circles = datasets.make_circles(n_samples=n_samples, factor=.5, noise=.05)
plt.scatter(noisy_circles[0][:,0],noisy_circles[0][:,1],marker='.')
plt.title("non-convex datasets")
plt.show()散点图效果:
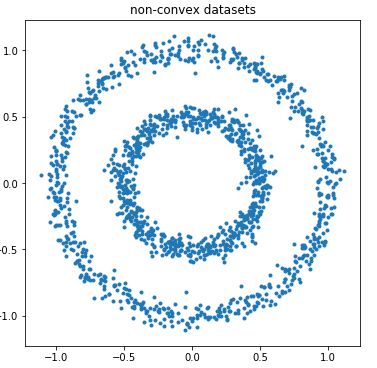
根据散点图分布,我们用簇类数k=2训练样本数据:
# k=2训练数据
y_pred = KMeans(n_clusters=2, random_state=random_state).fit_predict(noisy_circles[0])
plt.scatter(noisy_circles[0][:, 0], noisy_circles[0][:, 1], marker='.',c=y_pred)
plt.title("non-convex k-means clustering")
plt.show()散点图聚类效果:
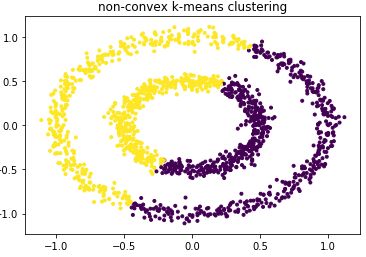
由上图可知聚类效果很差。
3)当训练数据集各个簇类的标准差不相等时,k-means聚类效果不好。
# 构建不同方差的各簇类数据,标准差分别为1.0,2.5,0.5
X_varied, y_varied = make_blobs(n_samples=n_samples,cluster_std=[1.0, 2.5, 0.5],random_state=random_state)
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_varied)plt.scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred)
plt.title("Unequal Variance")
plt.show()由下图可知聚类效果不好:

4)若各簇类的样本数相差比较大,聚类性能较差。
产生三个样本数分别为500,10,10的簇类:
n_samples = 1500
random_state = 170
# 产生三个簇类,每个簇类样本数是500
X, y = make_blobs(n_samples=n_samples, random_state=random_state)
# 三个簇类的样本数分别为500,100,10,查看聚类效果
X_filtered = np.vstack((X[y == 0][:500], X[y == 1][:100], X[y == 2][:5]))
plt.scatter(X_filtered[:, 0], X_filtered[:, 1], marker='.')
plt.title("Unequal Variance")
plt.show()散点图分布:

运用k-means对其聚类:
y_pred = KMeans(n_clusters=3,random_state=random_state).fit_predict(X_filtered)
plt.scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred,marker='.')
plt.title("Unevenly Sized Blobs")plt.show()效果图如下:
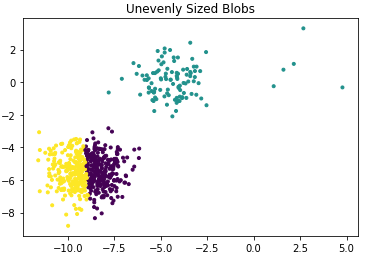
5) 若数据维度很大时,运行时间很长,可以考虑先用pca降维。
# 产生100维的15000个样本
n_samples = 15000
random_state = 170
plt.figure(figsize=[10,6])
t0=time.time()
# 产生三个簇类,每个簇类样本数是500
X, y = make_blobs(n_samples=n_samples, n_features=100,random_state=random_state)
y_pred = KMeans(n_clusters=3,random_state=random_state).fit_predict(X)
t1 =time.time()-t0
scores1 = metrics.calinski_harabaz_score(X,y)
print("no feature dimonsion reduction scores = ",scores1)
print("no feature dimonsion reduction runtime = ",t1)输出聚类效果和运行时间:
no feature dimonsion reduction scores = 164709.2183791984
no feature dimonsion reduction runtime = 0.5700197219848633数据先进行PCA降维再用k-means聚类,
# 数据先pca降维,再k-means聚类
from sklearn.decomposition import PCA
pca = PCA(n_components=0.8)
s=pca.fit_transform(X)
t0=time.time()
y_pred = KMeans(n_clusters=3,random_state=random_state).fit_predict(s)
t1 =time.time()-t0
print("feature dimonsion reduction scores = ",scores1)
print("feature dimonsion reduction runtime = ",t1)输出聚类效果和运行时间:
feature dimonsion reduction scores = 164709.2183791984
feature dimonsion reduction runtime = 0.0630037784576416由结果对比可知,聚类效果相差无几的情况下,运行时间大大降低了。
7. k-means与knn的区别
k-means是最简单的非监督分类算法,knn是最简单的监督分类算法,初学者学完监督学习章节再去学非监督章节会感觉似曾相识,原因可能都是用距离作为评价样本间的相似度。下面列举几个区别的地方:
1)knn是监督学习方法,k-means是非监督学习方法,因此knn需要样本的标记类,k-means不需要;
2)knn不需要训练,只要找到距离测试样本最近的k个样本,根据k个样本的类别给出分类结果;k-means需要训练,训练的目的是得到每个簇类的均值向量(质心),根据质心给出测试数据的分类结果;
8. 小结
k-means算法简单且在一些大样本数据表现较好而得到广泛的应用,本文也列举了k-means不适用的几个场景,其他聚类算法可能很好的解决k-means所不能解决的场景,不同的聚类算法有不同的优缺点,后续文章会持续介绍聚类算法,希望这篇k-means总结文章能帮到您。
参考
https://scikit-learn.org/stable/modules/clustering.html#clustering
https://www.cnblogs.com/pinard/p/6169370.html
好消息!
小白学视觉知识星球
开始面向外开放啦👇👇👇

下载1:OpenCV-Contrib扩展模块中文版教程在「小白学视觉」公众号后台回复:扩展模块中文教程,即可下载全网第一份OpenCV扩展模块教程中文版,涵盖扩展模块安装、SFM算法、立体视觉、目标跟踪、生物视觉、超分辨率处理等二十多章内容。下载2:Python视觉实战项目52讲
在「小白学视觉」公众号后台回复:Python视觉实战项目,即可下载包括图像分割、口罩检测、车道线检测、车辆计数、添加眼线、车牌识别、字符识别、情绪检测、文本内容提取、面部识别等31个视觉实战项目,助力快速学校计算机视觉。下载3:OpenCV实战项目20讲
在「小白学视觉」公众号后台回复:OpenCV实战项目20讲,即可下载含有20个基于OpenCV实现20个实战项目,实现OpenCV学习进阶。交流群欢迎加入公众号读者群一起和同行交流,目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群(以后会逐渐细分),请扫描下面微信号加群,备注:”昵称+学校/公司+研究方向“,例如:”张三 + 上海交大 + 视觉SLAM“。请按照格式备注,否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告,否则会请出群,谢谢理解~




![[计算机毕业设计]模糊聚类算法](https://img-blog.csdnimg.cn/632f16aceeee4be6a8443d20fb0be8d8.png)