3155 跳房子
小华正在和她的小伙伴玩跳房子游戏。这是一个加强版的跳房子,每一行的格子数量可能超过 2 个。
这个游戏需要在地面上画了n排格子,其中第i排包含a[i]个格子。(保证两端的这两排仅有一个格子)
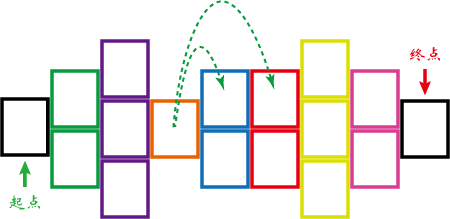
之后规定两端的这两个格子分别为起点和终点,小朋友从起点出发,每次可以跳到下一排或下两排的某个格子,直到抵达终点.
现在小华想知道从起点到终点共有多少种跳法,你能回答她的问题吗?答案对1000000007取模。
输入
第一行输入一个正整数n,其中(3 <= n <= 100000)。
第二行输入n个正整数,分别表示从起点到终点每排的格子数a[i],以空格隔开。(1 <= a
[i] <= 1000,保证起点和终点所在的排格子数为1)。输出
输出一个正整数表示跳法的数量,答案对1000000007取模。数据范围
对于100%的数据,3 <= n <= 100000,1 <= a[i] <= 1000;输入样例
6
1 1 1 1 2 1输出样例
13样例解释
第一步:跳到第二排,有1种跳法;
第二步:跳到第三排,有2种跳法;
第三步:跳到第四排,有3种跳法;
第四步:跳到第五排,有10种跳法;
第五步:跳到第六排,有13种跳法。
放代码:
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 100005;
typedef long long ll;
ll Mod = 1000000007, ans[MAXN];
int a[MAXN];
int main(){int n;cin>> n;for(int i = 0; i < n; i++)cin>> a[i];ans[0] = 1; ans[1] = a[1];for(int i = 2; i < n; i++)ans[i] = (ans[i-1] + ans[i-2]) * a[i] % Mod;cout<< ans[n-1] << endl;return 0;}