实训目标
本实训项目介绍无监督学习中，使用最广泛的 K-means 聚类算法。
先修知识
本实训项目假设，你已经掌握了初步的 Python 程序设计的基础知识。学习者若有一些 numpy 的使用经验，则可更快速地通过实训。
实训知识点
欧几里得距离
估算簇集中心
评估聚类效果
K-means算法框架

第1关：计算欧几里得距离

任务描述
本关实现一个函数来计算欧几里得距离。

相关知识
K-means 算法的核心思想是，将数据集中的样本聚类为多个簇集，簇内样本距离较近，簇间样本距离较远。由此可见，其最基本的运算是判断样本（如书籍、电影、用户、汽车等）之间的距离（或者相似度）。

通常数据集中的样本都可描述为一个 n 维向量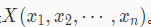
。每一个维度代表样本的一个属性。比如，对于用户 x 而言，其属性可能是收入、年龄、工作时间等，对于电影而言，其属性可能是出品年份、导演、风格等。本关卡学习欧几里得度量。

欧几里得度量（Euclidean metric）（也称欧氏距离）是一个常用的距离定义，计算 n 维空间中，两个样本点之间的几何距离。

两个在 n 维空间的点
的欧几里得距离为：

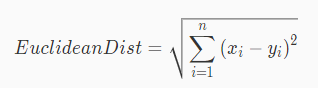
编程要求
本关卡要求你实现函数 euclid_distance，在右侧编辑器 Begin-End 区间补充代码，需要填充的代码块如下：

#-- coding: utf-8 --
import numpy as np
def euclid_distance(x1, x2):
“”“计算两个点之间点欧式距离
参数:
x1-numpy数组
x2-numpy数组
返回值：
ret-浮点型数据
“””
# 请在此添加实现代码 #
ret = 0
#********** Begin #
#* End ***********#
return ret
测试说明
平台将对你的函数输入两个 Numpy 数组，计算欧式距离，比对函数 euclid_distance 的输出结果与正确结果的差异，只有完全正确才能进入下一关。

开始你的任务吧，祝你成功！

# -*- coding: utf-8 -*-
import numpy as np
def euclid_distance(x1, x2):"""计算欧几里得距离参数:x1 - numpy数组x2 - numpy数组返回值：distance - 浮点数，欧几里得距离"""distance = 0#   请在此添加实现代码     ##********** Begin *********#import numpy as npdistance = np.sqrt(np.sum((x1-x2)**2))#********** End ***********#return distance

第2关：计算样本的最近邻聚类中心

任务描述
本关实现一个函数来计算距离每个样本最近的簇中心。

相关知识
在前一个关卡中，我们学习了欧几里得距离计算函数，对于任意两个样本，我们可以得出其距离远近。本关，我们基于这个函数，来计算距离每个样本最近的簇中心。

聚类算法中一个重要的步骤就是，来计算每个样本最近的簇中心。对于一个样本 x 和 k 个簇中心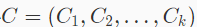
，我们可以通过如下公式计算距离 x 最近的簇 i。

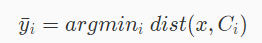
其中公式：

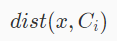
代表样本 x 与簇中心C i的欧几里得距离，argmin i代表最小值所在的序号 i。

编程要求
本关卡要求你实现函数 nearest_cluster_center，在右侧编辑器 Begin-End 区间补充代码，需要填充的代码块如下：

#-- coding: utf-8 --
#-- coding: utf-8 --
def nearest_cluster_center(x, centers):
“”“计算各个聚类中心与输入样本最近的
参数:
x - numpy数组
centers - numpy二维数组
返回值：
cindex - 整数，簇中心的索引值，比如3代表分配x到第3个聚类中
“””
cindex = -1
from distance import euclid_distance
# 请在此添加实现代码 #
#********** Begin #
#* End ***********#
return cindex
测试说明
平台将对你的函数输入一个整数向量代表样本和一个二维数组代表一组簇向量，比对函数 nearest_cluster_center 的输出结果与正确结果的差异，只有完全正确才能进入下一关。

开始你的任务吧，祝你成功！

# -*- coding: utf-8 -*-
def nearest_cluster_center(x, centers):"""计算各个聚类中心与输入样本最近的参数:x - numpy数组centers - numpy二维数组返回值：cindex - 整数，类中心的索引值，比如3代表分配x到第3个聚类中"""cindex = -1from distance import euclid_distance#   请在此添加实现代码     ##********** Begin *********##计算点到各个中心的距离n_clusters = len(centers)distance_list = []for cluster_index in range(n_clusters):distance_list.append((cluster_index, euclid_distance(x, centers[cluster_index])))#找出最小距离的类distance_list = sorted(distance_list, key=lambda s:s[1])cindex = distance_list[0][0]#********** End ***********#    return cindex

第3关：计算各聚类中心

任务描述
本关实现一个函数来计算各簇的中心。

相关知识
在前一个关卡中，我们实现了一个函数来计算距离每个样本最近的簇中心，这样每一个样本都有了所属的簇团，从而将一堆数据分成了 n 个簇，也就是 n 个类。

K-means 算法是一个迭代优化算法，每次迭代我们需要重新计算簇的中心。一般就是通过计算每个簇类所有样本的平均值来获得。可以使用 Numpy 里面的 mean 方法np.mean(x,0)来计算均值。

编程任务
本关卡要求你实现函数 estimate_centers，在右侧编辑器 Begin-End 区间补充代码，需要填充的代码块如下：

#-- coding: utf-8 --
import numpy as np
def estimate_centers(X, y_estimated, centers):
“”“重新计算各聚类中心
参数:
X - numpy二维数组，代表数据集的样本特征矩阵
y_estimated - numpy数组，估计的各个样本的聚类中心索引
n_clusters - 整数，设定的聚类个数
返回值：
centers - numpy二维数组，各个样本的聚类中心
“””
centers = np.zeros((n_clusters, X.shape[1]))
# 请在此添加实现代码 #
#********** Begin #
#* End ***********#
return centers
测试说明
输入一组向量（数据集）、一个数组（每个元素分配的类中心编号）和一组向量（各聚类中心），输出一组向量（各聚类中心）。平台比对函数 estimate_centers 的输出结果与正确结果的差异，只有完全正确才能进入下一关。

开始你的任务吧，祝你成功！

# -*- coding: utf-8 -*-
def estimate_centers(X, y_estimated, n_clusters):"""重新计算各聚类中心参数:X - numpy二维数组，代表数据集的样本特征矩阵y_estimated - numpy数组，估计的各个样本的聚类中心索引n_clusters - 整数，设定的聚类个数返回值：centers - numpy二维数组，各个样本的聚类中心"""import numpy as npcenters = np.zeros((n_clusters, X.shape[1]))#   请在此添加实现代码     ##********** Begin *********#for i in range(n_clusters):centers[i] = np.mean(X[y_estimated==i], 0)#********** End ***********#return centers    

第4关：评估聚类效果

本关任务
本关实现准确度评估函数，来评估聚类算法的效果。

相关知识
在前三个关卡中，我们学习了 K-measn 聚类算法中，三个比较关键的组成部分，包括欧几里得距离计算公式、找出每个样本的最近邻簇中心和重新计算每个簇的聚类中心。本关卡中，我们将学习评估聚类算法优劣的方法。

通常对于一个具有 K 个簇的数据集 {(x,y)}，x 是单个样本，y （1<=y<=K）是其所在的簇标识。我们的聚类算法会针对每个样本 x 输出一个他所在的簇，记为y’（1<=y’<=K）。为了评估聚类算法的效果，我们需要比较算法得出的 y’和实际数据集中的簇 y 的差异。

一种比较常见的评估聚类算法好坏的指标就是精度，定义为：

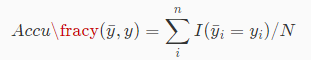
其中 N 是数据集中的样本个数，公式：

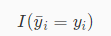
代表比较函数，若两者相等则输出 1，否则输出 0。

编程要求
本关卡要求你实现函数 acc，在右侧编辑器 Begin-End 区间补充代码，需要填充的代码块如下：

#-- coding: utf-8 --
def acc(x1, x2):
“”“计算精度
参数:
x1 - numpy数组
x2 - numpy数组
返回值：
value - 浮点数，精度
“””
value = 0
# 请在此添加实现代码 #
#********** Begin #
#* End ***********#
return value
测试说明
平台将对你的函数输入两个整数向量，比对函数 acc 的输出结果与正确结果的差异，只有完全正确才能通关。

开始你的任务吧，祝你成功！

# -*- coding: utf-8 -*-
def acc(x1, x2):"""计算精度参数:x1 - numpy数组x2 - numpy数组返回值：value - 浮点数，精度"""value = 0#   请在此添加实现代码     ##********** Begin *********#import numpy as npvalue = float(np.sum(x1==x2))/len(x1)#********** End ***********#return value

第5关：组合已实现的函数完成K-means算法

本关任务
本关综合前面四个关卡的内容来实现K-means聚类算法。

相关说明
K-means是一类非常经典的无监督机器学习算法，通常在实际应用中用于从数据集中找出不同样本的聚集模式，其基本原理就是类中样本的距离要远远小于类间样本的距离。

K-means聚类算法的流程如下：
首先从数据集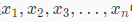

​
中随机选择k个样本作为簇中心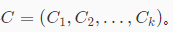

然后，进入T轮迭代，在每个迭代中执行以下两个步骤。

一、对于每个样本 x i，计算距离其最近的簇中心

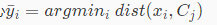
二、对于每一个簇j，重新计算其簇中心

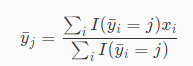
其含义实际上就是对于每一个簇j，计算分配在其中的样本向量的平均值。

编程任务
本关卡要求你完整如下代码块中星号圈出来的区域，实现K-means的核心算法步骤：

#-- coding: utf-8 --
import numpy as np
import pandas as pd
from distance import euclid_distance
from estimate import estimate_centers
from loss import acc
from near import nearest_cluster_center
#随机种子对聚类的效果会有影响，为了便于测试，固定随机数种子
np.random.seed(5)
#读入数据集
dataset = pd.read_csv(‘./data/iris.csv’)
#取得样本特征矩阵
X = dataset[[‘150’,‘4’,‘setosa’,‘versicolor’]].as_matrix()
y = np.array(dataset[‘virginica’])
#读入数据
n_clusters, n_iteration = input().split(‘,’)
n_clusters = int(n_clusters)#聚类中心个数
n_iteration = int(n_iteration)#迭代次数
#随机选择若干点作为聚类中心
point_index_lst = np.arange(len(y))
np.random.shuffle(point_index_lst)
cluster_centers = X[point_index_lst[:n_clusters]]
#开始算法流程
y_estimated = np.zeros(len(y))
#请在此添加实现代码 #
#********** Begin #
#* End ***********#
print(‘%.3f’ % acc(y_estimated, y))
测试说明
平台将比对你的实现代码与正确结果的差异，结果正确则祝贺你完成了本实训。

# -*- coding: utf-8 -*-
import numpy as np
import pandas as pd
from distance import euclid_distance
from estimate import estimate_centers
from loss import acc
from near import nearest_cluster_center
#随机种子对聚类的效果会有影响，为了便于测试，固定随机数种子
np.random.seed(5)
#读入数据集
dataset = pd.read_csv('./data/iris.csv')
#取得样本特征矩阵
X = dataset[['150','4','setosa','versicolor']].as_matrix()
y = np.array(dataset['virginica'])
#读入数据
n_clusters, n_iteration = input().split(',')
n_clusters = int(n_clusters)#聚类中心个数
n_iteration = int(n_iteration)#迭代次数
#随机选择若干点作为聚类中心
point_index_lst = np.arange(len(y))
np.random.shuffle(point_index_lst)
cluster_centers = X[point_index_lst[:n_clusters]]
#开始算法流程
y_estimated = np.zeros(len(y))
#   请在此添加实现代码     #
#********** Begin *********#
for iter in range(n_iteration):for xx_index in range(len(X)):#计算各个点最接近的聚类中心y_estimated[xx_index] = nearest_cluster_center(X[xx_index], cluster_centers)#计算各个聚类中心cluster_centers = estimate_centers(X, y_estimated, n_clusters)
#********** End ***********#
print('%.3f' % acc(y_estimated, y))

欢迎大家加我微信学习讨论