点击上方“计算机视觉工坊”，选择“星标”

干货第一时间送达

论文：https://arxiv.org/abs/2103.12040

开源代码：https://github.com/sel118/LaneAF

0

动机

车道线检测对于辅助驾驶、自动驾驶至关重要。全球范围内多种多样的车道线以及复杂的道路场景均对车道线检测算法提出了很大的挑战。

使用逐像素二分类的方法是检测车道线的主流方法，然而，二分类的输出结果并不能将不同的车道线分开；虽然有一些聚类或者实例分割的方法能够区分不同的车道线，但是它们都有最大车道线检测数量的限制。上述原因阻碍了车道线检测算法的落地。

作者提出了LaneAF算法，该方法利用Affinity Field结合二分类分割的方法进行车道线检测和实例分割，该方法性能好，且能检测数量变化的车道线。

01

算法结构

网络整体结构如下图所示：

使用DLA-34作为Backbone，网络输出二值的分割结果、Vertical Affinity Field(VAF)和Horizontal Affinity Field(HAF)。

使用HAF、VAF，结合二值分割结果，能够在后处理中对任意数量的车道线进行聚类，得到多个车道线实例。

02

Affinity Field

给定图像中的每个位置 ，HAF和VAF为每个位置分配一个向量，将HAF记作 ，将VAF记作 。

2.1 如何构建Affinity Field

使用ground truth构建HAF和VAF，将ground truth到HAF和VAF的映射函数分别记作 和 。

对于图像第 行中车道线 所包含的每个点 ，HAF由下式得到：

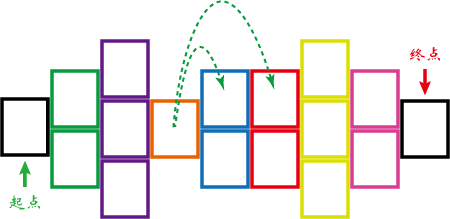
上式中的 表示第 行中属于车道线 的所有点的横坐标平均值。求解HAF的过程如下图所示：

上图中绿色框表示属于车道线 的点，蓝色框表示属于车道线 的点。箭头表示某个位置处HAF中的向量。

对于图像第 行中属于车道线 的每个点 ，VAF由下式得到：

上式中的 表示第 行中属于车道线 的所有点的横坐标平均值。求解VAF的过程如下图所示：

需要注意的是，VAF中每行的向量指向上一行中属于该车道线实例的点的平均位置。

2.2 推理时利用Affinity Field聚类

当网络训练完成后，在推理时利用HAF和VAF、结合二值分割结果进行聚类以得到车道线实例。

推理时的聚类流程如下图所示：

令 表示HAF的预测结果，对于第 行，上图中 的计算公式如下：

上式中的 和 分别表示索引为 和 的聚类中心， 表示像素点 属于哪个聚类中心。

上式表示的含义如下图所示：

上图中红色框内的点属于同一聚类。

上述算法流程图中 的计算公式为：

用来衡量车道线 与聚类中心 的距离，公式如下：

上式中的 表示网络预测的VAF， 表示属于该聚类中心的点的数量。

上式可以用下图表示：

算法流程图中的 表示与车道线 匹配的聚类中心，即：

03

损失函数

对于二值分割分支，使用带权重的二值交叉熵损失函数，权重用来解决前景和背景的类别不均衡问题，损失函数表示如下：

上式中的 表示真值， 为网络输出的结果，该值通过sigmoid函数进行归一化， 为用于平衡类别的权重。

对于分割分支，还使用了IoU损失，表示如下：

对于affinity field分支，使用L1损失函数进行回归，表示如下：

综上，整体的损失函数表示为：

04

实验结果

在具体实现时，将交叉熵损失函数中的权重 设置为9.6。LaneAF在TuSimple数据集上的测试结果如下表所示：

LaneAF在CULane数据集上的测试结果如下表所示：

在推理时，HAF和VAF的表示如下图所示：

上图中不同的颜色表示不同的车道线实例，从上图中可以看出，即使是远处相邻很近的车道线实例，也能够通过Affinity Field聚类的方法分开。

可视化的车道线检测结果如下图所示：

05

总结

这篇论文提出了LaneAF车道线检测方法，该方法在传统二值语义分割的基础上结合了Affinity Field，通过聚类实现了任意数量的车道线实例分割；通过实验证明，LaneAF具有很好的性能。

本文仅做学术分享，如有侵权，请联系删文。

下载1

在「计算机视觉工坊」公众号后台回复：深度学习，即可下载深度学习算法、3D深度学习、深度学习框架、目标检测、GAN等相关内容近30本pdf书籍。

下载2

在「计算机视觉工坊」公众号后台回复：计算机视觉，即可下载计算机视觉相关17本pdf书籍，包含计算机视觉算法、Python视觉实战、Opencv3.0学习等。

下载3

在「计算机视觉工坊」公众号后台回复：SLAM，即可下载独家SLAM相关视频课程，包含视觉SLAM、激光SLAM精品课程。

重磅！计算机视觉工坊-学习交流群已成立

扫码添加小助手微信，可申请加入3D视觉工坊-学术论文写作与投稿 微信交流群，旨在交流顶会、顶刊、SCI、EI等写作与投稿事宜。

同时也可申请加入我们的细分方向交流群，目前主要有ORB-SLAM系列源码学习、3D视觉、CV&深度学习、SLAM、三维重建、点云后处理、自动驾驶、CV入门、三维测量、VR/AR、3D人脸识别、医疗影像、缺陷检测、行人重识别、目标跟踪、视觉产品落地、视觉竞赛、车牌识别、硬件选型、深度估计、学术交流、求职交流等微信群，请扫描下面微信号加群，备注：”研究方向+学校/公司+昵称“，例如：”3D视觉 + 上海交大 + 静静“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进去相关微信群。原创投稿也请联系。

▲长按加微信群或投稿

▲长按关注公众号

3D视觉从入门到精通知识星球：针对3D视觉领域的视频课程（三维重建系列、三维点云系列、结构光系列、手眼标定、相机标定、orb-slam3等视频课程）、知识点汇总、入门进阶学习路线、最新paper分享、疑问解答五个方面进行深耕，更有各类大厂的算法工程人员进行技术指导。与此同时，星球将联合知名企业发布3D视觉相关算法开发岗位以及项目对接信息，打造成集技术与就业为一体的铁杆粉丝聚集区，近2000星球成员为创造更好的AI世界共同进步，知识星球入口：

学习3D视觉核心技术，扫描查看介绍，3天内无条件退款

 圈里有高质量教程资料、答疑解惑、助你高效解决问题

觉得有用，麻烦给个赞和在看~