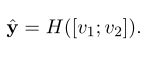线性回归中的假设检验及Python编程
- 0 引言
- 1 一元线性回归模型
- 2 对于回归方程的检验
- F检验
- T检验
- 一元线性回归的Python编程实现
- 与 `statsmodels` 包的对比
- 关于多元线性回归
0 引言
本文介绍一元线性回归的基本假设,推导方法和统计检验,然后介绍Python编程实现,最后结合Python中statsmodels包对比计算结果。
1 一元线性回归模型
对于n个自变量, ( x 1 , x 2 , x 3 , … , x n ) (x^1, x^2, x^3, \dots , x^n) (x1,x2,x3,…,xn),因变量 y i = a ∗ x i + b + ϵ i , i = 1 , 2 , … n y^i =a * x^i + b + \epsilon^i, i=1,2,\dots n yi=a∗xi+b+ϵi,i=1,2,…n,其中 ϵ i ∼ N ( 0 , σ 2 ) \epsilon^i \sim N(0, \sigma^2) ϵi∼N(0,σ2)是服从正态分布的随机变量,且彼此独立。一元线性回归的目标就是对模型参数a和b进行估计。这里需要注意 x i x^i xi不是随机变量。
利用最小二乘法对模型进行求解,首先定义代价函数:
J = ∑ i = 1 n ( y i − ( a ∗ x i + b ) ) 2 J = \sum_{i=1}^{n} (y^i - (a*x^i+b))^2 J=i=1∑n(yi−(a∗xi+b))2
将代价函数分别对a和b进行求导,并令导数为0,得到:
∂ J ∂ a = − ∑ i = 1 n 2 ∗ ( y i − ( a ∗ x i + b ) ) ∗ x i = 0 ∂ J ∂ b = − ∑ i = 1 n 2 ∗ ( y i − ( a ∗ x i + b ) ) = 0 \begin{aligned} \frac{\partial J}{\partial a} &= -\sum_{i=1}^{n}2*(y^i - (a*x^i+b))*x^i =0\\ \frac{\partial J}{\partial b} &= -\sum_{i=1}^{n}2*(y^i - (a*x^i+b)) =0 \end{aligned} ∂a∂J∂b∂J=−i=1∑n2∗(yi−(a∗xi+b))∗xi=0=−i=1∑n2∗(yi−(a∗xi+b))=0
求解得到最小而成解
a ^ = ∑ i = 1 n ( x i − x ˉ ) ∗ y i ∑ i = 1 n ( x i − x ˉ ) 2 b ^ = y ˉ − a ^ ∗ x ˉ \begin{aligned} \hat{a} &= \frac{\sum_{i=1}^{n} (x^i - \bar{x})*y^i}{\sum_{i=1}^{n} (x^i - \bar{x})^2} \\ \hat{b} &= \bar{y} - \hat{a}*\bar{x} \end{aligned} a^b^=∑i=1n(xi−xˉ)2∑i=1n(xi−xˉ)∗yi=yˉ−a^∗xˉ
其中,
x ˉ = ∑ i = 1 n x i y ˉ = ∑ i = 1 n y i \begin{aligned} \bar{x} &= {\sum_{i=1}^{n} x^i } \\ \bar{y} &= {\sum_{i=1}^{n} y^i } \end{aligned} xˉyˉ=i=1∑nxi=i=1∑nyi
2 对于回归方程的检验
在一元线性回归中(多元也一样),假设检验主要分为两类,F检验和T检验,这里分别进行介绍。
F检验
构建下面的统计量:
S S T = ∑ i = 1 n ( y i − y ˉ ) 2 S S R = ∑ i = 1 n ( y i ^ − y ˉ ) 2 S S E = ∑ i = 1 n ( y i ^ − y i ) 2 \begin{aligned} SST &= \sum_{i=1}^{n} (y^i - \bar{y})^2 \\ SSR &= \sum_{i=1}^{n} (\hat{y^i} - \bar{y})^2 \\ SSE & = \sum_{i=1}^{n} (\hat{y^i} - y^i)^2 \end{aligned} SSTSSRSSE=i=1∑n(yi−yˉ)2=i=1∑n(yi^−yˉ)2=i=1∑n(yi^−yi)2
其中 y i ^ = a ^ ∗ x i + b ^ \hat{y^i} = \hat{a}*x^i + \hat{b} yi^=a^∗xi+b^,为模型的估计值。易证 S S T = S S R + S S E SST=SSR+SSE SST=SSR+SSE(证明过程比较繁琐,但是思路比较简单,这里不再赘述)。对于空假设:
H 0 : a = 0 H 1 : a ≠ 0 H_0: a=0 \\ H_1: a \neq 0 H0:a=0H1:a=0
在空假设 H 0 H_0 H0成立的情况下, S S T / σ 2 SST/\sigma^2 SST/σ2服从自由度为 n − 1 n-1 n−1 的卡方分布,这一点在一般的概率统计中都会有介绍,不再赘述。而对于 S S E / σ 2 SSE/\sigma^2 SSE/σ2的自由度为 n − 2 n-2 n−2的证明比较复杂,可以根据经验,如果模型中需要估计p个参数,那么 S S E / σ 2 SSE/\sigma^2 SSE/σ2的自由度就为 n − p n-p n−p,这里因为要估计a和b两个参数,因而自由度为n-2。因为 S S R = S S T − S S E SSR = SST-SSE SSR=SST−SSE,从而 S S R SSR SSR服从自由度为 1 1 1的卡方分布。且SSR和SSE相互独立,从而有
F = S S R / 1 S S E / ( n − 2 ) ∼ F ( 1 , n − 2 ) F= \frac{SSR/1}{SSE/(n-2)} \sim F(1, n-2) F=SSE/(n−2)SSR/1∼F(1,n−2)
构成F统计量。在空假设成立的情况下,估计误差SSE为比较大,因而统计量F会比较小。当F取得较大值 F > F 1 − α F>F_{1-\alpha} F>F1−α是,拒绝原假设。
T检验
T检验是直接对回归系数的检验。已知
a ^ = ∑ i = 1 n ( x i − x ˉ ) ∗ y i ∑ i = 1 n ( x i − x ˉ ) 2 \hat{a} = \frac{\sum_{i=1}^{n} (x^i - \bar{x})*y^i}{\sum_{i=1}^{n} (x^i - \bar{x})^2} a^=∑i=1n(xi−xˉ)2∑i=1n(xi−xˉ)∗yi
a ^ \hat{a} a^是 y = [ y 1 , y 2 , … , y i ] T y=[y^1, y^2, \dots, y^i]^T y=[y1,y2,…,yi]T的线性组合,因而 a ^ \hat{a} a^也服从高斯分布。又因为:
E ( a ^ ) = ∑ i = 1 n ( x i − x ˉ ) ∗ E ( y i ) ∑ i = 1 n ( x i − x ˉ ) 2 = ∑ i = 1 n ( x i − x ˉ ) ∗ E ( a ∗ x i + b + ϵ i ) ∑ i = 1 n ( x i − x ˉ ) 2 = ∑ i = 1 n ( x i − x ˉ ) ∗ ( a ∗ x i + b ) ∑ i = 1 n ( x i − x ˉ ) 2 = ∑ i = 1 n a ( x i − x ˉ ) ∗ ( x i − x ˉ ) ∑ i = 1 n ( x i − x ˉ ) 2 = a \begin{aligned} E(\hat{a}) &= \frac{\sum_{i=1}^{n} (x^i - \bar{x})*E(y^i)}{\sum_{i=1}^{n} (x^i - \bar{x})^2} \\ &=\frac{\sum_{i=1}^{n} (x^i - \bar{x})*E(a*x^i+b+\epsilon^i)}{\sum_{i=1}^{n} (x^i - \bar{x})^2} \\ &=\frac{\sum_{i=1}^{n} (x^i - \bar{x})*(a*x^i+b)}{\sum_{i=1}^{n} (x^i - \bar{x})^2} \\ &=\frac{\sum_{i=1}^{n} a(x^i - \bar{x})*(x^i-\bar{x})} {\sum_{i=1}^{n} (x^i - \bar{x})^2} \\ &=a \\ \end{aligned} E(a^)=∑i=1n(xi−xˉ)2∑i=1n(xi−xˉ)∗E(yi)=∑i=1n(xi−xˉ)2∑i=1n(xi−xˉ)∗E(a∗xi+b+ϵi)=∑i=1n(xi−xˉ)2∑i=1n(xi−xˉ)∗(a∗xi+b)=∑i=1n(xi−xˉ)2∑i=1na(xi−xˉ)∗(xi−xˉ)=a
为了计算方差,我们将上述表达式定义为向量形式,首先定义向量 x μ = [ x 1 − x ˉ , x 2 − b a r x , … , x n − x ˉ ] x_{\mu} = [x^1-\bar{x}, x^2-bar{x}, \dots, x^n - \bar{x}] xμ=[x1−xˉ,x2−barx,…,xn−xˉ],则:
a ^ = x μ T y / x μ T x μ \hat{a} = x_\mu ^Ty/x_\mu^Tx_\mu a^=xμTy/xμTxμ
则估计参数的方差为:
V a r ( a ^ ) = C o v ( x μ T y / x μ T x μ , x μ T y / x μ T x μ ) = C o v ( x μ T y , x μ T y ) / ( x μ T x μ ) 2 = x μ T C o v ( y , y ) x μ / ( x μ T x μ ) 2 = x μ T σ 2 I n x μ / ( x μ T x μ ) 2 = σ 2 / ( x μ T x μ ) \begin{aligned} Var(\hat{a}) &= Cov(x_\mu ^Ty/x_\mu^Tx_\mu, x_\mu ^Ty/x_\mu^Tx_\mu) \\ &= Cov(x_\mu ^Ty, x_\mu ^Ty)/(x_\mu^Tx_\mu)^2\\ &= x_\mu^TCov(y, y)x_\mu / (x_\mu^Tx_\mu)^2\\ &= x_\mu^T\sigma^2I_nx_\mu / (x_\mu^Tx_\mu)^2\\ &=\sigma^2/(x_\mu^Tx_\mu) \\ \end{aligned} Var(a^)=Cov(xμTy/xμTxμ,xμTy/xμTxμ)=Cov(xμTy,xμTy)/(xμTxμ)2=xμTCov(y,y)xμ/(xμTxμ)2=xμTσ2Inxμ/(xμTxμ)2=σ2/(xμTxμ)
因而, a ^ ∼ N ( a , σ 2 / ( x μ T x μ ) ) \hat{a} \sim N(a, \sigma^2/(x_\mu^Tx_\mu) ) a^∼N(a,σ2/(xμTxμ)) 。又根 S S E / σ 2 SSE/\sigma^2 SSE/σ2服从自由度n-2的卡方分布,且这两个变量相互独立(这里没给出证明),可以得到统计量T:
T = a ^ − a σ / x μ T x μ / ( S S E / σ 2 / ( n − 2 ) ) ∼ t ( n − 2 ) \begin{aligned} T &= \frac{\hat{a}-a}{\sigma/\sqrt{x_\mu^Tx_\mu}} / \sqrt{ (SSE/\sigma^2/(n-2))} \\ &\sim t(n-2) \end{aligned} T=σ/xμTxμa^−a/(SSE/σ2/(n−2))∼t(n−2)
H 0 : a = 0 H 1 : a ≠ 0 H_0: a=0 \\ H_1: a \neq 0 H0:a=0H1:a=0
在空假设 H 0 H_0 H0成立时,T应该接近于0。在 ∣ a ^ ∣ > t 1 − α / 2 |\hat{a}|>t_{1-\alpha/2} ∣a^∣>t1−α/2时拒绝原假设。
一元线性回归的Python编程实现
import numpy as np
import matplotlib.pyplot as plt
from scipy import statsdef linear_ols(x, y):'''实现一元线性回归返回参数: a, b, F检验统计量及p值, T检验统计量及p值'''mu = np.mean(x)xmu = x - mua = xmu.dot(y)/xmu.dot(xmu)b = np.mean(y) - a*np.mean(x)SST = np.sum((y-np.mean(y))**2)y_pred = a*x + bSSE = np.sum((y-y_pred)**2)SSR = SST - SSEN = len(x)F = SSR/1 / (SSE/(N-2)) #F统计量pF = 1-stats.f.cdf(F, dfn = 1, dfd = N-2)T =np.sqrt(xmu.dot(xmu)) * a/np.sqrt(SSE/(N-2)) #T统计量if(a>0):pT = 2*(1-stats.t.cdf(T, df = N-2))else:pT = 2*stats.t.cdf(T, df=N-2)return a, b, F, pF, T, pT
生成仿真数据,输出结果。
N = 300
x = np.linspace(-2, 2, N)
y = 3*x + 2*np.random.randn(N)plt.plot(x, y, 'o')
a, b, F, pF, T, pT = linear_ols(x, y)
y_pred = a*x + b
plt.plot(x, y_pred)
plt.xlabel('x')
plt.ylabel('y')print('a=%.3f, b=%.3f' %(a, b))
print('F statistics = %.2f, p=%.3f'%( F, pF))
print('T statistics =%.2f, p =%.3f'%( T, pT))
得到的结果如下:

a=3.003, b=-0.100
F statistics = 983.34, p=0.000
T statistics =31.36, p =0.000
由于生成随机数的原因,不同机器运行结果可能略有差异。
与 statsmodels 包的对比
statsmodels提供了线性回归的一般解法,我们将其输出的结果与自己编写的函数进行对比。
from statsmodels import api as sm
X = sm.add_constant(x)#添加常数项
model = sm.OLS(y,X)
result = model.fit()
print(result.summary())
程序输出结果为:
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.767
Model: OLS Adj. R-squared: 0.767
Method: Least Squares F-statistic: 983.3
Date: Sun, 18 Apr 2021 Prob (F-statistic): 2.18e-96
Time: 20:39:24 Log-Likelihood: -620.69
No. Observations: 300 AIC: 1245.
Df Residuals: 298 BIC: 1253.
Df Model: 1
Covariance Type: nonrobust
==============================================================================coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -0.0999 0.111 -0.901 0.369 -0.318 0.118
x1 3.0035 0.096 31.358 0.000 2.815 3.192
==============================================================================
Omnibus: 3.843 Durbin-Watson: 1.807
Prob(Omnibus): 0.146 Jarque-Bera (JB): 3.162
Skew: -0.147 Prob(JB): 0.206
Kurtosis: 2.592 Cond. No. 1.16
==============================================================================Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
从上述结果中可以看出,const也就是我们估计结果中的b值,x1也就是我们估计结果中的a值,两者一致。F-statistics和t-statistics983.3和31.358,也和我们代码的运行结果一致。
关于statsmodels结果的解读,可以参考statsmodels中的summary解读(使用OLS)
关于多元线性回归
推导方法类似,原理类似,个人认为能够通过一元线性回归加深对问题的理解就足够了,多元线性回归在使用时直接使用工具包就行,参数的解读也是相似的。




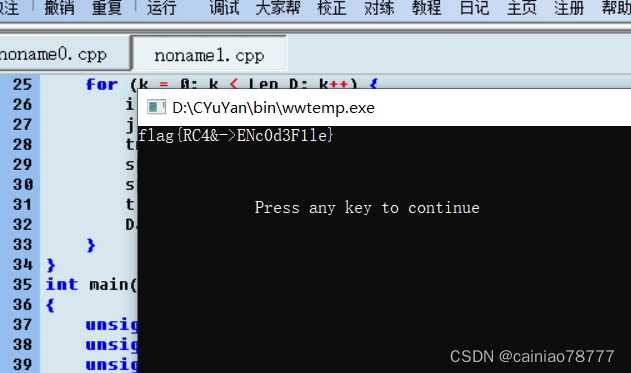
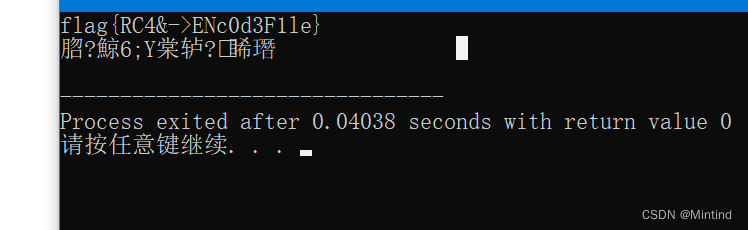
![[SWPUCTF 2021 新生赛]re2](https://img-blog.csdnimg.cn/f8f1ebefff4645c69ca58cd8d65f8741.png)