1、假设检验的步骤:
第1步:确定零假设和备选假设 零假设( H 0 H_{0} H0): 备选假设( H 1 H_{1} H1):
第2步:证据是什么?(计算p值) 在零假设成立的前提下,从总体中随机抽样得到一个样本,并计算这个样本发生的可能性有多大(P值)。
第3步:判断标准是什么?(显著性水平) 假设检验常用的判断标准是5%,在假设检验里叫做“显著水平”,用符号α,
第4步: 做出结论 如果,P值 < α 说明小概率事件发生了,则拒绝 H 0 H_{0} H0。否则接受 H 1 H_{1} H1。
例题:

分析:
第1步:确定零假设和备选假设
零假设 H 0 H_{0} H0:药物无效,即 μ = 1.2 s \mu=1.2s μ=1.2s
备选假设 H 1 H_{1} H1:药物有效,即 μ ≠ 1.2 s \mu \neq 1.2s μ=1.2s
第2步:计算p值
在假设 H 0 H_{0} H0正确的前提下,计算出样本均值 x ‾ = 1.05 \overline{x}=1.05 x=1.05、标准差 S=0.5 这一结果的概率P。
抽样分布如图:

计算出抽样分布的均值 μ x = μ = 1.2 s \mu_{\mathrm{x}}=\mu=1.2 \mathrm{s} μx=μ=1.2s,
标准差 σ x ‾ = σ 100 ≈ S 100 = 0.5 10 = 0.05 \sigma_{\overline{x}}=\frac{\sigma}{\sqrt{100}} \approx \frac{S}{\sqrt{100}}=\frac{0.5}{10}=0.05 σx=100σ≈100S=100.5=0.05
计算1.05秒离抽样分布均值有多少个标准差远,也就是 z z z 值:
z = 1.2 − 1.05 0.05 = 3 z=\frac{1.2-1.05}{0.05}=3 z=0.051.2−1.05=3
根据经验法则,3个标准差内的概率是99.7%,求出P值为1-99.7 %=0.3 %,P=0.3%。
第3步:显著性水平
显著性水平取5%。
第4步: 做出结论
如果 H 0 H_{0} H0成立,只有不到0.3%的几率得到抽样结果,P值小于 α \alpha α, 因此结果更倾向于拒绝 H 0 H_{0} H0假设,支持 H 1 H_{1} H1假设,即药物有效果。
2、单侧检验和双侧检验
在这个例题中,我们只是检验药物是否存在效果,不管是正效果还是反效果都认为是有效,这称为双侧检验。
将备选假设 H 1 H_{1} H1 改为用药降低反应时间,就变成了单侧检验。
3、z统计量和t统计量
z值代表离均值有多少个标准差远,公式可以写成:
z = x ‾ − μ x ‾ σ n z=\frac{\overline{x}-\mu_{\overline{x}}}{\frac{\sigma}{\sqrt{n}}} z=nσx−μx
但一般情况下总体标准差 σ \sigma σ 通常是未知的,当样本容量n>30时,可以用样本标准差S作为估计值,这时是符合正态分布的:
z = x ‾ − μ x ‾ S n z=\frac{\overline{x}-\mu_{\overline{x}}}{\frac{S}{\sqrt{n}}} z=nSx−μx
但如果样本容量n<30时,就不服从正态分布了,服从t分布:
t = x ‾ − μ x ‾ S n t=\frac{\overline{x}-\mu \overline{x}}{\frac{S}{\sqrt{n}}} t=nSx−μx
对应的查t值表就可以了。
4、第一类错误
第一类错误:原假设是正确的,却拒绝了原假设。(错杀好人)
第二类错误:原假设是错误的,却没有拒绝原假设。(放走坏人)
5、大样本伯努利占比假设检验
我们要检验一个假设,即超过30%美国家庭拥有互联网接入,显著性水平5%。我们采集了150个家庭作为样本,结果57家拥有接入。
分析:
第1步:确定零假设和备选假设
零假设 H 0 H_{0} H0:美国家庭网络接入<=30%
备选假设 H 1 H_{1} H1:美国家庭网络接入>30%
第2步:计算p值
我们要根据零假设得到一个总体中的占比值,在这个假设下,看150户中有57户接入网络的概率是多少?如果该概率小于5%,我们就拒绝零假设,承认备择假设。
样本均值:57/150=0.38
样本标准差:S=0.38*0.62
假设 P H 0 = 0.3 P_{H_{0}}=0.3 PH0=0.3,
零假设下,总体均值为0.3,总体标准差: σ H 0 = 0.3 × 0.7 = 0.21 \sigma_{H_{0}}=\sqrt{0.3 \times 0.7}=\sqrt{0.21} σH0=0.3×0.7=0.21
样本抽样分布:多次二项分布抽样 np>5时(p为小于1的数,np大于5 表示n的值比较大,表示这是一个大样本),该样本抽样分布满足正态分布。零假设下,np= 150*0.3 >5 ,我们认为零假设下的抽样分布满足正太分布。
所以抽样分布均值 μ \mu μ=0.3,
抽样分布标准差 σ p = σ H o 150 = 0.037 \sigma_{p}=\frac{\sigma_{H o}}{\sqrt{150}}=0.037 σp=150σHo=0.037
求样本均值与 抽样分布均值之间的标准差数,即z值:
z = 0.38 − 0.3 0.037 = 2.14 z=\frac{0.38-0.3}{0.037}=2.14 z=0.0370.38−0.3=2.14
查询Z分布表 5%的概率为1.65个标准差。而2.41 > 1.65 即 零假设下,样本均值距总体均值的距离大于5%的概率下的标准差距离,也就是样本均值落入小于5%概率下的均值分布,拒绝零假设。
6、随机变量之差的方差
结论一:随机变量之差的均值等于均值之差: μ X − Y = μ X − μ Y \mu_{X-Y}=\mu_{X}-\mu_{Y} μX−Y=μX−μY
结论二:两独立随机变量之差的方差等于两个随机变量分别的方差之和: σ X − Y 2 = σ X 2 + b Y 2 \sigma_{X-Y}^{2}=\sigma_{X}^{2}+b_{Y}^{2} σX−Y2=σX2+bY2
7、总体占比的比较
选举中,我想知道男人和女人都给某些候选人的占比是否有显著不同?
男性中 投给某候选人的占比为p1,不投给这个候选人的占比为1-p1. 投给此候选人为1,不投给此候选人为0.
女性中 投给这个候选人的占比为p2,不投给这个候选人的占比为1-p2. 投给此候选人为1,不投给此候选人为0.
这两个都是伯努利分布。
男:均值=p1,方差=p1*(1-p1)
女:均值=p2,方差=p2*(1-p2)
所求:p1 和 p2 是否有显著差异?也就是 p1 - p2的分布。
我们希望求出一个95%的置信区间,为此我们调查了1000个男性 和 1000个女性投票者。
样本男:642投了此候选人,记为1 358未投此候选人,记为0. p1 = 0.642 方差=0.6420.358
样本女:591投了此候选人,记为1 409未投此候选人,记为0. p2 = 0.591 方差=0.5910.409
由于样本容量大,所以随机抽样分布接近正态分布:
随机抽样均值分布男 总体均值=样本均值=0.642 总体方差=方差=0.6420.358/1000(大容量样本下 我们用样本方差估计总体方差)
随机抽样均值分布女 总体均值=样本均值=0.591 总体方差=方差=0.5910.409/1000(大容量样本下 我们用样本方差估计总体方差)
随机抽样均值差分布 分布均值=0.642-0.591=0.051 方差=0.6420.358/1000 + 0.5910.409/1000=0.022X0.022
差值分布95%的置信区间 查表可知 z=1.96 ,d=1.96X0.022=0.043
所以 有95%机率均总体占比之差落在样本占比之差左右0.043范围内 即:p1-p2的95%置信区间是[0.008,0.094]
假设检验:
零假设:投票男女占比无差别 即总体差值 p1-p2 = 0
备择假设:投票男女占比有差别 即总体差值 p1-p2 != 0
使用显著性水平5%进行检验
零假设下:总体差值分布的均值为0,样本差值=0.051,求出0.051距离0有几个标准差?
查Z表可知:正态分布下,2.5%的z值=1.96。如果0.051距离0的标准差数>1.96,说明样本概率小于5%,这样就可以拒绝零假设。
零假设下:p1=p2,方差有更好的估计值,即 方差=2p(1-p)/1000 p=(642+591)/2000 则标准差=0.0217
0.051/0.0217=2.35
2.35>1.96,所以我们拒绝零假设。

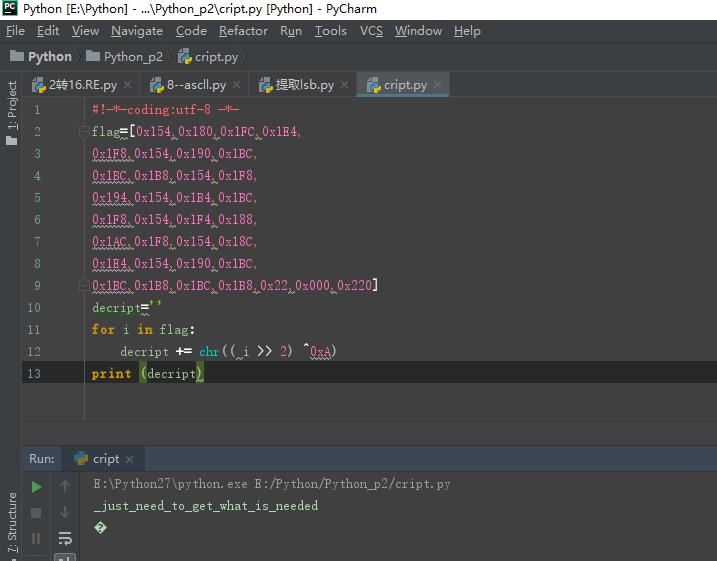
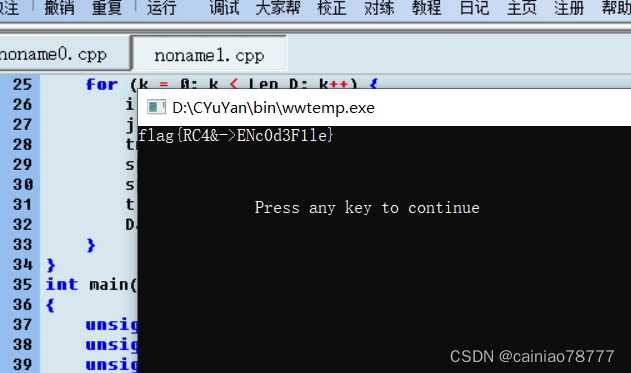
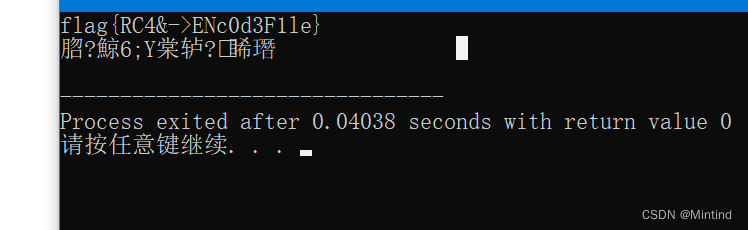
![[SWPUCTF 2021 新生赛]re2](https://img-blog.csdnimg.cn/f8f1ebefff4645c69ca58cd8d65f8741.png)