背景
前文已经介绍了【NLP】文本匹配——Enhanced LSTM for Natural Language Inference,其实2017年发表的,文中使用了两个LSTM进行特征提取,总的来说参数多,速度慢,还不能并行处理。今天我们再来看看阿里巴巴和南京大学发表的在2019年发表的一篇文本匹配论文:Simple and Effective Text Matching with Richer Alignment Features,没有使用LSTM进行特征提取,支持了并行化处理以及参数也少了很多。具体怎么做的,我们看看该论文的介绍。主要看模型的结构设计,模型相关实验可以看看原文。论文中将该算法简称为RE2.
RE2
首先说一下为什么叫做RE2吧。主要是该模型的结构包含三个重要的部分:Residual vectors、Embedding vectors、Encoded vectors。
该模型的结构如下:
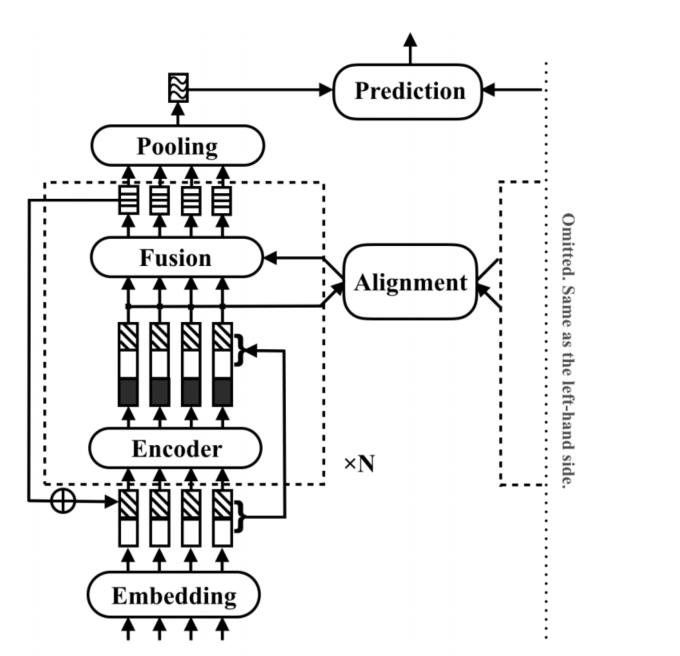
由于我们的输入包含两个句子,即sentence1和sentence2。对于输入的两个句子的处理方式相同,故省略了另一半。论文中的核心内容在section2,模型的第一层是常规的Embedding层,第二层是中间处理层,里面有N个相同的block,每个block不共享,参数独立,第三层就是输出层。
下面我们来详细看看这几层是如何做的。
Augmented Residual Connections(增强的残差连接)
为了为对齐过程提供更丰富的特性,RE2采用了增强版的残差连接来连接连续的块。对于一个长度为 l l l的序列,对于第n个块的输入与输出做以下定义,输入: x ( n ) = ( x 1 ( n ) , x 2 ( n ) , ⋯ , x l ( n ) ) x^{(n)}=(x_1^{(n)},x_2^{(n)},\cdots,x_l^{(n)}) x(n)=(x1(n),x2(n),⋯,xl(n)),输出 o ( n ) = ( o 1 ( n ) , o 2 ( n ) , ⋯ , o l ( n ) ) o^{(n)}=(o_1^{(n)},o_2^{(n)},\cdots,o_l^{(n)}) o(n)=(o1(n),o2(n),⋯,ol(n))。 o ( 0 ) o^{(0)} o(0)设置为0向量。 x ( 1 ) x^{(1)} x(1)是Embedding层的输出结果。接下来的第 n ( n ≥ 2 ) n(n\geq 2) n(n≥2)块的表示如下:
x i ( n ) = [ x i ( 1 ) ; o i ( n − 1 ) + o i ( n − 2 ) ] x_{i}^{(n)}=\left[x_{i}^{(1)} ; o_{i}^{(n-1)}+o_{i}^{(n-2)}\right] xi(n)=[xi(1);oi(n−1)+oi(n−2)]
其中 [ ; ] [;] [;]表示拼接。
对于增强的残差连接,对齐和融合层的输入有三个部分,即沿途保持不变的原始点向特征(嵌入向量),由以前的块(残差向量)处理和细化的先前对齐向量,以及来自编码器层的上下文特征(编码向量)。这三个部分在文本匹配过程中都起着互补的作用。
Alignment Layer 对齐层
对齐层将两个序列中的特征作为输入,并计算对齐的表示作为输出。从长度为 l a l_a la的第一个序列输入的输入表示为 a = ( a 1 , a 2 , ⋯ , a l a ) a=(a_1,a_2,\cdots,a_{l_a}) a=(a1,a2,⋯,ala),长度为 l b l_b lb的第二个序列表示为 b = ( b 1 , b 2 , ⋯ , b l b ) b=(b_1,b_2,\cdots,b_{l_b}) b=(b1,b2,⋯,blb)。 a i a_i ai和 b j b_j bj的相似度得分如下:
e i j = F ( a i ) T F ( b j ) e_{i j}=F\left(a_{i}\right)^{T} F\left(b_{j}\right) eij=F(ai)TF(bj)
F是一个指定的函数或一个单层前馈网络。该选择被视为一个超参数。对齐结果 a ′ a^{\prime} a′、 b ′ b^{\prime} b′计算如下:
a i ′ = ∑ j = 1 l b exp ( e i j ) ∑ k = 1 l b exp ( e i k ) b j b j ′ = ∑ i = 1 l a exp ( e i j ) ∑ k = 1 l a exp ( e k j ) a i \begin{aligned} a_{i}^{\prime} &=\sum_{j=1}^{l_{b}} \frac{\exp \left(e_{i j}\right)}{\sum_{k=1}^{l_{b}} \exp \left(e_{i k}\right)} b_{j} \\ b_{j}^{\prime} &=\sum_{i=1}^{l_{a}} \frac{\exp \left(e_{i j}\right)}{\sum_{k=1}^{l_{a}} \exp \left(e_{k j}\right)} a_{i} \end{aligned} ai′bj′=j=1∑lb∑k=1lbexp(eik)exp(eij)bj=i=1∑la∑k=1laexp(ekj)exp(eij)ai
求和通过当前位置和另一个序列中相应位置之间的相似性得分进行加权,还是一种attention。
Fusion Layer 融合层
融合层在三个角度中比较局部和对齐表示,然后将它们融合在一起。第一个序列 a ‾ \overline a a的融合层的输出计算如下:
a ˉ i 1 = G 1 ( [ a i ; a i ′ ] ) , a ˉ i 2 = G 2 ( [ a i ; a i − a i ′ ] ) , a ˉ i 3 = G 3 ( [ a i ; a i ∘ a i ′ ] ) , a ˉ i = G ( [ a ˉ i 1 ; a ˉ i 2 ; a ˉ i 3 ] ) , \begin{aligned} &\bar{a}_{i}^{1}=G_{1}\left(\left[a_{i} ; a_{i}^{\prime}\right]\right), \\ &\bar{a}_{i}^{2}=G_{2}\left(\left[a_{i} ; a_{i}-a_{i}^{\prime}\right]\right), \\ &\bar{a}_{i}^{3}=G_{3}\left(\left[a_{i} ; a_{i} \circ a_{i}^{\prime}\right]\right), \\ &\bar{a}_{i}=G\left(\left[\bar{a}_{i}^{1} ; \bar{a}_{i}^{2} ; \bar{a}_{i}^{3}\right]\right), \end{aligned} aˉi1=G1([ai;ai′]),aˉi2=G2([ai;ai−ai′]),aˉi3=G3([ai;ai∘ai′]),aˉi=G([aˉi1;aˉi2;aˉi3]),
其中G1、G2、G3、G为参数独立的单层前馈网络, ∘ \circ ∘为元素级乘法。减法算符突出了两个向量之间的差异,而乘法突出了相似性。 b ‾ \overline b b的公式类似,在这里省略了。
Prediction Layer 预测层
预测层从池化层中获取两个序列 v 1 v_1 v1和 v 2 v_2 v2的向量表示作为输入,并预测接下来的最终目标,如下:
y ^ = H ( [ v 1 ; v 2 ; v 1 − v 2 ; v 1 ∘ v 2 ] ) \hat{\mathbf{y}}=H\left(\left[v_{1} ; v_{2} ; v_{1}-v_{2} ; v_{1} \circ v_{2}\right]\right) y^=H([v1;v2;v1−v2;v1∘v2])
H是一个多层前馈神经网络。
总结
从公式来看,了解ESIM的会发现,该模型与ESIM还是比较相似,最大的不同点在于使用残差网络进行信息增强。除此之外,由于没有使用LSTM进行特征提取,其速度也会比ESIM快。