凸多边形最优三角

article/2025/9/18 12:04:26

前言：大三下算法课，自己看的凸多边形最优三角，最后上台讲解，和子涵苗子等一起的一段时间

1.相关概念

• 凸多边形：一个简单多边形及其内部构成一个闭凸集时，则称该简单多边形为一个凸多边形。

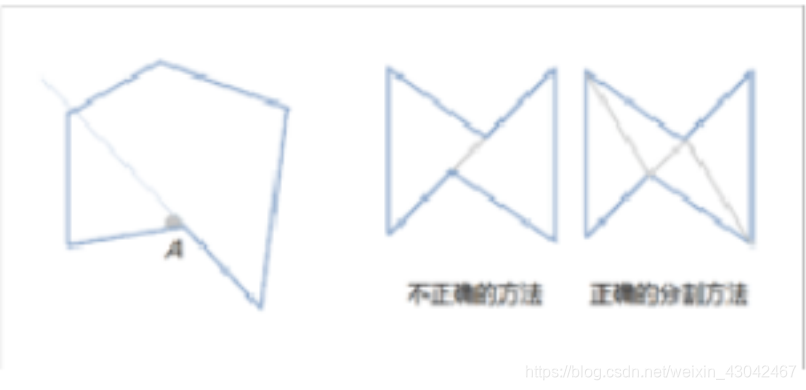
• 边：多边形相邻两点的连线

• 弦：多边形不相邻两点的连线

2.问题定义——凸多边形最优三角

• 给定凸多边形 P ，以及定义在由多边形的边和弦组成的三角形上的权函数 w 。要求确定该凸多边形的三角剖分，使得该三角剖分中所有三角形上权之和为最小。

（这个定义删减了些数学描述，只描述了问题）

相关性质：

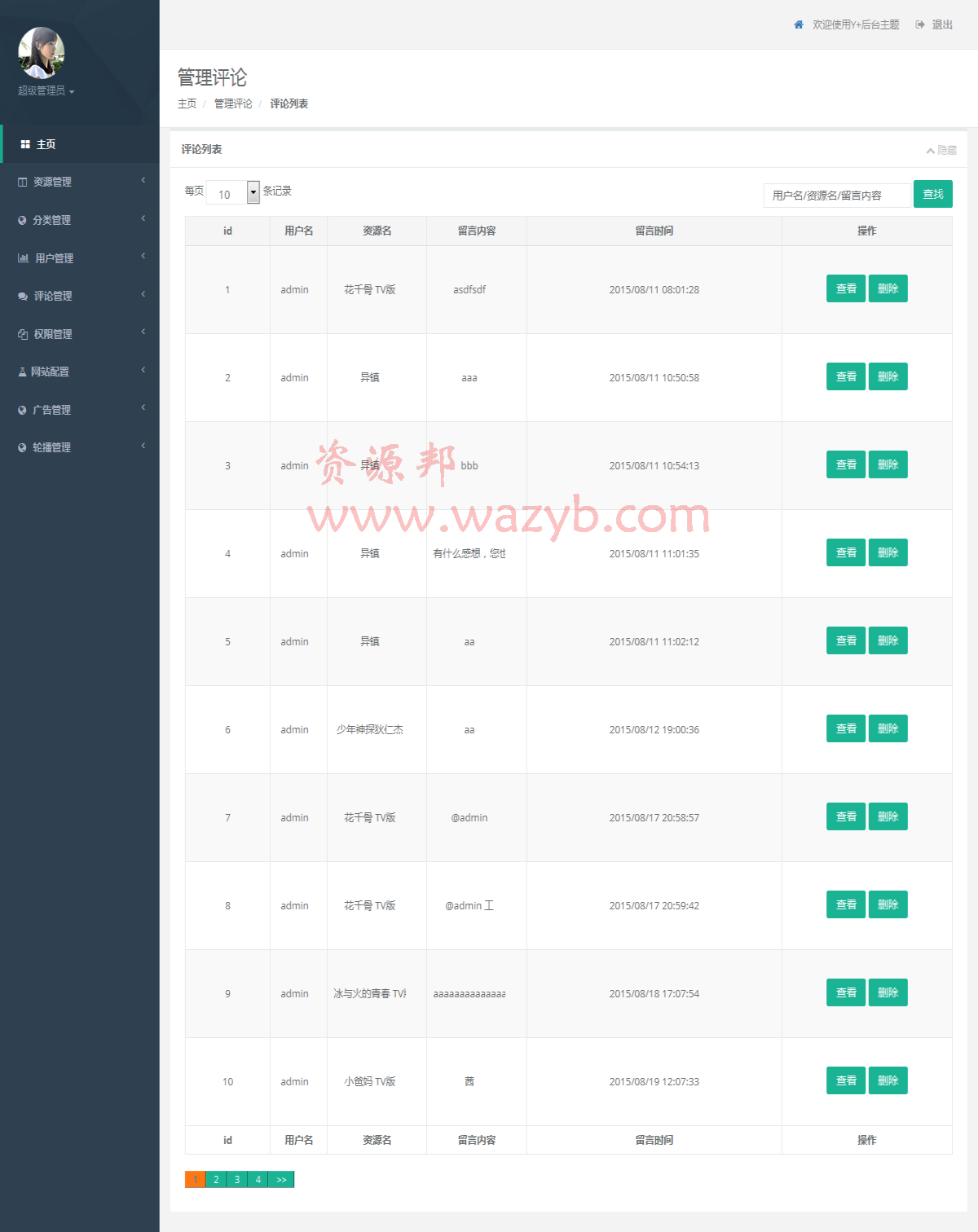
对一个n 边形划分三角问题中，有（ 1 ）弦： n-3 条（ 2 ）三角形： n-2 个

权函数：

权函数是一个自己定义的函数，也就是给凸多边形上的边和弦定义的代价，你可以将边的权定义为路径，时间，距离等，可以赋予你想要的实际意义，下面的程序中的权函数定义的是三角形的周长

3.与矩阵连乘的关系

一个表达式的完全加括号方式相应与一颗完全二叉树，称为表达式的语法树

凸n边形的三角划分对应一颗n-1个叶节点的语法树

凸多边形的语法树，以边为节点

矩阵连乘的最优计算问题是凸多边形最优三角划分问题的特殊情况

4.最优子结构性质

• 若凸 (n+1) 边形 P={V0,V1…… Vn } 的最优三角剖分 T 包含三角形 V0VkVn,1<=k<=n ，

• 则 T 的权为三个部分权之和：三角形 V0VkVn 的权，多边形 {V0,V1…… Vk } 的权和多边形

{Vk,Vk+1…… Vn } 的权之和。

• 可以断言，由 T 确定的这两个子多边形的三角剖分也是最优的。

• 因为若有 {V0,V1…… Vk } 和 {V0,V1…… Vk } 更小权的三角剖分，将导致 T 不是最优三角剖分的矛

盾。因此，凸多边形的三角剖分问题具有最优子结构性质。

5.递归结构

先来看矩阵连乘的递归结构

矩阵连乘分为左半边+右半边+合并时间

而多边形分割的递归结构如下：

可以看到这两个递归结构十分相似

6.代码实现

package 凸多边形最优三角分割;import java.util.Scanner;public class minWeightTriangulation {public static void main(String[] args) {Scanner in = new Scanner(System.in);System.out.println("几边形？");int n = in.nextInt();int[][] n1 = new int[n][n];int[][] m = new int[n][n];int[][] s = new int[n][n];shuzu(n, n1);minWeightTriangulation(n-1, m, s, n1);System.out.println("最优值");shuchu(m);System.out.println("最优解");shuchu(s);System.out.println("划分点");Traceback(1,n-1,s);}//p为边数，n为存储权值的二维数组public static void shuzu(int p, int[][] n) {Scanner in = new Scanner(System.in);//初始化对角线for (int i = 0; i < p; i++)for (int i1 = 0; i1 < p; i1++)n[i][i1] = 0;for (int i = 0; i < p - 1; i++) {for (int l = i + 1; l < p; l++) {System.out.print(i + "点到" + l + "点，边的权值为：");n[i][l] = in.nextInt();}}System.out.println("\n测试输出\n");shuchu(n);}public static void shuchu(int[][] n) {/*测试输出*/for (int i = 0; i < n.length; i++) {for (int l = 0; l < n.length; l++) {System.out.printf("%-8d%s",n[i][l] , " ");}System.out.println();}}public static void minWeightTriangulation(int n, int[][] m, int[][] s, int[][] q) {for (int i = 1; i <= n; i++) {m[i][i] = 0;}//        m最优值，s最优解  w权函数for (int r = 2; r <= n; r++) {//i与j的差值for (int i = 1; i <= n - r + 1; i++) {int j = i + r - 1;m[i][j] = m[i + 1][j] + w(i - 1, i, j, q);//k==i的情况s[i][j] = i;for (int k = i + 1; k < i + r - 1; k++) {int u = m[i][k] + m[k + 1][j] + w(i - 1, k, j, q);if (u < m[i][j]) {m[i][j] = u;s[i][j] = k;}}}}}//    权值函数private static int w(int a, int b, int c, int[][] n) {int num = n[a][b] + n[b][c] + n[a][c];return num;}/*递归倒退函数*/public static void Traceback(int i, int j, int[][] s) {if (i == j) {return;}//子问题的K值Traceback(i, s[i][j], s);Traceback(s[i][j] + 1, j, s);System.out.println("剖分点:" + (i - 1) + " " + j + " " + s[i][j]);}}

7.测试

输入边的权值，之后根据划分点写出分割的多边形，再去计算权值之和，看是否和程序输出的最优值相等

输入：