描述

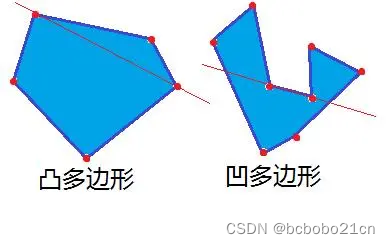
给出平面上n个点的坐标，计算最远两点间的距离，以及包含所有点的最小凸多边形（凸包）

输入
第一行一个整数n，接下来是n行的实数对，表示n个点坐标。2<=n<=10000
n
x1 y1
x2 y2
…
xn yn

输出
输出2行，第一行是最远两点间的距离，结果保留四位小数。第二行是从P0开始，逆时针输出凸包的顶点号。

顶点号为0到n-1，由点的输入次序决定。

P0点表示最下方的点号，如果有多个点并列最下方，则P0为其中最左边的点号。

输入样例 1

9
200 400
300 400
300 300
400 300
400 400
500 400
500 200
350 200
200 200

输出样例 1
360.5551
8 6 5 0

这里用于sort排序的数组ord[],用的很巧妙。
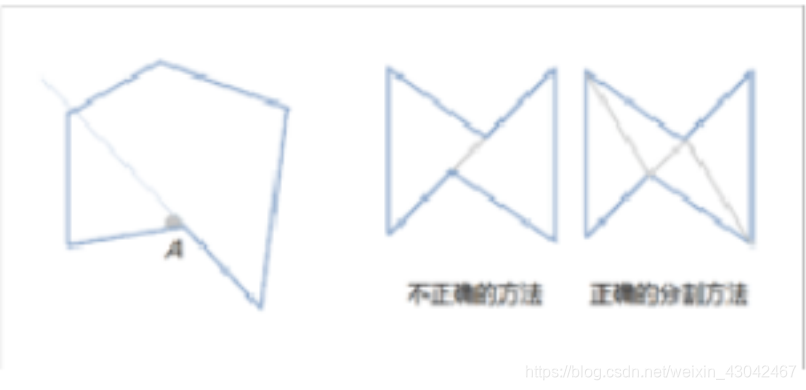
凸包形成过程如下图：

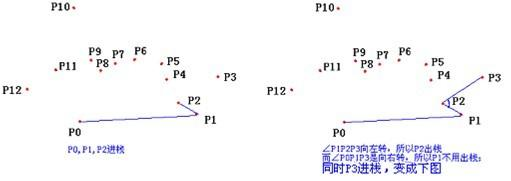
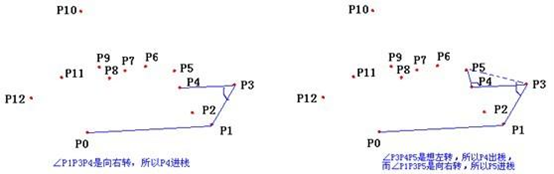
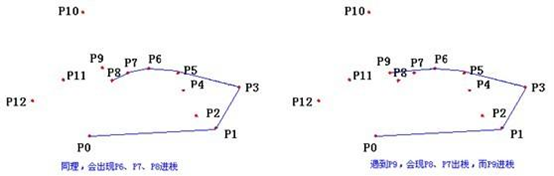
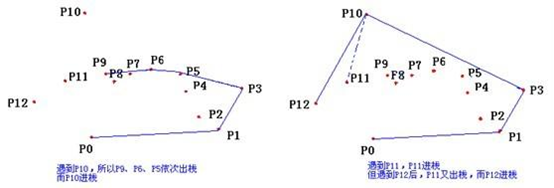
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#define eps 1e-8
using namespace std;
typedef struct
{double x, y;
} point;point p[10005];
//用于排序的标号，并保存输入时的顺序标号 
int ord[10005];
int n;
//stack用于保存最小凸包的顶点序号 
int stack[10005];double dist(point a,point b){return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}int check(point a,point b,point c){double k;k = a.x*b.y-a.y*b.x+b.x*c.y-b.y*c.x+c.x*a.y-c.y*a.x;if(k>eps)return 1;else if(k<-eps)return -1;elsereturn 0;
}bool cmp(int a,int b){//排序依据 int i;i=check(p[ord[0]],p[a],p[b]);if(i==0) return(dist(p[ord[0]],p[a])<dist(p[ord[0]],p[b]));else return i>0;
}int main()
{cin >> n;int i, j,temp;for (i = 0; i < n;i++){cin >> p[i].x >> p[i].y;ord[i] = i;}int k = 0;for (i = 1; i < n;i++){if(p[i].y<p[k].y || (p[i].y==p[k].y && p[i].x<p[k].x))k = i;}swap(ord[0], ord[k]);//将所有点按与水平面夹角大小排序 sort(ord + 1, ord + n, cmp);stack[0] = ord[0];int top=0;for (i = 1; i < n;i++){/*当点p[ord[i]]在线p[stack[top-1]],p[stack[top]]的右边时，链接不构成凸包.所以舍去栈顶的点p[stack[top]]，换成点p[ord[i]]。                    */ while(top>0 && check(p[stack[top-1]],p[stack[top]],p[ord[i]])<=0)  top--;stack[++top] = ord[i];}double ans;for (i = 0; i <= top;i++){//求最长两点距离 for (j = i + 1; j <= top;j++){ans = max(dist(p[stack[i]], p[stack[j]]),ans);}}printf("%.4lf\n", ans);for (i = 0; i <= top; i++)cout << stack[i] << " ";return 0;
}