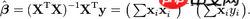线性回归（上）Linear Regression

引言：看看就行

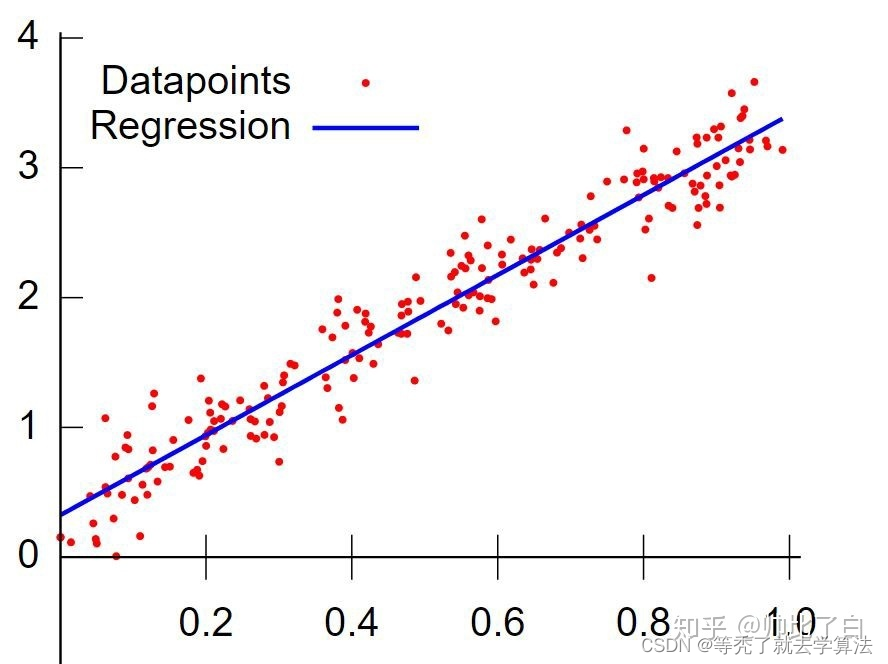
线性回归要做的是就是找到一个数学公式能相对较完美地把所有自变量组合（加减乘除）起来，得到的结果和目标接近

线性回归概念

 机器学习中将如下$R^n->R$的函数$$h_{w,b}=<w,x>+b$$称为一个线性模型。式子中,$w,x\in R^n$均为n维向量，$b\in R$为偏执项。$<w,x>$表示$w$与$x$的内积。
用线性模型来拟合特征组与标签之间的关系的方法，就称为线性回归
 有监督的学习中，求解线性回归模型中的参数$w，b$问题称为线性回归问题。

算法求解步骤

Part1.建立模型基本形式

数据集一共有$p$个数据点，每个数据点有$n$个描述的维度$x_i=(x_{i1},x_{i2},x_{i3},...,x_{in})$ 其中$x_i$是第$i$个数据点。线性模型试图学习到一个通过属性的线性组合来进行预测的函数

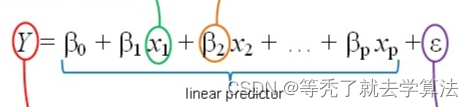
一般用向量形式写成$f(x)=<X,W>+b$其中 $W=(W_1,W_2,W_3,...,W_n)$ ,在 $W$ 和 $b$ 学得之后模型就可以得到确定，所以下一步就是学习模型参数

Part2.选定距离衡量方程

我们的目标：模型预测出来的值和真实值无限接近，即:$f(x_i)\backsimeq y_i$

这里解释一下为什么只能无限接近，因为我们只能拿某一类事件所有数据中抽样出来的部分数据进行学习，抽样出来数据不可能涵盖事件所有的可能性，所以最终只能学习到总体的规律

问题：如何衡量预测的准确性，即衡量 $f(x)$与真实值 $y$之间的差异$$D=E(f(x)-y{)}^2$$

1.误差平方和SSE判别(线性回归就采取这个)$$dist(P_i,P_j)=\sum _{k=1}^n(P_{ik}-P_{jk}{)}^2$$解释：由于误差有正有负，故可以用方法和来抵消正负。
其他的还有欧式距离判别、曼哈顿距离判别、马氏距离判别、等等

Part3.学习模型参数

为简化算法描述中的记号，将n维向量x的首位之前增补一个常数1,使其成为一个$n+1$维向量 $x=(1,x)=(1,x_1,x_2,...,x_n)$
$b$被吸收到$w$向量,$w=(w_0,w_1,...,w_n)$，$b$对应$w_0$。$$Y=<W,X>$$
所以有了如下一图：

这样，我们只需要求解这个方程就能得到$w$和$b$的值。
首先，我们先将方程用矩阵表示：$$Cost(W)=\frac{1}{2m}(XW-Y{)}^T(XW-Y)$$求最小，可以将两边对W求偏导，化简得到方程，令其为零，j解其方程就可以得到W。具体求解过程：详解正规方程$$W=(X^{T}X{)}^{-1}{X}^{T}Y$$

评价指标：$...R^2$

模型建好了，我们需要设计相关的指标来检验模型的表现。有人会问，最小二乘法不就是评价指标吗，和这里的评价指标有什么区别？

从概念上讲，两者都是评价指标没什么区别。但是从使用场景上讲，我们在上文提到的最小二乘法，是我们在用训练数据集训练建模时，为了调整模型参数而确定的评价指标，目的是为了优化模型参数。而这里我们要讲的评价指标，是衡量模型建立好以后，使用别的数据集时（测试数据集、真实数据集）这组模型参数的表现效果，目的是为了选择模型参数

这里给出准确定义：评价指标是针对将相同的数据，输入不同的算法模型，或者输入不同参数的同一种算法模型，而给出这个算法或者参数好坏的定量指标

1.均方误差（SSE）
略
2.均方误差根（标准误差RMSE）
略
3.平方绝对误差（MAE）
略
4.R-square（决定系数）
 对于回归类算法而言，只探索数据预测是否准确是不足够的。除了数据本身的数值大小之外，我们还希望模型能够捕捉到数据的”规律“，比如数据的分布规律，单调性等等，而是否捕获了这些信息并无法使用MSE或者MAE来衡量

数学理解：分母理解为原始数据的离散程度，分子为预测数据和原始数据的误差，二者相除可以消除原始数据离散程度的影响
$$R^2=1-\frac{\sum ({\hat{y}}^{(i)}-y^{(i)})}{\sum (\bar{y}-y^{(i)})}$$

• 上面分子就是我们训练出的模型预测的误差和
• 下面分母就是瞎猜的误差和。（通常取观测值的平均值）
• 如果结果是0，就说明我们的模型跟瞎猜差不多
• 如果结果是1。就说明我们模型无错误
• 介于0~1之间，越接近1，回归拟合效果越好，一般认为超过0.8的模型拟合优度比较高

ps：

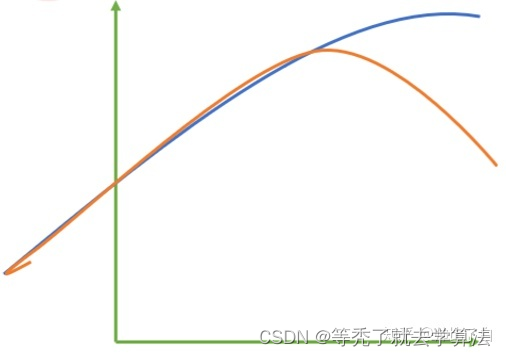
其中红色线是我们的真实标签，而蓝色线是我们的拟合模型。这是一种比较极端，但的确可能发生的情况。这张图前半部分的拟合非常成功，看上去真实标签和预测结果几乎重合，但后半部分的拟合却非常糟糕，模型向着与真实标签完全相反的方向去了

对于这样的一个拟合模型，如果我们使用MSE来对它
进行判断，它的MSE会很小，因为大部分样本其实都被完美拟合了，少数样本的真实值和预测值的巨大差异在被均分到每个样本上之后，MSE就会很小。但这样的拟合结果必然不是一个好结果，因为一旦新样本是处于拟合曲线的后半段的，预测结果必然会有巨大的偏差。所以，我们希望找到新的指标，除了判断预测的数值是否正确之外，还能够判断我们的模型是否拟合了足够多的，数值之外的信息

线性回归（下）Linear Regression

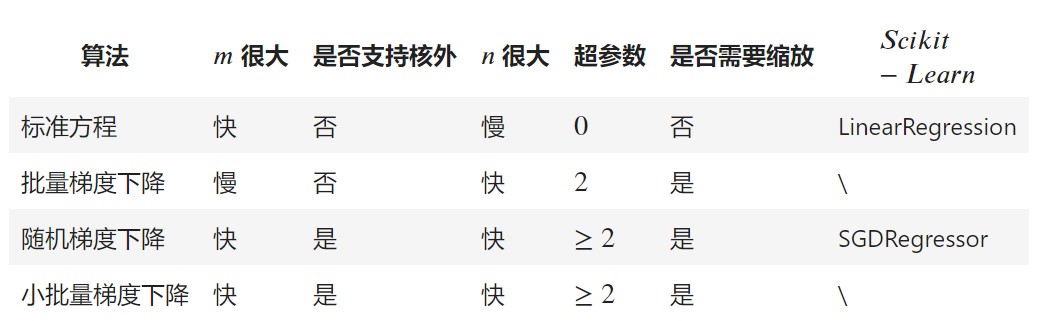
正规方程（最小二乘法）的局限性

• 只有$X^{T}X$可逆时，定理才成立，才有形式简单的解
  $$W=(X^{T}X{)}^{-1}{X}^{T}Y$$
  以下两种情况下，$X^{T}X$都不可逆

  • 所选特征之间不独立，也就是特征之间有联系（$x_1=a{x}_2等关系$）
  • 训练数据个数$m<$特征数$n（m,n=X.shape$ & $m<n）$

• 时间复杂度高

  • $X^{T}X,n$阶方阵，计算$(X^{T}X{)}^{-1}$的时间复杂度$O(n^3)$,公式($A^{-1}=\frac{A\ast }{|A|}$),这对特征数n很大问题，不可接受

多项式回归

• 问题:
   如果特征与标签之间的关系近似线性关系，就可以用一个线性模型来拟合这种回归关系，该拟合方法就是线性回归方法。但是，有些实际问题中，标签与特征之间的关系并非是线性的，而是呈多项式关系。在这种情形下，标签与特征之间的关系就称为多项式关系。如何拟合？
• 解决方法:
   用线性回归的一个变型----多项式回归来拟合标签和特征的关系
  以一个一元二次多项式引入:
  $$h_w(x)=w_0+w_{1}x+w_2{x}^2$$
   只有一个特征$x$，包含3个单项式。
   如果把每一个单项式看成是一个特征，即如果把$1,x,x^2$均看成特征，则上面的一元二次多项式，也可以看作关于这3个特征的线性模型。$$h_w(x)=<w,x>$$$$x=(1,x,x^2)$$$$w=(w_0,w_1,w_2)$$

ps:多项式回归，$x$的首位已经是$1$

一个n元d次多项式:

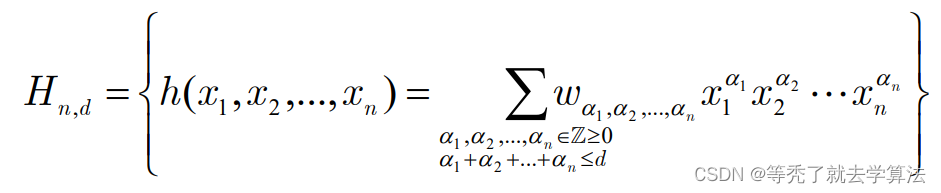
那么，如何确定单项式的个数呢？$$：n元d次多项式含有\left({}_n^{n+d}\right)个单项式$$
每个单项式$x_1^{a_1}{x}_2^{a_2}...x_n^{a_n}$看作一个特征，则一个n元d次多项式模型可以看作一个$\left({}_n^{n+d}\right)$元线性模型

n元d次多项式转$\left({}_n^{n+d}\right)$元线性模型例题

---

---

实例：

1 import numpy as np
2 from sklearn.preprocessing import PolynomialFeatures
3 from machine_learning.linear_regression.lib.linear_regression import LinearRegression
4 import matplotlib.pyplot as plt
5
6 def generate_samples(m):
7 X = 2 * np.random.rand(m, 1) # 样本空间[0,2], X m*1矩阵
8 y = X**2 – 2 * X + 1 + np.random.normal(0, 0.1, (m, 1)) #标签y m*1列向量
9 return X, y
10
11 np.random.seed(0)
12 X, y = generate_samples(100)
13 poly = PolynomialFeatures(degree=2) #声明2次多项式化 实例
14 X_poly = poly.fit_transform(X) #将X 2次多项式化
15 model = LinearRegression() #声明 线性回归模型 实例
16 model.fit(X_poly, y) #训练 线性回归模型
17 print(model.w) #输出模型参数w
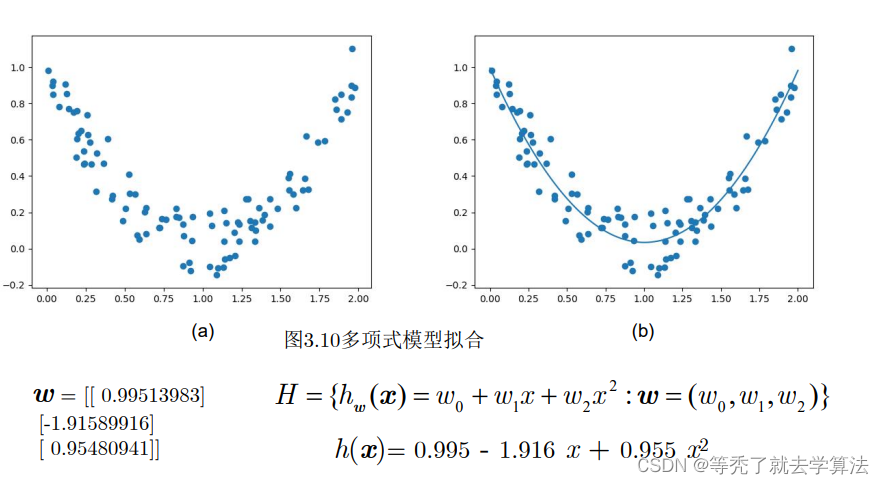
18 plt.scatter(X, y) #画训练数据的散点图
19 X_test = np.linspace(0, 2, 300).reshape(300, 1) #生成 [0,2]之间300个测试数据
20 X_test_poly = poly.fit_transform(X_test) #将X_test 2次多项式化
21 y_pred = model.predict(X_test_poly) #测试
22 plt.plot(X_test, y_pred) #画 300个数据的标签的连线，构成模型的函数图像
23 plt.show(

岭回归

• 问题:

  • 过度拟合

• 解决方式:

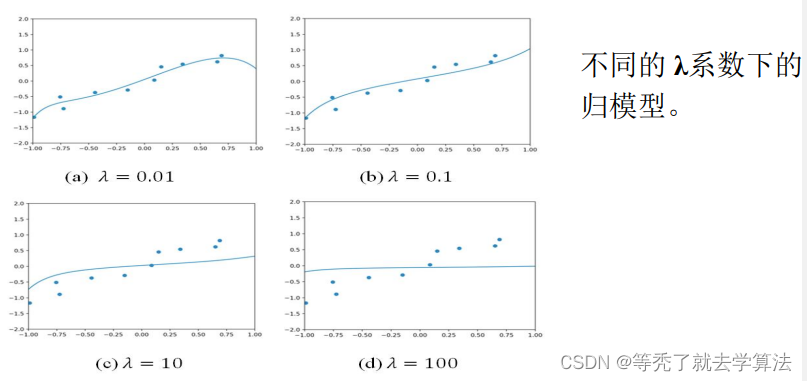
  • 岭回归（在目标函数后追加惩罚）

  $$F(w)=\frac{1}{m}||Xw-y|{|}^2+\lambda ||w|{|}^2$$由此可知，岭回归有唯一解$w^{\ast }$,且$X^{T}X+m\lambda I$可逆时，从而$$w^{\ast }==(X^{T}X+m\lambda I{)}^{-1}{X}^{T}y$$

1 import numpy as np
2
3 class RidgeRegression: #岭回归 线性回归的L2正则化模型
4 def __init__(self, Lambda): #正则化系数λ
5 self.Lambda = Lambda
6
7 def fit(self, X, y): #训练
8 m, n = X.shape
9 r = m * np.diag(self.Lambda * np.ones(n)) # mλI , r=n*n矩阵，对角线上元素值为 mλ
10 self.w = np.linalg.inv(X.T.dot(X) + r).dot(X.T).dot(y) #定理3.3 w* 计算
11
12 def predict(self, X): #预测
13 return X.dot(self.w