SnowFlake 雪花算法详解与实现

我是陈皮，一个在互联网 Coding 的 ITer，个人微信公众号「陈皮的JavaLib」关注第一时间阅读最新文章。

文章目录

- 背景
- SnowFlake 雪花算法
- 算法实现
- 算法验证
- 算法优缺点
- 注意事项

背景

现在的服务基本是分布式，微服务形式的，而且大数据量也导致分库分表的产生，对于水平分表就需要保证表中 id 的全局唯一性。

对于 MySQL 而言，一个表中的主键 id 一般使用自增的方式，但是如果进行水平分表之后，多个表中会生成重复的 id 值。那么如何保证水平分表后的多张表中的 id 是全局唯一性的呢？

如果还是借助数据库主键自增的形式，那么可以让不同表初始化一个不同的初始值，然后按指定的步长进行自增。例如有3张拆分表，初始主键值为1，2，3，自增步长为3。

当然也有人使用 UUID 来作为主键，但是 UUID 生成的是一个无序的字符串，对于 MySQL 推荐使用增长的数值类型值作为主键来说不适合。

也可以使用 Redis 的自增原子性来生成唯一 id，但是这种方式业内比较少用。

当然还有其他解决方案，不同互联网公司也有自己内部的实现方案。雪花算法是其中一个用于解决分布式 id 的高效方案，也是许多互联网公司在推荐使用的。

SnowFlake 雪花算法

SnowFlake 中文意思为雪花，故称为雪花算法。最早是 Twitter 公司在其内部用于分布式环境下生成唯一 ID。在2014年开源 scala 语言版本。

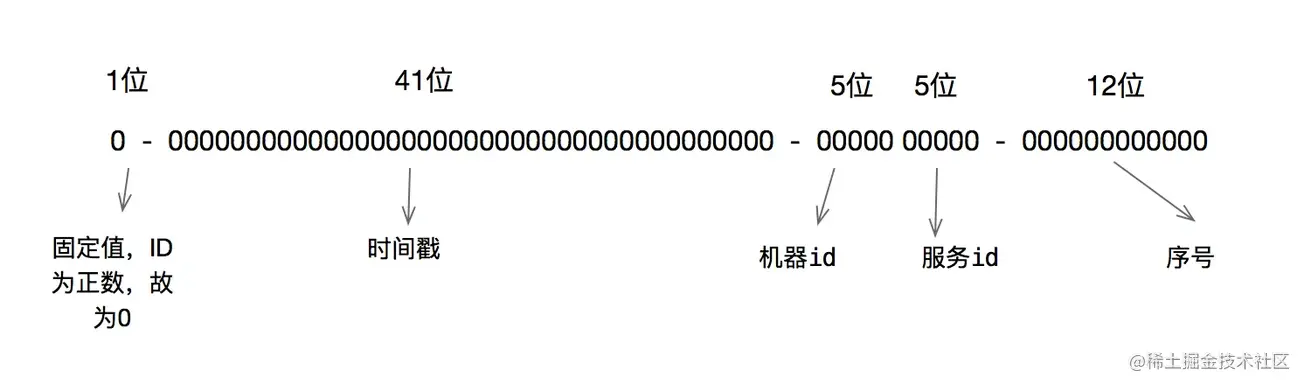
雪花算法原理就是生成一个的64位比特位的 long 类型的唯一 id。

最高1位固定值0，因为生成的 id 是正整数，如果是1就是负数了。
接下来41位存储毫秒级时间戳，2^41/(1000606024365)=69，大概可以使用69年。
再接下10位存储机器码，包括5位 datacenterId 和5位 workerId。最多可以部署2^10=1024台机器。
最后12位存储序列号。同一毫秒时间戳时，通过这个递增的序列号来区分。即对于同一台机器而言，同一毫秒时间戳下，可以生成2^12=4096个不重复 id。

可以将雪花算法作为一个单独的服务进行部署，然后需要全局唯一 id 的系统，请求雪花算法服务获取 id 即可。

对于每一个雪花算法服务，需要先指定10位的机器码，这个根据自身业务进行设定即可。例如机房号+机器号，机器号+服务号，或者是其他可区别标识的10位比特位的整数值都行。

算法实现

package com.chenpi;import java.util.Set;
import java.util.TreeSet;/*** @author 陈皮* @version 1.0* @description 雪花算法ID生成器* @date 2022/4/3*/
public class SnowflakeIdGenerator {// 初始时间戳(纪年)，可用雪花算法服务上线时间戳的值// 1649059688068：2022-04-04 16:08:08private static final long INIT_EPOCH = 1649059688068L;// 记录最后使用的毫秒时间戳，主要用于判断是否同一毫秒，以及用于服务器时钟回拨判断private long lastTimeMillis = -1L;// dataCenterId占用的位数private static final long DATA_CENTER_ID_BITS = 5L;// dataCenterId占用5个比特位，最大值31// 0000000000000000000000000000000000000000000000000000000000011111private static final long MAX_DATA_CENTER_ID = ~(-1L << DATA_CENTER_ID_BITS);// datacenterIdprivate long datacenterId;// workId占用的位数private static final long WORKER_ID_BITS = 5L;// workId占用5个比特位，最大值31// 0000000000000000000000000000000000000000000000000000000000011111private static final long MAX_WORKER_ID = ~(-1L << WORKER_ID_BITS);// workIdprivate long workerId;// 最后12位，代表每毫秒内可产生最大序列号，即 2^12 - 1 = 4095private static final long SEQUENCE_BITS = 12L;// 掩码（最低12位为1，高位都为0），主要用于与自增后的序列号进行位与，如果值为0，则代表自增后的序列号超过了4095// 0000000000000000000000000000000000000000000000000000111111111111private static final long SEQUENCE_MASK = ~(-1L << SEQUENCE_BITS);// 同一毫秒内的最新序号，最大值可为 2^12 - 1 = 4095private long sequence;// workId位需要左移的位数 12private static final long WORK_ID_SHIFT = SEQUENCE_BITS;// dataCenterId位需要左移的位数 12+5private static final long DATA_CENTER_ID_SHIFT = SEQUENCE_BITS + WORKER_ID_BITS;// 时间戳需要左移的位数 12+5+5private static final long TIMESTAMP_SHIFT = SEQUENCE_BITS + WORKER_ID_BITS + DATA_CENTER_ID_BITS;public SnowflakeIdGenerator(long datacenterId, long workerId) {// 检查datacenterId的合法值if (datacenterId < 0 || datacenterId > MAX_DATA_CENTER_ID) {throw new IllegalArgumentException(String.format("datacenterId值必须大于0并且小于%d", MAX_DATA_CENTER_ID));}// 检查workId的合法值if (workerId < 0 || workerId > MAX_WORKER_ID) {throw new IllegalArgumentException(String.format("workId值必须大于0并且小于%d", MAX_WORKER_ID));}this.workerId = workerId;this.datacenterId = datacenterId;}/*** 通过雪花算法生成下一个id，注意这里使用synchronized同步** @return 唯一id*/public synchronized long nextId() {long currentTimeMillis = System.currentTimeMillis();// 当前时间小于上一次生成id使用的时间，可能出现服务器时钟回拨问题if (currentTimeMillis < lastTimeMillis) {throw new RuntimeException(String.format("可能出现服务器时钟回拨问题，请检查服务器时间。当前服务器时间戳：%d，上一次使用时间戳：%d", currentTimeMillis,lastTimeMillis));}if (currentTimeMillis == lastTimeMillis) { // 还是在同一毫秒内，则将序列号递增1，序列号最大值为4095// 序列号的最大值是4095，使用掩码（最低12位为1，高位都为0）进行位与运行后如果值为0，则自增后的序列号超过了4095// 那么就使用新的时间戳sequence = (sequence + 1) & SEQUENCE_MASK;if (sequence == 0) {currentTimeMillis = tilNextMillis(lastTimeMillis);}} else { // 不在同一毫秒内，则序列号重新从0开始，序列号最大值为4095sequence = 0;}// 记录最后一次使用的毫秒时间戳lastTimeMillis = currentTimeMillis;// 核心算法，将不同部分的数值移动到指定的位置，然后进行或运行return ((currentTimeMillis - INIT_EPOCH) << TIMESTAMP_SHIFT) | (datacenterId<< DATA_CENTER_ID_SHIFT) | (workerId << WORK_ID_SHIFT) | sequence;}/*** 获取指定时间戳的接下来的时间戳，也可以说是下一毫秒** @param lastTimeMillis 指定毫秒时间戳* @return 时间戳*/private long tilNextMillis(long lastTimeMillis) {long currentTimeMillis = System.currentTimeMillis();while (currentTimeMillis <= lastTimeMillis) {currentTimeMillis = System.currentTimeMillis();}return currentTimeMillis;}public static void main(String[] args) {SnowflakeIdGenerator snowflakeIdGenerator = new SnowflakeIdGenerator(1, 2);// 生成50个idSet<Long> set = new TreeSet<>();for (int i = 0; i < 50; i++) {set.add(snowflakeIdGenerator.nextId());}System.out.println(set.size());System.out.println(set);// 验证生成100万个id需要多久long startTime = System.currentTimeMillis();for (int i = 0; i < 1000000; i++) {snowflakeIdGenerator.nextId();}System.out.println(System.currentTimeMillis() - startTime);}
}

算法验证

public static void main(String[] args) {SnowflakeIdGenerator snowflakeIdGenerator = new SnowflakeIdGenerator(1, 2);// 生成50个idSet<Long> set = new TreeSet<>();for (int i = 0; i < 50; i++) {set.add(snowflakeIdGenerator.nextId());}System.out.println(set.size());System.out.println(set);// 验证生成100万个id需要多久long startTime = System.currentTimeMillis();for (int i = 0; i < 1000000; i++) {snowflakeIdGenerator.nextId();}System.out.println(System.currentTimeMillis() - startTime);}

在我的笔记本，测试结果如下，生成的50个id是不重复的，而且 id 值是递增的。然后再测试生成100万个 id，只花费了262毫秒，可见是算法是及其高效的。

50
[268133605376, 268133605377, 268133605378, 268133605379, 268133605380, 268133605381, 268133605382, 268133605383, 268133605384, 268133605385, 268133605386, 268133605387, 268133605388, 268133605389, 268133605390, 268133605391, 268133605392, 268133605393, 268133605394, 268133605395, 268133605396, 268133605397, 268133605398, 268133605399, 268133605400, 268133605401, 268133605402, 268133605403, 268133605404, 268133605405, 268133605406, 268133605407, 268133605408, 268133605409, 268133605410, 268133605411, 268133605412, 268133605413, 268133605414, 268133605415, 268133605416, 268133605417, 268133605418, 268133605419, 268133605420, 268133605421, 268133605422, 268133605423, 268133605424, 268133605425]
262