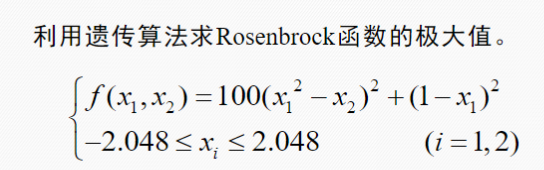遗传算法（基础知识）

遗传算法简称GA（Genetic Algorithms）模拟自然界生物遗传学（孟德尔）和生物进化论（达尔文）通过人工方式所构造的一类 并行随机搜索最优化方法，是对生物进化过程**“优胜劣汰，适者生存”**这一过程进行的一种数学仿真

一、主要思想

遗传算法是根据达尔文的“适者生存，优胜劣汰”的思想来找到最优解的，其特点是所找到的解是全局最优解（这点其实后面被推翻，我会再有一个精英保留政策来加强找到全局最优解的能力），相对于蚁群算法可能出现的局部最优解还是有优势的

二、算法简介

• 个体（染色体）：一个染色体代表一个具体问题的一个解，一个染色体包含若干基因。
• 基因：一个基因代表具体问题解的一个决策变量。
• 种群：多个个体（染色体）构成一个种群。即一个问题的多组解构成了解的种群

我们的目的就是让种群中”优胜劣汰“，最终只剩下一个最优解。接下来介绍最基本遗传算法，只用了选择，交叉，变异三种遗传算子。

遗传算法将“优胜劣汰，适者生存”的生物进化原理引入优化参数形成的编码串群体中，按所选择的适应度函数并通过遗传中的复制、交叉及变异对个体进行筛选，适应度高的个体被保留下来，组成新的群体，新的群体既继承了上一代的信息，又优于上一代。这样周而复始，群体中个体适应度不断提高，直到满足一定的条件。遗传算法的算法简单，可并行处理，并能到全局最优解。

该算法特点：

1. 智能式搜索
   遗传算法的搜索策略，既不是盲目式的乱搜索，也不是穷举式的全面搜索，它是有指导的搜索。指导遗传算法执行搜索的依据是适应度，也就是它的目标函数。利用适应度，使遗传算法逐步逼近目标值
2. 渐进式优化
   遗传算法利用复制、交换、突变等操作，使新一代的结果优越于旧一代，通过不断迭代，逐渐得出最优的结果，它是一种反复迭代的过程
3. 全局最优解
   遗传算法由于采用交换、突变等操作，产生新的个体，扩大了搜索范围，使得搜索得到的优化结果是全局最优解而不是局部最优解
4. 黑箱式结构
   遗传算法根据所解决问题的特性，进行编码和选择适应度。一旦完成字符串和适应度的表达，其余的复制、交换、突变等操作都可按常规手续执行。个体的编码如同输入，适应度如同输出。因此遗传算法从某种意义上讲是一种只考虑输入与输出关系的黑箱问题
5. 通用性强
   传统的优化算法，需要将所解决的问题用数学式子表示，常常要求解该数学函数的一阶导数或二阶导数。采用遗传算法，只用编码及适应度表示问题，并不要求明确的数学方程及导数表达式。因此，遗传算法通用性强，可应用于离散问题及函数关系不明确的复杂问题，有人称遗传算法是一种框架型算法，它只有一些简单的原则要求，在实施过程中可以赋予更多的含义
6. 并行式算法
   遗传算法是从初始群体出发，经过复制、交换、突变等操作，产生一组新的群体。每次迭代计算，都是针对一组个体同时进行，而不是针对某个个体进行。因此，尽管遗传算法是一种搜索算法，但是由于采用这种并行机理，搜索速度很高。这种并行式计算是遗传算法的一个重要特征

遗传算法主要包括以下三个方面：
（1）遗传：这是生物的普遍特征，亲代把生物信息交给子代，子代总是和亲代具有相同或相似的性状。生物有了这个特征，物种才能稳定存在。
（2）变异：亲代和子代之间以及子代的不同个体之间的差异，称为变异。变异是随机发生的，变异的选择和积累是生命多样性的根源。
（3）生存斗争和适者生存：具有适应性变异的个体被保留下来，不具有适应性变异的个体被淘汰，通过一代代的生存环境的选择作用，性状逐渐逐渐与祖先有所不同，演变为新的物种

三、基本操作

1、选择复制

复制是从一个旧种群中选择生命力强的个体位串产生新种群的过程。具有高适应度的位串更有可能在下一代中产生一个或多个子孙。（从旧种群中选择出优秀者，但不能创造新的染色体）复制操作可以通过随机方法来实现。首先产生0-1之间均匀分布的随机数，若某串的复制概率为40%，则当产生的随机数在0~0.40之间时，该串被复制，否则被淘汰

通过轮盘赌等方式将适应度高的个体从当前种群中选择出来。其中轮盘赌即是与适应度成正比的概率来确定各个个体遗传到下一代群体中的数量。
具体步骤如下：

1. 首先计算出所有个体的适应度总和Σfi。

2. 其次计算出每个个体的相对适应度大小fi/Σfi，类似于softmax。

3. 再产生一个0到1之间的随机数，依据随机数出现在上述哪个概率区域内来确定各个个体被选中的次数。

2、交叉

交叉：交叉模拟了生物进化过程中的繁殖现象，通过两个染色体的交换组合，来产生新的优良品种。交叉体现了自然界中信息交换的思想。交叉有单点交叉、两点交叉、还有一致交叉、顺序交叉和周期交叉。单点交叉是最基本的方法，应用较广。它是指在匹配池中任选两个染色体，随机选择一个交换点位置，交换双亲染色体交换点右边的部分，即可得到两个新的染色体，例：

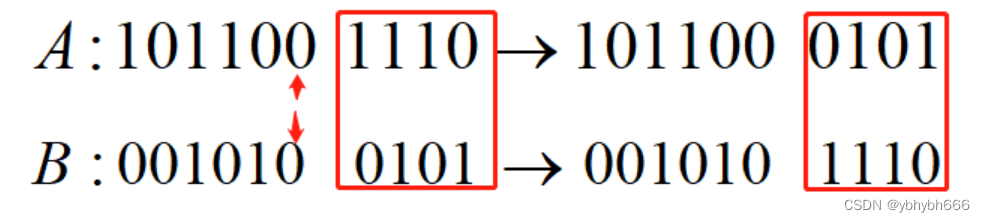
3、变异

变异运算用来模拟生物在自然的遗传环境中由于各种偶然因素引起的基因突变，它以很小的概率随机地改变遗传基因（表示染色体的符号串的某一位）的值。在染色体以二进制编码的系统中，变异表现为随机地将染色体的某一个基因由1变为0，或由0变为1

四、算法流程

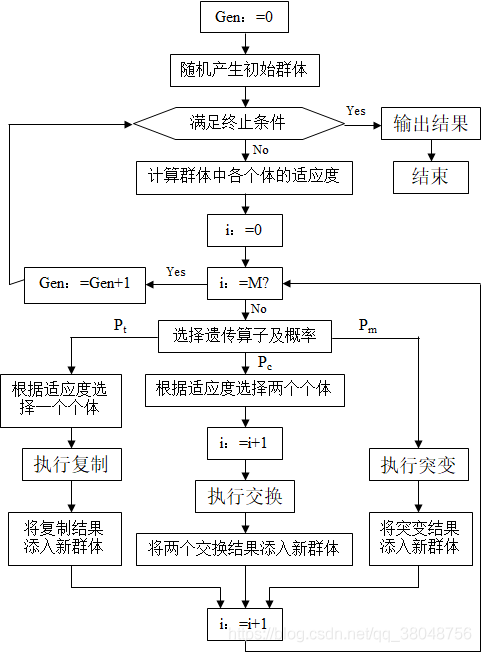
Gen：遗传（迭代）的代次。表明遗传算法反复执行的次数，即已产生群体的代次数目。
M：群体中拥有的个体数目。
i：已处理个体的累计数，当i等于M，表明这一代的个体已全部处理完毕，需要转入下一代群体。

交叉率 Pc就是参加交叉运算的染色体个数占全体染色体总数的比例，记为Pc,取值范围一般为0.4～0.99。
变异率Pm是指发生变异的基因位数所占全体染色体的基因总位数的比例，记为Pm，取值范围一般为0.0001~0.1
复制概率Pt用于控制复制与淘汰的个体数目。

遗传算法主要执行以下四步：

1. 随机地建立由字符串组成的初始群体；

2. 计算各个体的适应度；

3. 根据遗传概率，利用下述操作产生新群体：

   a. 复制。将已有的优良个体复制后添入新群体中，删除劣质个体
   b. 交换。将选出的两个个体进行交换，所产生的新个体添入新群体中
   c.突变。随机地改变某一个体的某个字符后添入新群体中

4. 反复执行上述操作后，一旦达到终止条件，选择最佳个体作为遗传算法的结果

求f(x)=x^2,x属于[0,31] 求其二次函数的最大值

1、编码

遗传算法首先要对实际问题进行编码，用字符串表达问题。这种字符串相当于遗传学中的染色体。每一代所产生的字符串个体总和称为群体。为了实现的方便，通常字符串长度固定，字符选0或1。
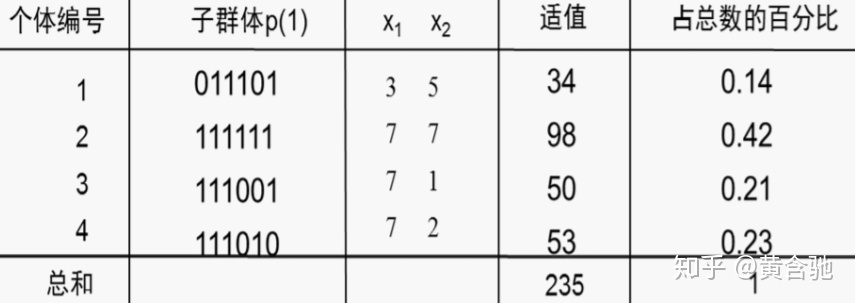
本例中，利用5位二进制数表示x值，采用随机产生的方法，假设得出拥有四个个体的初始群体，即：01101，11000，01000，10011。x值相应为13，24，8，19

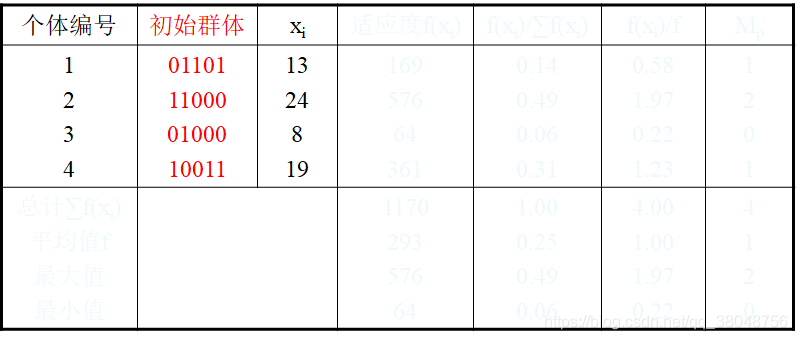
2、计算适应度

衡量字符串（染色体）好坏的指标是适应度，它也就是遗传算法的目标函数。本例中用x^2计算

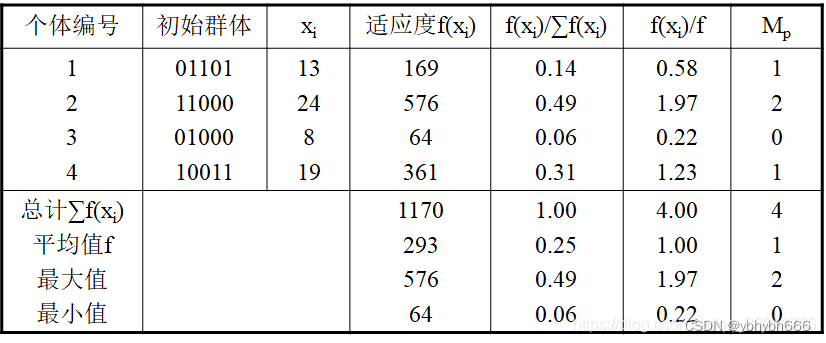
表中第6列的 f(xi)/f 表示每个个体的相对适应度，它反映了个体之间的相对优劣性。如2号个体的 f(xi)/f 值最高（1.97），为优良个体，3号个体最低（0.22），为不良个体

3、复制

根据相对适应度的大小对个体进行取舍，2号个体性能最优，予以复制繁殖。3号个体性能最差，将它删除，使之死亡，表中的M表示传递给下一代的个体数目，其中2号个体占2个，3号个体为0，1号、4号个体保持为1个。这样，就产生了下一代群体

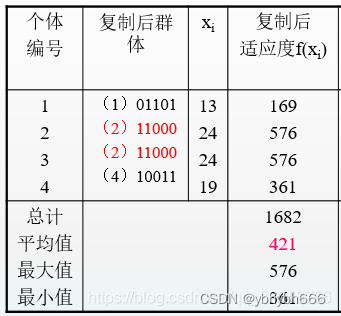
复制后产生的新一代群体的平均适应度明显增加，由原来的293增加到421

4、交换

利用随机配对的方法，决定1号和2号个体、3号和4号个体分别交换，如表中第5列。再利用随机定位的方法，确定这两对母体交叉换位的位置分别从字符长度的第4位及第3位开始。如：3号、4号个体从字符长度第3位开始交换。交换开始的位置称交换点

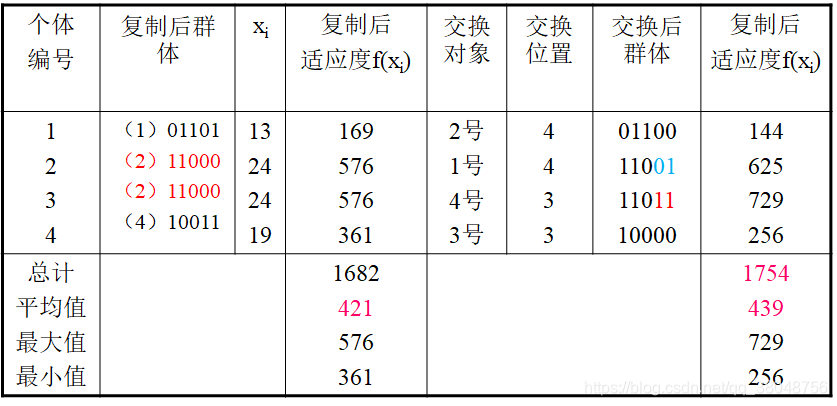
5、突变

将个体字符串某位符号进行逆变，即由1变为0或由0变为1。例如，下式左侧的个体于第3位突变，得到新个体如右侧所示：

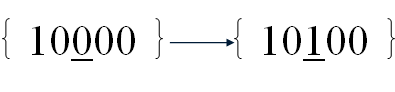
遗传算法中，个体是否进行突变以及在哪个部位突变，都由事先给定的概率决定。通常，突变概率很小，本例的第一代中就没有发生突变。

上述（2）～（5）反复执行，直至得出满意的最优解。

综上可以看出，遗传算法参考生物中有关进化与遗传的过程，利用复制、交换、突变等操作，不断循环执行，逐渐逼近全局最优解。

五、算法实现

1、编码与解码

将不同的实数表示成不同的0，1二进制串表示就完成了编码，因此我们并不需要去了解一个实数对应的二进制具体是多少，我们只需要保证有一个映射能够将十进制的数编码为二进制即可。而在最后我们肯定要将编码后的二进制串转换为我们理解的十进制串，所以我们需要的是y = f ( x )的逆映射，也就是将二进制转化为十进制，也就是解码，十进制与二进制相互映射的关系以下为例进行说明：
例如 ：对于一个长度为10的二进制串,如[0,0,0,1,0,0,0,0,0,1]，将其映射到[1,3]这个区间

另外需要注意的是一个基因可能存储了多个数据的信息，在进行解码时注意将其分开，如一个基因含有x,y两个数据，该基因型的长度为20，可以用前10位表示x，后10位表示y，解码时分开进行解码

2、适应度

在实际问题中，有时希望适应度越大越好（如赢利、劳动生产率），有时要求适应度越小越好（费用、方差）。为了使遗传算法有通用性，这种最大、最小值问题宜统一表达。通常都统一按最大值问题处理，而且不允许适应度小于0

对于最小值问题，其适应度按下式转换：

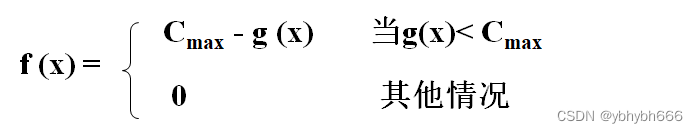
为了保证适应度不出现负值，对于有可能产生负值的最大值问题，可以采用下式进行变换：

3、选择

有了适度函数，然后就可以根据某个基因的适应度函数的值与所有基因适应度的总和的比值作为选择的依据，该值大的个体更易被选择，可以通过有放回的随机采样来模拟选择的过程

4、交叉和变异

交叉和 变异都是随机发生的，对于交叉而言，随机选择其双亲，并随机选择交叉点位，按照一定的概率进行交叉操作。可以通过以下方式实现：首先选择种群中的一个个体作为父亲，然后通过产生一个[0,1]随机数,将其与定义的交叉概率比较，如果小于该数，则在种群中随机选择另外的母亲，随机选择交叉点位进行交叉

5、代码举例

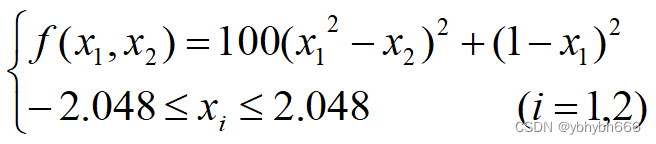
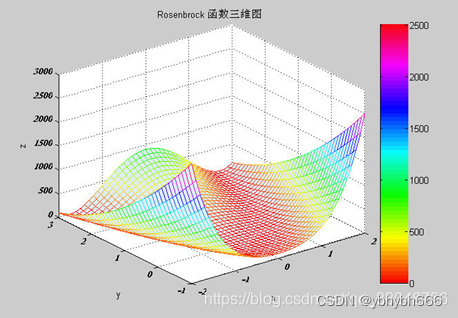
由于该函数的值非负就使用该函数的值作为适应度值

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
DNA_SIZE = 24
POP_SIZE = 80
CROSSOVER_RATE = 0.6  #交叉率
MUTATION_RATE = 0.01   #变异率
N_GENERATIONS = 100   #迭代次数
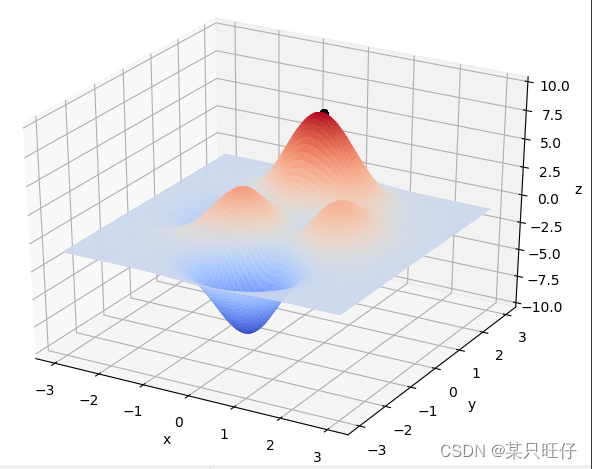
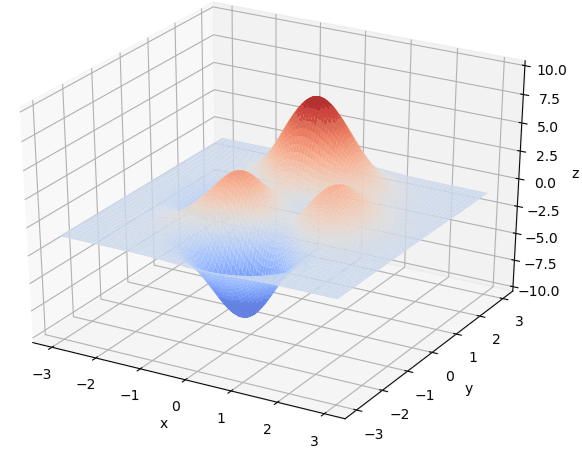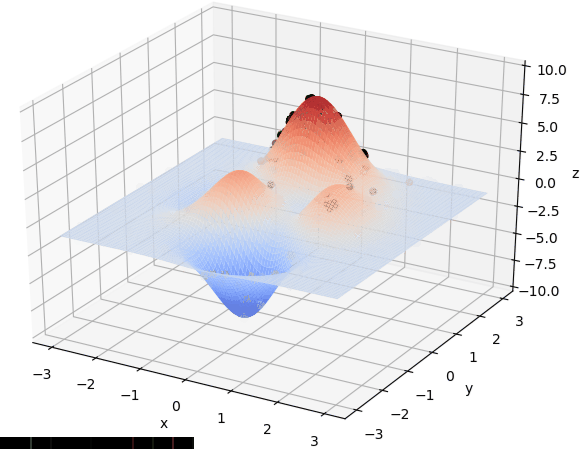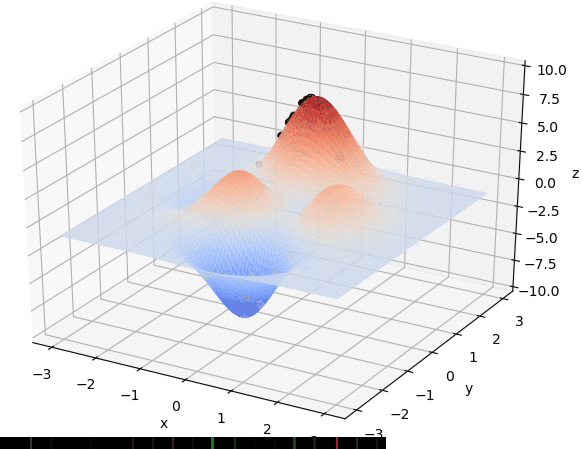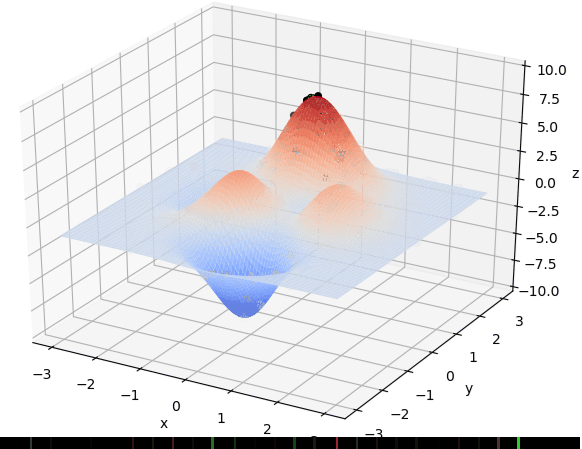
X_BOUND = [-2.048, 2.048]
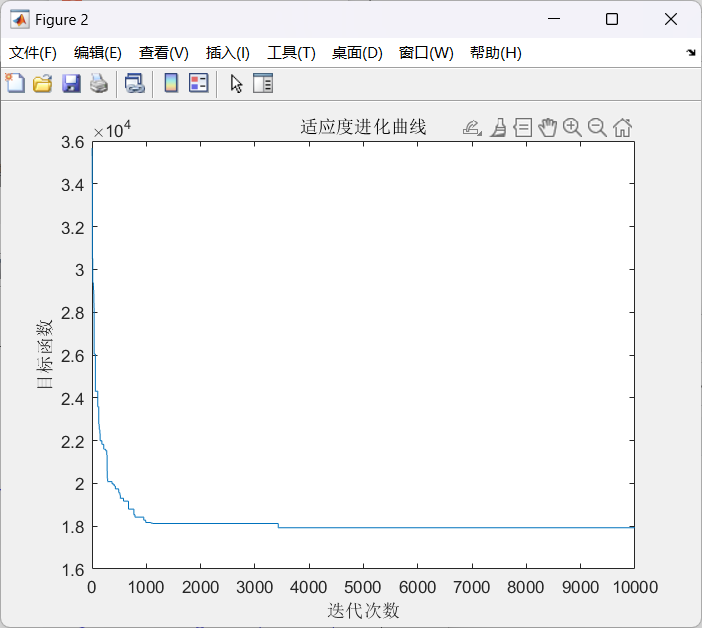
Y_BOUND = [-2.048, 2.048]def F(x, y):return 100.0 * (y - x ** 2.0) ** 2.0 + (1 - x) ** 2.0  # 以香蕉函数为例def plot_3d(ax):X = np.linspace(*X_BOUND, 100)Y = np.linspace(*Y_BOUND, 100)X, Y = np.meshgrid(X, Y)Z = F(X, Y)ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm)ax.set_xlabel('x')ax.set_ylabel('y')ax.set_zlabel('z')plt.pause(3)plt.show()def get_fitness(pop):x, y = translateDNA(pop)pred = F(x, y)return pred# return pred - np.min(pred)+1e-3  # 求最大值时的适应度# return np.max(pred) - pred + 1e-3  # 求最小值时的适应度，通过这一步fitness的范围为[0, np.max(pred)-np.min(pred)]def translateDNA(pop):  # pop表示种群矩阵，一行表示一个二进制编码表示的DNA，矩阵的行数为种群数目x_pop = pop[:, 0:DNA_SIZE]  # 前DNA_SIZE位表示Xy_pop = pop[:, DNA_SIZE:]  # 后DNA_SIZE位表示Yx = x_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (X_BOUND[1] - X_BOUND[0]) + 	X_BOUND[0]y = y_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (Y_BOUND[1] - Y_BOUND[0]) + Y_BOUND[0]return x, ydef crossover_and_mutation(pop, CROSSOVER_RATE=0.8):new_pop = []for father in pop:  # 遍历种群中的每一个个体，将该个体作为父亲child = father  # 孩子先得到父亲的全部基因（这里我把一串二进制串的那些0，1称为基因）if np.random.rand() < CROSSOVER_RATE:  # 产生子代时不是必然发生交叉，而是以一定的概率发生交叉mother = pop[np.random.randint(POP_SIZE)]  # 再种群中选择另一个个体，并将该个体作为母亲cross_points = np.random.randint(low=0, high=DNA_SIZE * 2)  # 随机产生交叉的点child[cross_points:] = mother[cross_points:]  # 孩子得到位于交叉点后的母亲的基因mutation(child)  # 每个后代有一定的机率发生变异new_pop.append(child)return new_popdef mutation(child, MUTATION_RATE=0.003):if np.random.rand() < MUTATION_RATE:  # 以MUTATION_RATE的概率进行变异mutate_point = np.random.randint(0, DNA_SIZE*2)  # 随机产生一个实数，代表要变异基因的位置child[mutate_point] = child[mutate_point] ^ 1  # 将变异点的二进制为反转def select(pop, fitness):  # nature selection wrt pop's fitnessidx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,p=(fitness) / (fitness.sum()))return pop[idx]def print_info(pop):fitness = get_fitness(pop)max_fitness_index = np.argmax(fitness)print("max_fitness:", fitness[max_fitness_index])x, y = translateDNA(pop)print("最优的基因型：", pop[max_fitness_index])print("(x, y):", (x[max_fitness_index], y[max_fitness_index]))print(F(x[max_fitness_index], y[max_fitness_index]))if __name__ == "__main__":fig = plt.figure()ax = Axes3D(fig)plt.ion()  # 将画图模式改为交互模式，程序遇到plt.show不会暂停，而是继续执行plot_3d(ax)pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE * 2))  # matrix (POP_SIZE, DNA_SIZE)for _ in range(N_GENERATIONS):  # 迭代N代x, y = translateDNA(pop)if 'sca' in locals():sca.remove()  #为了方便画图，每一次删除上次种群的点sca = ax.scatter(x, y, F(x, y), c='black', marker='o')plt.show()plt.pause(0.1)pop = np.array(crossover_and_mutation(pop, CROSSOVER_RATE))fitness = get_fitness(pop)pop = select(pop, fitness)  # 选择生成新的种群print_info(pop)plt.ioff()plot_3d(ax)

六、应用场景

1. 函数优化
   函数优化是遗传算法的经典应用领域，也是遗传算法进行性能评价的常用算例。尤其是对非线性、多模型、多目标的函数优化问题，采用其他优化方法较难求解，而遗传算法却可以得到较好的结果
2. 组合优化。
   随着问题的增大，组合优化问题的搜索空间也急剧扩大，采用传统的优化方法很难得到最优解。遗传算法是寻求这种满意解的最佳工具。例如，遗传算法已经在求解旅行商问题、背包问题、装箱问题、图形划分问题等方面得到成功的应用
3. 生产调度问题
   在很多情况下，采用建立数学模型的方法难以对生产调度问题进行精确求解。在现实生产中多采用一些经验进行调度。遗传算法是解决复杂调度问题的有效工具，在单件生产车间调度、流水线生产车间调度、生产规划、任务分配等方面遗传算法都得到了有效的应用
4. 自动控制
   在自动控制领域中有很多与优化相关的问题需要求解，遗传算法已经在其中得到了初步的应用。例如，利用遗传算法进行控制器参数的优化、基于遗传算法的模糊控制规则的学习、基于遗传算法的参数辨识、基于遗传算法的神经网络结构的优化和权值学习等
5. 机器人
   例如，遗传算法已经在移动机器人路径规划、关节机器人运动轨迹规划、机器人结构优化和行为协调等方面得到研究和应用
6. 图像处理
   遗传算法可用于图像处理过程中的扫描、特征提取、图像分割等的优化计算。目前遗传算法已经在模式识别、图像恢复、图像边缘特征提取等方面得到了应用

————————————————
资料来源：CSDN博主「ybhybh666」的原创文章
原文链接：https://blog.csdn.net/abc1234564546/article/details/126184673

CSDN博主「馋学习的身子」的原创文章
原文链接：https://blog.csdn.net/qq_38048756/article/details/109256062