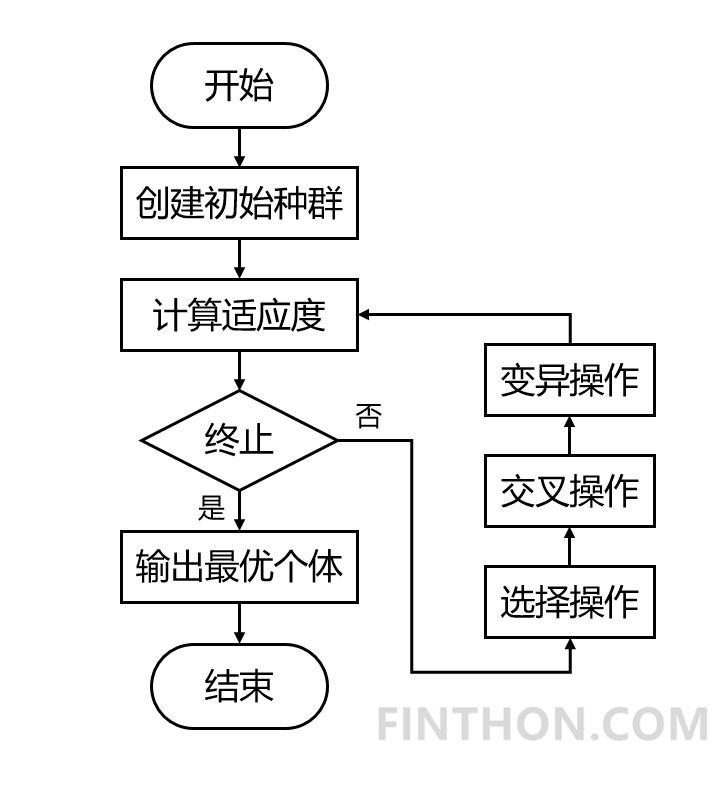
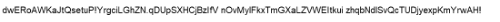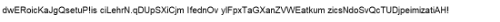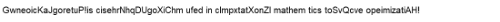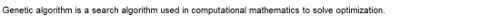遗传算法(Genetic Algorithm)顾名思义,是一种基于自然选择原理和自然遗传机制的启发式搜索算法。该算法通过模拟自然界中生物遗传进化的自然机制(选择、交叉和变异操作),将好的遗传基因(最优目标)不断遗传给子代,使得后代产生最优解的概率增加(后代还是会有一些差的结果)。它的整个算法流程如下:
- 首先根据具体问题确定可行解域和编码方式,用数值串或字符串的形式表示可行解域中的每一个可行解;
- 构建适应度函数度量每一解,该函数为非负函数;
- 确定种群的大小、选择、交叉和变异的方式、交叉和变异的概率,判断终止条件(可以是某一阈值或者是指定进化的代数)。
在这个过程当中,交叉操作是优化的主要操作,而变异操作可以看成对种群的扰动。根据具体的问题我们构建适应度函数,并优化极值(可以是求最大值,也可以求最小值)。
名词解析
生物遗传概念在遗传算法中的对应关系如下:
| 生物遗传概念 | 遗传算法中的作用 |
|---|---|
| 适者生存 | 算法停止时,最优目标值的解大概率被找到 |
| 个体 | 每个可行解 |
| 染色体 | 对每个可行解的编码 |
| 基因 | 可行解中的每个组成部分 |
| 适应性 | 适应度函数的函数值 |
| 种群 | 可行解域,根据适应度函数选择的一组解 |
| 选择 | 保留适应度函数的函数值优的解 |
| 交叉 | 将两个可行解内的组分随机交叉,产生新解 |
| 变异 | 随机变异可行解中的某些组分 |
算法步骤
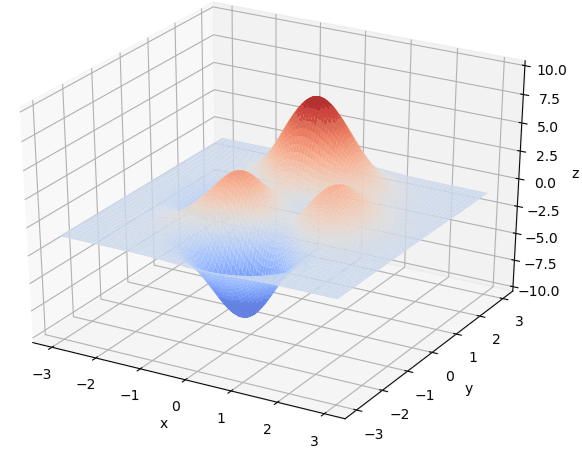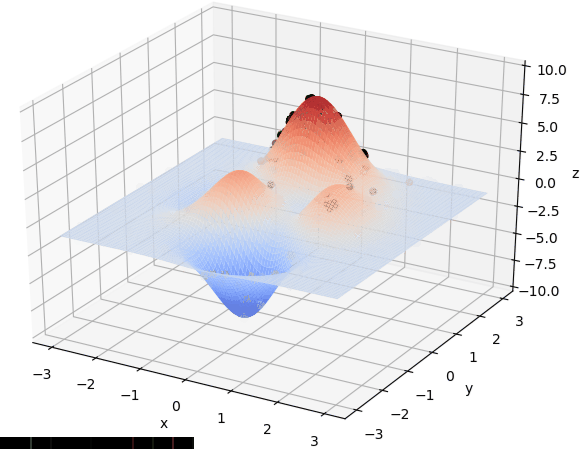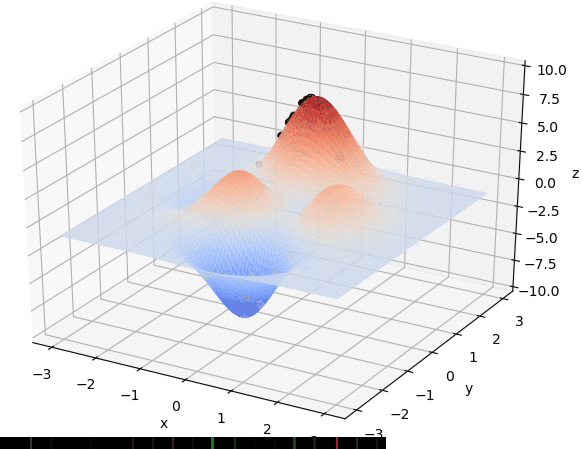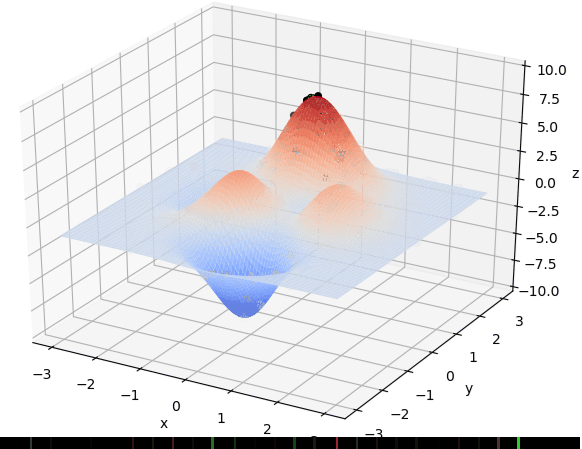
我们还是以一个简单的例子来讲解整个算法的流程。比如,我们需要寻找函数y=x12+x22+x33+x44在[1,30]之间的最大值。我们很容易就知道,当x1=x2=x3=x4=30时,该函数能取到最大值。
首先我们构建一个叫Gene的类:
| 1 2 3 4 | class Gene: def __init__(self, **data): self.__dict__.update(data) self.size = len(data['data']) # length of gene |
这个类只有一个初始化方法,该方法就是获得基因里面的内容和大小,在这个例子中,内容就是[1,30]之间的任意4个数字组成的列表。
接着构建一个叫GA的类,这个类包括算法的所有操作方法:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | class GA: def __init__(self, parameter): pass def evaluate(self, geneinfo): pass def selectBest(self, pop): pass def selection(self, individuals, k): pass def crossoperate(self, offspring): pass def mutation(self, crossoff, bound): pass def GA_main(self): pass |
使用__init__()方法初始化参数,包括自变量可取的最大值,最小值,种群大小,交叉率,变异率和繁殖代数;使用evaluate()方法作为适应度函数评估该个体的函数值,在这里就是函数y的值;使用selectBest()方法挑选出当前代种群中的最好个体作为历史记录;使用selection()方法按照概率从上一代种群中选择个体,直至形成新的一代;使用crossoperate()方法实现交叉操作;使用mutation()方法实现变异操作;使用GA_main()方法实现整个算法的循环。
接下来我们会一一对其进行解析。
__init__()方法
__init__()方法的代码如下:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | def __init__(self, parameter): # parameter = [CXPB, MUTPB, NGEN, popsize, low, up] self.parameter = parameter low = self.parameter[4] up = self.parameter[5] self.bound = [] self.bound.append(low) self.bound.append(up) pop = [] for i in range(self.parameter[3]): geneinfo = [] for pos in range(len(low)): geneinfo.append(random.randint(self.bound[0][pos], self.bound[1][pos])) # initialise popluation fitness = self.evaluate(geneinfo) # evaluate each chromosome pop.append({'Gene': Gene(data=geneinfo), 'fitness': fitness}) # store the chromosome and its fitness self.pop = pop self.bestindividual = self.selectBest(self.pop) # store the best chromosome in the population |
初始化方法接受传入的参数,包括最大值,最小值,种群大小,交叉率,变异率和繁殖代数。通过这些参数随机产生一个种群的列表pop作为首代种群,里面的每一条染色体是一个字典,该字典有两个内容,分别是包含基因的Gene类和适应度函数值fitness。
evaluate()方法
在初始化方法中,要用到适应度函数计算函数值,它的定义如下:
| 1 2 3 4 5 6 7 | def evaluate(self, geneinfo): x1 = geneinfo[0] x2 = geneinfo[1] x3 = geneinfo[2] x4 = geneinfo[3] y = x1**2 + x2**2 + x3**3 + x4**4 return y |
selectBest()方法
在初始化方法中,需要先将首代中最好的个体保留作为记录,它的定义如下:
| 1 2 3 | def selectBest(self, pop): s_inds = sorted(pop, key=itemgetter("fitness"), reverse=True) # from large to small, return a pop return s_inds[0] |
对整个种群按照适应度函数从大到小排序,返回最大值的个体。
selection()方法
按照概率从上一代种群中选择个体,直至形成新的一代。我们需要适应度函数值大的个体被选择的概率大,可以使用轮盘赌选择法。该方法的步骤如下:

它的代码实现如下:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | def selection(self, individuals, k): s_inds = sorted(individuals, key=itemgetter("fitness"), reverse=True) # sort the pop by the reference of fitness sum_fits = sum(ind['fitness'] for ind in individuals) # sum up the fitness of the whole pop chosen = [] for i in range(k): u = random.random() * sum_fits # randomly produce a num in the range of [0, sum_fits], as threshold sum_ = 0 for ind in s_inds: sum_ += ind['fitness'] # sum up the fitness if sum_ >= u: chosen.append(ind) break chosen = sorted(chosen, key=itemgetter("fitness"), reverse=False) return chosen |
在这里我们对种群按照概率进行选择后代,适应度函数大的个体大概率被选择到下一代,最后我们对重新生成的新一代种群按照适应度从小到大进行排序,方便接下来的交叉操作。
crossoperate()方法
交叉是指将两个个体的基因片段在某一点或者某几点进行互换,常用的有单点交叉和双点交叉。它的过程如下:
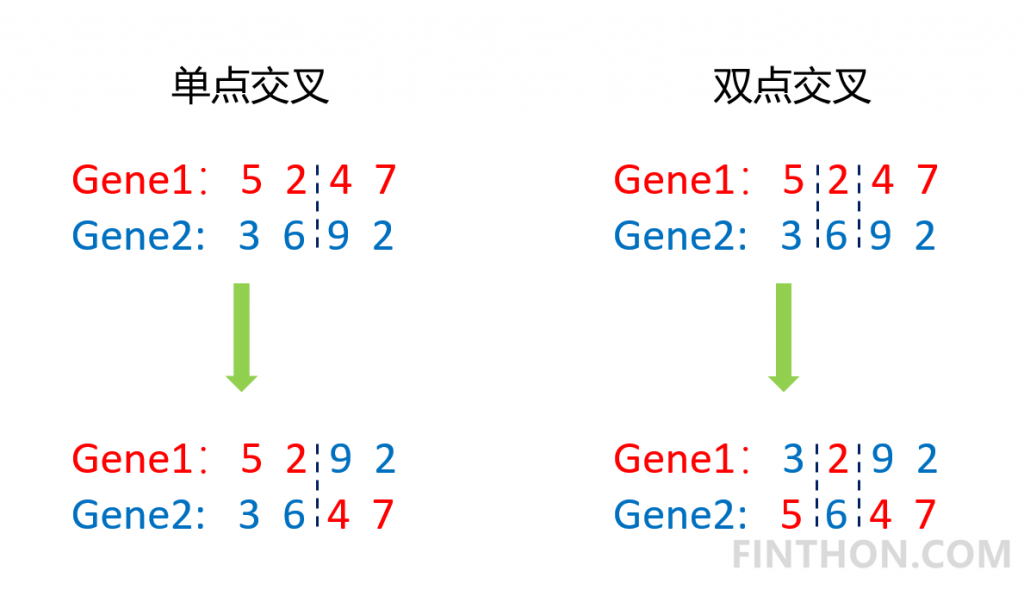
从图中可以看出,无论是单点交叉还是双点交叉都很大的改变了原来的基因序列,它是实现优化的重要手段。具体的实现代码如下:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | def crossoperate(self, offspring): dim = len(offspring[0]['Gene'].data) geninfo1 = offspring[0]['Gene'].data # Gene's data of first offspring chosen from the selected pop geninfo2 = offspring[1]['Gene'].data # Gene's data of second offspring chosen from the selected pop if dim == 1: pos1 = 1 pos2 = 1 else: pos1 = random.randrange(1, dim) # select a position in the range from 0 to dim-1, pos2 = random.randrange(1, dim) newoff1 = Gene(data=[]) # offspring1 produced by cross operation newoff2 = Gene(data=[]) # offspring2 produced by cross operation temp1 = [] temp2 = [] for i in range(dim): if min(pos1, pos2) <= i < max(pos1, pos2): temp2.append(geninfo2[i]) temp1.append(geninfo1[i]) else: temp2.append(geninfo1[i]) temp1.append(geninfo2[i]) newoff1.data = temp1 newoff2.data = temp2 return newoff1, newoff2 |
上面的代码实现了双点交叉,其中为了防止只有一个基因的存在,我们使用一个判断语句。
mutation()方法
变异在遗传过程中属于小概率事件,但是在种群数量较小的情况下,只通过交叉操作并不能产生优秀的后代,此时变异就显得非常重要了。通过适当的变异甚至能够产生更优秀的后代。变异的方式有很多种,常规的变异有基本位变异和逆转变异。它的过程如下:
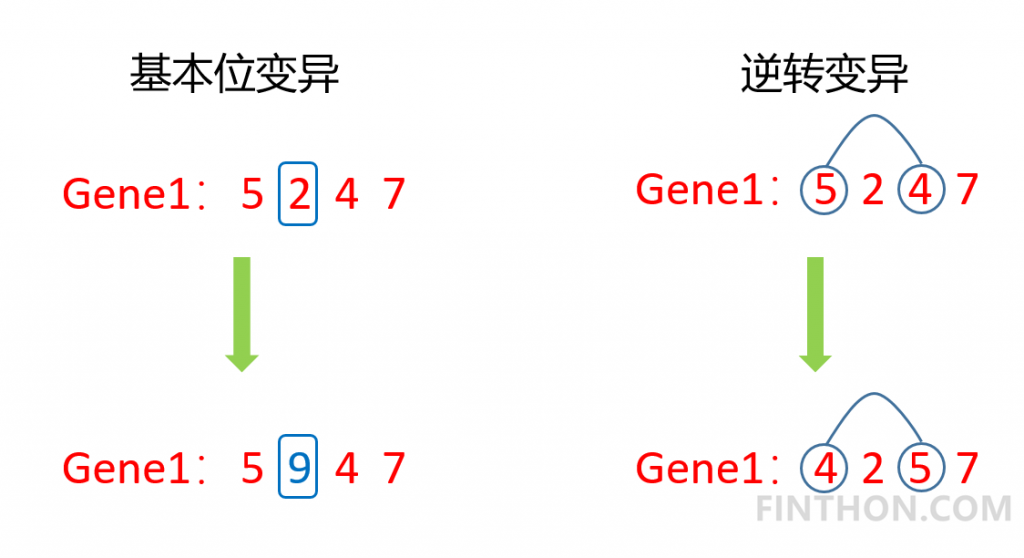
在这里我们实现单点变异:
| 1 2 3 4 5 6 7 8 9 10 | def mutation(self, crossoff, bound): dim = len(crossoff.data) if dim == 1: pos = 0 else: pos = random.randrange(0, dim) # chose a position in crossoff to perform mutation. crossoff.data[pos] = random.randint(bound[0][pos], bound[1][pos]) return crossoff |
同样为了防止只有一个基因的情况,使用判断语句。
GA_main()方法
遗传算法所有的轮子都写好后,我们接下来将它们整合到流程中。代码实现如下:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 | def GA_main(self): popsize = self.parameter[3] print("Start of evolution") # Begin the evolution for g in range(NGEN): print("############### Generation {} ###############".format(g)) # Apply selection based on their converted fitness selectpop = self.selection(self.pop, popsize) nextoff = [] while len(nextoff) != popsize: # Apply crossover and mutation on the offspring # Select two individuals offspring = [selectpop.pop() for _ in range(2)] if random.random() < CXPB: # cross two individuals with probability CXPB crossoff1, crossoff2 = self.crossoperate(offspring) if random.random() < MUTPB: # mutate an individual with probability MUTPB muteoff1 = self.mutation(crossoff1, self.bound) muteoff2 = self.mutation(crossoff2, self.bound) fit_muteoff1 = self.evaluate(muteoff1.data) # Evaluate the individuals fit_muteoff2 = self.evaluate(muteoff2.data) # Evaluate the individuals nextoff.append({'Gene': muteoff1, 'fitness': fit_muteoff1}) nextoff.append({'Gene': muteoff2, 'fitness': fit_muteoff2}) else: fit_crossoff1 = self.evaluate(crossoff1.data) # Evaluate the individuals fit_crossoff2 = self.evaluate(crossoff2.data) nextoff.append({'Gene': crossoff1, 'fitness': fit_crossoff1}) nextoff.append({'Gene': crossoff2, 'fitness': fit_crossoff2}) else: nextoff.extend(offspring) # The population is entirely replaced by the offspring self.pop = nextoff # Gather all the fitnesses in one list and print the stats fits = [ind['fitness'] for ind in self.pop] best_ind = self.selectBest(self.pop) if best_ind['fitness'] > self.bestindividual['fitness']: self.bestindividual = best_ind print("Best individual found is {}, {}".format(self.bestindividual['Gene'].data, self.bestindividual['fitness'])) print(" Max fitness of current pop: {}".format(max(fits))) print("------ End of (successful) evolution ------") |
在这个流程当中需要注意的是,经过selection()方法产生的新种群selectpop是按照适应度从小到大排列的,通过列表的pop()方法能够优先选择适应度大的两个个体进行后续的交叉操作;因为是pop()两次,所以种群的大小必须是偶数个。
完整代码如下:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 | import random from operator import itemgetter class Gene: """ This is a class to represent individual(Gene) in GA algorithom each object of this class have two attribute: data, size """ def __init__(self, **data): self.__dict__.update(data) self.size = len(data['data']) # length of gene class GA: """ This is a class of GA algorithm. """ def __init__(self, parameter): """ Initialize the pop of GA algorithom and evaluate the pop by computing its' fitness value. The data structure of pop is composed of several individuals which has the form like that: {'Gene':a object of class Gene, 'fitness': 1.02(for example)} Representation of Gene is a list: [b s0 u0 sita0 s1 u1 sita1 s2 u2 sita2] """ # parameter = [CXPB, MUTPB, NGEN, popsize, low, up] self.parameter = parameter low = self.parameter[4] up = self.parameter[5] self.bound = [] self.bound.append(low) self.bound.append(up) pop = [] for i in range(self.parameter[3]): geneinfo = [] for pos in range(len(low)): geneinfo.append(random.randint(self.bound[0][pos], self.bound[1][pos])) # initialise popluation fitness = self.evaluate(geneinfo) # evaluate each chromosome pop.append({'Gene': Gene(data=geneinfo), 'fitness': fitness}) # store the chromosome and its fitness self.pop = pop self.bestindividual = self.selectBest(self.pop) # store the best chromosome in the population def evaluate(self, geneinfo): """ fitness function """ x1 = geneinfo[0] x2 = geneinfo[1] x3 = geneinfo[2] x4 = geneinfo[3] y = x1**2 + x2**2 + x3**3 + x4**4 return y def selectBest(self, pop): """ select the best individual from pop """ s_inds = sorted(pop, key=itemgetter("fitness"), reverse=True) # from large to small, return a pop return s_inds[0] def selection(self, individuals, k): """ select some good individuals from pop, note that good individuals have greater probability to be choosen for example: a fitness list like that:[5, 4, 3, 2, 1], sum is 15, [-----|----|---|--|-] 012345|6789|101112|1314|15 we randomly choose a value in [0, 15], it belongs to first scale with greatest probability """ s_inds = sorted(individuals, key=itemgetter("fitness"), reverse=True) # sort the pop by the reference of fitness sum_fits = sum(ind['fitness'] for ind in individuals) # sum up the fitness of the whole pop chosen = [] for i in range(k): u = random.random() * sum_fits # randomly produce a num in the range of [0, sum_fits], as threshold sum_ = 0 for ind in s_inds: sum_ += ind['fitness'] # sum up the fitness if sum_ >= u: # when the sum of fitness is bigger than u, choose the one, which means u is in the range of # [sum(1,2,...,n-1),sum(1,2,...,n)] and is time to choose the one ,namely n-th individual in the pop chosen.append(ind) break # from small to large, due to list.pop() method get the last element chosen = sorted(chosen, key=itemgetter("fitness"), reverse=False) return chosen def crossoperate(self, offspring): """ cross operation here we use two points crossoperate for example: gene1: [5, 2, 4, 7], gene2: [3, 6, 9, 2], if pos1=1, pos2=2 5 | 2 | 4 7 3 | 6 | 9 2 = 3 | 2 | 9 2 5 | 6 | 4 7 """ dim = len(offspring[0]['Gene'].data) geninfo1 = offspring[0]['Gene'].data # Gene's data of first offspring chosen from the selected pop geninfo2 = offspring[1]['Gene'].data # Gene's data of second offspring chosen from the selected pop if dim == 1: pos1 = 1 pos2 = 1 else: pos1 = random.randrange(1, dim) # select a position in the range from 0 to dim-1, pos2 = random.randrange(1, dim) newoff1 = Gene(data=[]) # offspring1 produced by cross operation newoff2 = Gene(data=[]) # offspring2 produced by cross operation temp1 = [] temp2 = [] for i in range(dim): if min(pos1, pos2) <= i < max(pos1, pos2): temp2.append(geninfo2[i]) temp1.append(geninfo1[i]) else: temp2.append(geninfo1[i]) temp1.append(geninfo2[i]) newoff1.data = temp1 newoff2.data = temp2 return newoff1, newoff2 def mutation(self, crossoff, bound): """ mutation operation """ dim = len(crossoff.data) if dim == 1: pos = 0 else: pos = random.randrange(0, dim) # chose a position in crossoff to perform mutation. crossoff.data[pos] = random.randint(bound[0][pos], bound[1][pos]) return crossoff def GA_main(self): """ main frame work of GA """ popsize = self.parameter[3] print("Start of evolution") # Begin the evolution for g in range(NGEN): print("############### Generation {} ###############".format(g)) # Apply selection based on their converted fitness selectpop = self.selection(self.pop, popsize) nextoff = [] while len(nextoff) != popsize: # Apply crossover and mutation on the offspring # Select two individuals offspring = [selectpop.pop() for _ in range(2)] if random.random() < CXPB: # cross two individuals with probability CXPB crossoff1, crossoff2 = self.crossoperate(offspring) if random.random() < MUTPB: # mutate an individual with probability MUTPB muteoff1 = self.mutation(crossoff1, self.bound) muteoff2 = self.mutation(crossoff2, self.bound) fit_muteoff1 = self.evaluate(muteoff1.data) # Evaluate the individuals fit_muteoff2 = self.evaluate(muteoff2.data) # Evaluate the individua
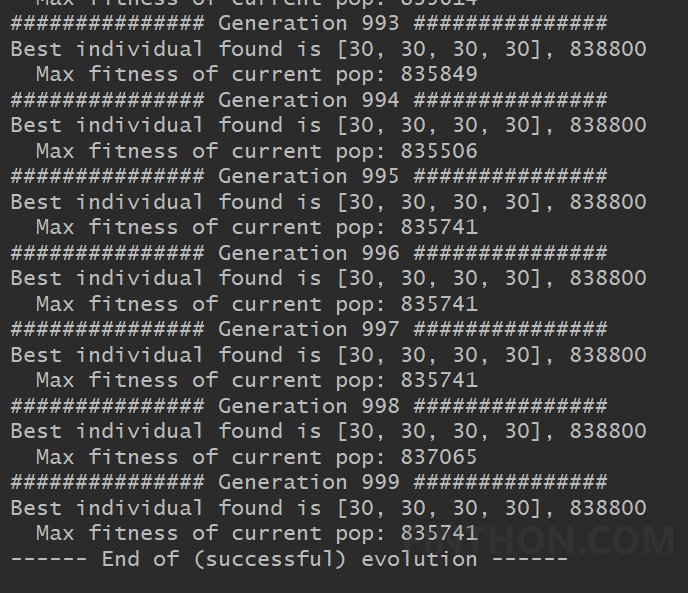
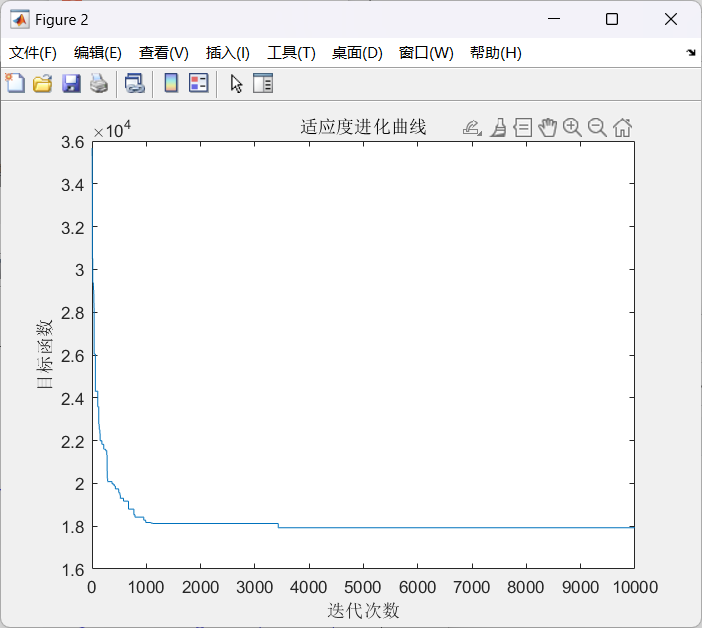
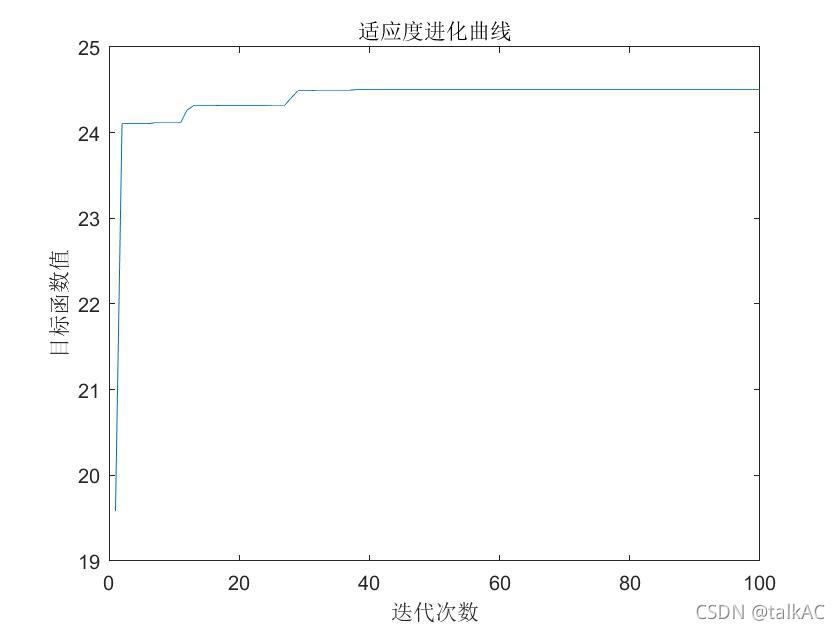
在 得到结果如下: 事实上按照目前的参数,在第342代的时候已经找到最优解。如果使用枚举法需要30*30*30*30=810000次才能寻找到最优解,通过遗传算法只计算了34200次,大大缩短最优解的搜索空间。 参考:Python手把手构建遗传算法(GA)实现最优化搜索 - FINTHON
|