1. 遗传算法简单介绍

1.1 理论基础

整个算法的基础就是达尔文的生物进化论，“物竞天择，适者生存” 这句话已经是常识了。

用雪兔做一个引子吧：

东北那旮瘩，有群原始雪兔，刚从未知物种进化而来，五颜六色（表现型）漂亮极了，称之为 I(0)。
（注意：种群初始化）

入夏了，雪兔们出来觅食，浅色兔在草地中无所遁形，被雪狐收割了一波（大批浅色+小批深色）。
入冬了，雪兔们出来觅食，深色兔在雪地中光彩夺目，被雪狐收割了一波（大批深色+小批浅色）。
（注意：自然选择过程）

春天到了，又到了兔兔们生孩的季节，雪兔们染色体内的基因进行 重组/不重组 ，产生一批受精卵。
（注意：交叉遗传过程）

受精卵内的生命活动非常强烈，造成了基因的 突变/不突变，产生了各种各样奇怪的小雪兔。
（注意：基因变异过程）

老雪兔们完成了自己繁衍的使命，全部不知所踪。留下新生代，继续在各种威胁下苟活，这一代叫 I(1)。

再次入冬入夏，雪兔们又出来觅食。。。。。。再次入冬，觅食。。。。。。入冬，觅食。。。。。。

就这样，50年后，基因突变和重组造就了种神奇的兔子：夏天褐色，冬天白色，可以轻易躲避雪狐的追捕

再次入冬入夏，雪兔们又出来觅食。。。。。。再次入冬，觅食。。。。。。入冬，觅食。。。。。。

这样，50年后，雪地里基本上见不到五颜六色的雪兔了，这时候雪兔们达到了兔生巅峰！

这就是遗传算法的理论基础，自然选择、交叉、变异、迭代，最终获得最优解。

注意：算法是根据表现型来进行选择，最终选出最优的表现型及其对应的基因。

1.2 算法要点

1.1 编码

编码是为了把我们的输入参数变成染色体（每个个体只有一条染色体），以便于进行交叉和遗传运算。

例如我们把雪兔的颜色进行划分， 0-255 （表现型）代表 黑->白 的不同程度，0就是纯黑的，255就是纯白的。

我们这里只谈一下简单的二进制编码，二进制编码中的每一个二进制位是一个基因，整个数字为染色体。

那么0-255共有256阶（表现型），我们可以用8位2进制数来表示（基因型）。

兔色为0的编码为 00000000，兔色为2的编码为 00000010，兔色为255的编码为 11111111。

1.2 适应度函数

适应度函数就是个体对环境的适应度，适应度越强的越能产生后代，保留自己的基因及表现型。

这里，我们假设灰色兔子的适应能力最强，即兔色为128的兔子不会被吃掉，设定函数为：

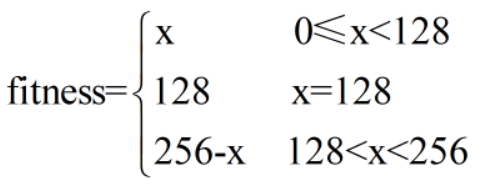
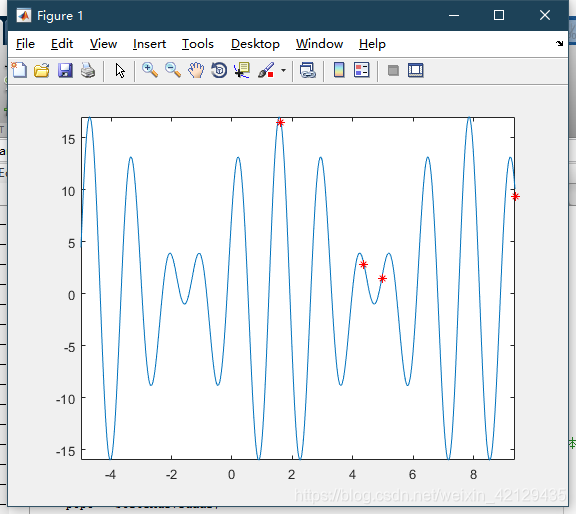
是一个最大值为128的分段函数，图像如下：

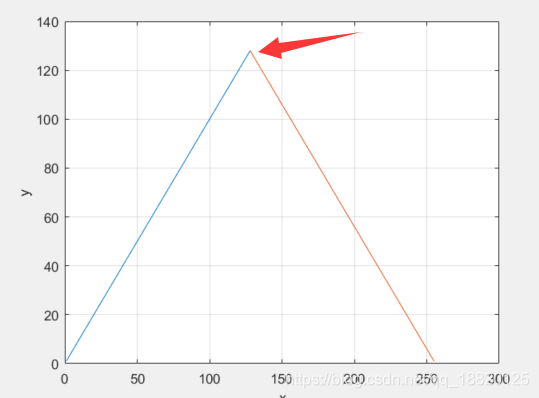
适应度函数的极值点一般是未知的，这里我们为了演示方便，就先展示出来。

1.3 基本流程

流程就和雪兔故事一样简单，如下所示：

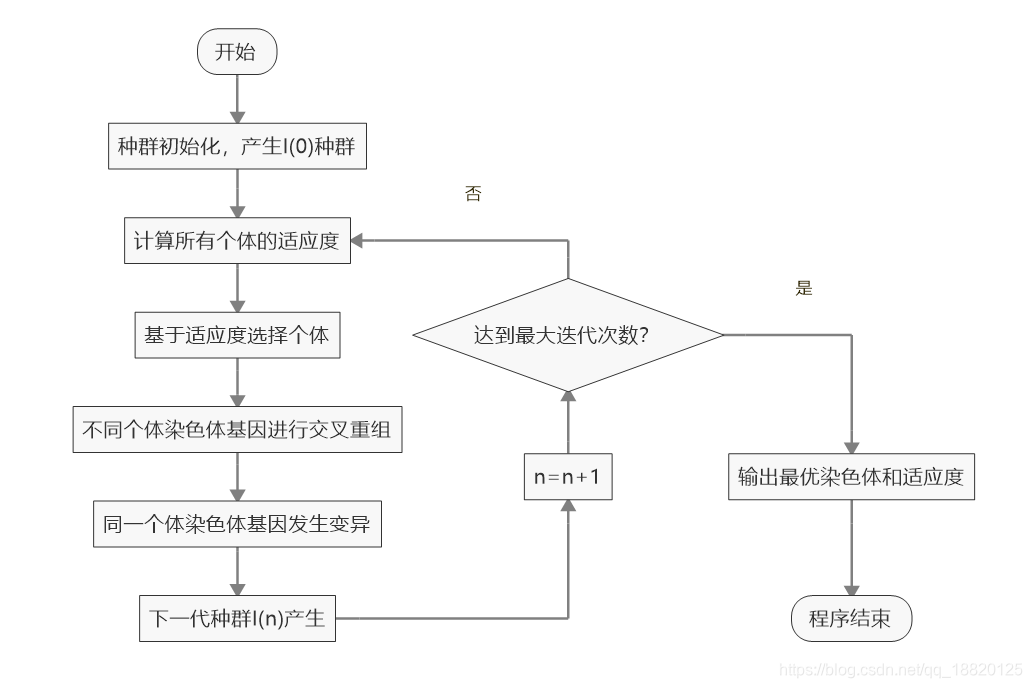
注意：迭代的终止条件可以不是最大迭代次数，比如规定为种群适应度值的方差小于某个值（即种群表现型趋于一致）。

2. 代码实例（MATLAB）

2.1 代码汇总

遗传算法代码（通用代码）：

function [bestChromosome,fitnessBest]=GA(numOfChromosome,numOfGene,iterationNum)
%% 函数功能：执行基于自适应遗传算法的卸载决策
%   输入：
%       numOfChromosome：染色体数量，即迭代的种群大小
%       numOfGene：基因的数量，即所用二进制编码的位数
%       iterationNum：迭代的总次数，达到迭代次数即终止迭代
%   输出：
%       bestChromosome：最优的染色体（即最优的输入）
%       fitnessBest：最优的适应度值（即最优的结果）%% 随机生成初始种群，种群大小为numOfChromosome，染色体中基因数为numOfGene
% lastPopulation：上一代的种群（染色体）
% newPopulation：新一代的种群（染色体）
% randi([0,1])会产生0或1的整数
lastPopulation=randi([0,1],numOfChromosome,numOfGene);
newPopulation=zeros(numOfChromosome,numOfGene);%% 进行遗传迭代，直至达到最大迭代次数iterationNum
for iteration=1:iterationNum%% 计算所有个体（染色体）的适应度，一共有numOfChromosome个适应度值fitnessAll=zeros(1,numOfChromosome);for i=1:numOfChromosomeindividual=lastPopulation(i,:);fitnessAll(i)=fitnessFunc(individual);end%% 如果达到最大迭代次数，跳出（不能再进行选择遗传和变异了）if iteration==iterationNumbreak;end%% 使用轮盘赌法选择numOfChromosome条染色体，种群中个体总数不变fitnessSum=sum(fitnessAll);fitnessProportion=fitnessAll/fitnessSum;% 使用随机数进行numOfChromosome次选择，保持种群中个体数量不变for i=1:numOfChromosomeprobability=rand(1);proportionSum=0;chromosomeIndex=1;for j=1:numOfChromosomeproportionSum=proportionSum+fitnessProportion(j);if proportionSum>=probabilitychromosomeIndex=j;break;endendnewPopulation(i,:)=lastPopulation(chromosomeIndex,:);end%% 将染色体进行配对，执行单点交叉lastPopulation=newPopulation;% 生成从1到numOfChromosome的无序排列，每两个相邻数字进行配对coupleAllIndex=randperm(numOfChromosome);for i=1:floor(numOfChromosome/2)coupleOneIndex=coupleAllIndex(2*i-1:2*i);% 定义两条染色体交叉的概率，自己选择probability=0.6;% 如果生成的随机数在交叉概率内，执行交叉操作if rand(i)<probability% 随机生成交叉的基因点，将两条基因进行交叉crossPosition=randi([1,numOfGene],1);newPopulation(coupleOneIndex(1),crossPosition:end)=lastPopulation(coupleOneIndex(2),crossPosition:end);newPopulation(coupleOneIndex(2),crossPosition:end)=lastPopulation(coupleOneIndex(1),crossPosition:end);endend%% 对每条染色体执行基本位变异操作lastPopulation=newPopulation;for i=1:numOfChromosome% 定义染色体变异的概率，自己选择probability=0.2;% 如果生成的随机数在变异概率内，执行变异操作if rand(1)<probability% 选择变异的位置mutatePosition=randi([1,numOfGene],1);% 将对应基因位置的二进制数反转if(lastPopulation(i,mutatePosition)==0)newPopulation(i,mutatePosition)=1;elsenewPopulation(i,mutatePosition)=0;endendend %% 完成了一次迭代，更新种群lastPopulation=newPopulation;
end%% 遗传迭代结束后，获得最优适应度值和对应的基因
fitnessBest=max(fitnessAll);
bestChromosome=newPopulation(find(fitnessAll==fitnessBest,1),:);

雪兔例子的适应度计算代码：

function fitness=fitnessFunc(chromosome)
%% 函数功能：计算染色体的表现型及其适应度
% 输入：
%       chromosome：染色体的基因序列
% 输出：
%       fitness：染色体（个体）的适应度值%% 计算雪兔染色体对应表现型
len=length(chromosome);
numList=2.^(len-1:-1:0);
x=sum(chromosome.*numList);%% 计算表现型对应的适应度
if x<128fitness=x;
elseif x>128fitness=256-x;elsefitness=128;end
end

2.1 初始化种群

%% 随机生成初始种群，种群大小为numOfChromosome，染色体中基因数为numOfGene
% lastPopulation：上一代的种群（染色体）
% newPopulation：新一代的种群（染色体）
% randi([0,1])会产生0或1的整数
lastPopulation=randi([0,1],numOfChromosome,numOfGene);
newPopulation=zeros(numOfChromosome,numOfGene);

这里使用随机数生成函数生成了numOfChromosome条染色体，每条染色体有numOfGene个基因。

将生成的种群放入lastPopulation中，每一行是一条染色体。

newPopulation相当于一个辅助数组，存储生成种群的中间结果。

2.2 计算适应度

    %% 计算所有个体（染色体）的适应度，一共有numOfChromosome个适应度值fitnessAll=zeros(1,numOfChromosome);for i=1:numOfChromosomeindividual=lastPopulation(i,:);fitnessAll(i)=fitnessFunc(individual);end

计算种群中所有个体的适应度，即把每一条染色体（个体）都放入适应度函数中，得到适应度结果。

2.3 迭代终止判断

    %% 如果达到最大迭代次数，跳出（不能再进行选择遗传和变异了）if iteration==iterationNumbreak;end

计算完适应度，如果达到终止条件，就不再进行选择、遗传和变异了。

否则你跳出循环时，种群适应度与计算的的适应度不匹配。

另一种方案：执行选择、遗传、变异，跳出循环后再次计算适应度即可。

2.4 自然选择（轮盘赌法）

    %% 使用轮盘赌法选择numOfChromosome条染色体，种群中个体总数不变fitnessSum=sum(fitnessAll);fitnessProportion=fitnessAll/fitnessSum;% 使用随机数进行numOfChromosome次选择，保持种群中个体数量不变for i=1:numOfChromosomeprobability=rand(1);proportionSum=0;chromosomeIndex=1;for j=1:numOfChromosomeproportionSum=proportionSum+fitnessProportion(j);if proportionSum>=probabilitychromosomeIndex=j;break;endendnewPopulation(i,:)=lastPopulation(chromosomeIndex,:);end

计算每个个体适应度占总适应度的比例，总适应度是一个饼图，每个个体占据一定的扇形区域。

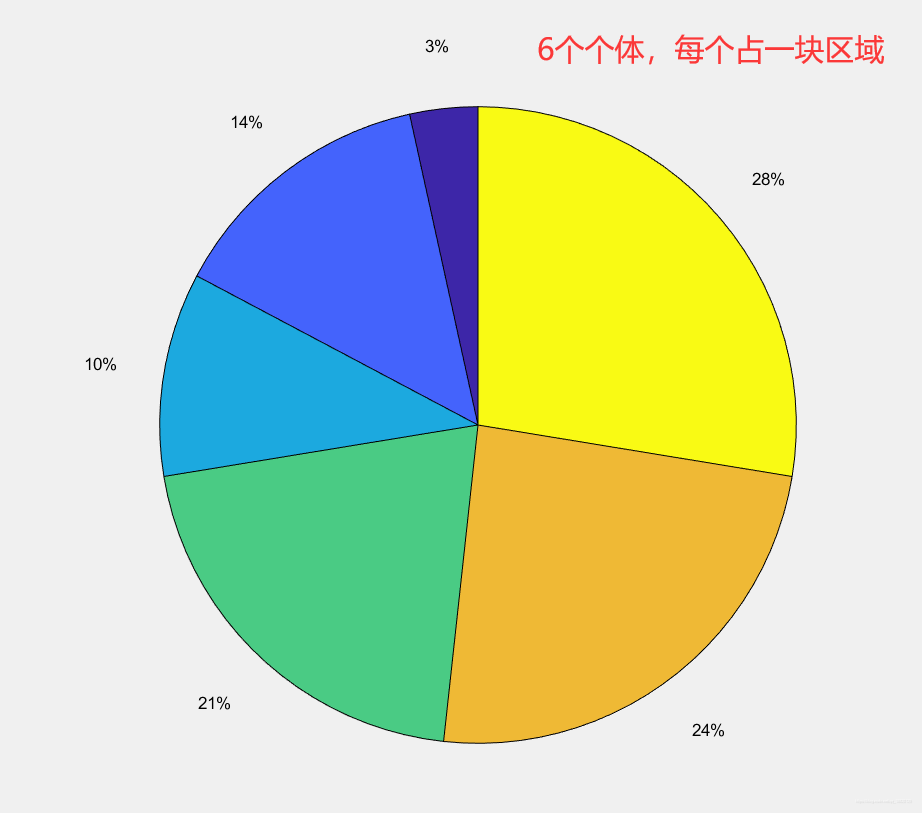
然后生成numOfChromosome个0-1的随机数，随机数落在哪个区域，哪个个体便被生存，可重复选择。

显然，适应度高的个体容易被选择，将自己的基因和表现型遗传下去。

2.5 配对交叉（单点）

    %% 将染色体进行配对，执行单点交叉lastPopulation=newPopulation;% 生成从1到numOfChromosome的无序排列，每两个相邻数字进行配对coupleAllIndex=randperm(numOfChromosome);for i=1:floor(numOfChromosome/2)coupleOneIndex=coupleAllIndex(2*i-1:2*i);% 定义两条染色体交叉的概率，自己选择probability=0.6;% 如果生成的随机数在交叉概率内，执行交叉操作if rand(i)<probability% 随机生成交叉的基因点，将两条基因进行交叉crossPosition=randi([1,numOfGene],1);newPopulation(coupleOneIndex(1),crossPosition:end)=lastPopulation(coupleOneIndex(2),crossPosition:end);newPopulation(coupleOneIndex(2),crossPosition:end)=lastPopulation(coupleOneIndex(1),crossPosition:end);endend

进行遗传的前提是配对，每两条染色体组合成一对，将两者的部分染色体进行交换。

单点交叉，顾名思义，选择染色体上的一个基因点，从这个基因点开始的两条染色体片段互换：

2.6 变异（基本位变异）

    %% 对每条染色体执行基本位变异操作lastPopulation=newPopulation;for i=1:numOfChromosome% 定义染色体变异的概率，自己选择probability=0.2;% 如果生成的随机数在变异概率内，执行变异操作if rand(1)<probability% 选择变异的位置mutatePosition=randi([1,numOfGene],1);% 将对应基因位置的二进制数反转if(lastPopulation(i,mutatePosition)==0)newPopulation(i,mutatePosition)=1;elsenewPopulation(i,mutatePosition)=0;endendend 

基本位变异就是选择一条染色体上的一个基因点，将其取反。

如染色体 11111111，选择其第四个基因进行基本位变异， 新染色体变为 11101111

2.7 获得最优解

%% 遗传迭代结束后，获得最优适应度值和对应的基因
fitnessBest=max(fitnessAll);
bestChromosome=newPopulation(find(fitnessAll==fitnessBest,1),:);

迭代结束之后，我们求出最大的适应度及其对应的染色体（个体），这就是我们需要的最优个体。

2.8 雪兔遗传结果

我们运行2.1给出的GA函数，在命令行输入以下代码运行：

[bestChromosome,fitnessBest]=GA(40,8,60)

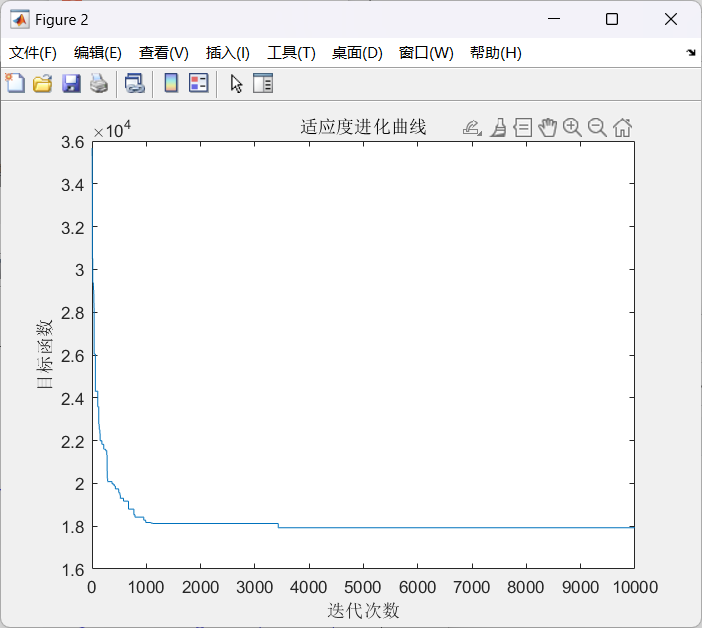
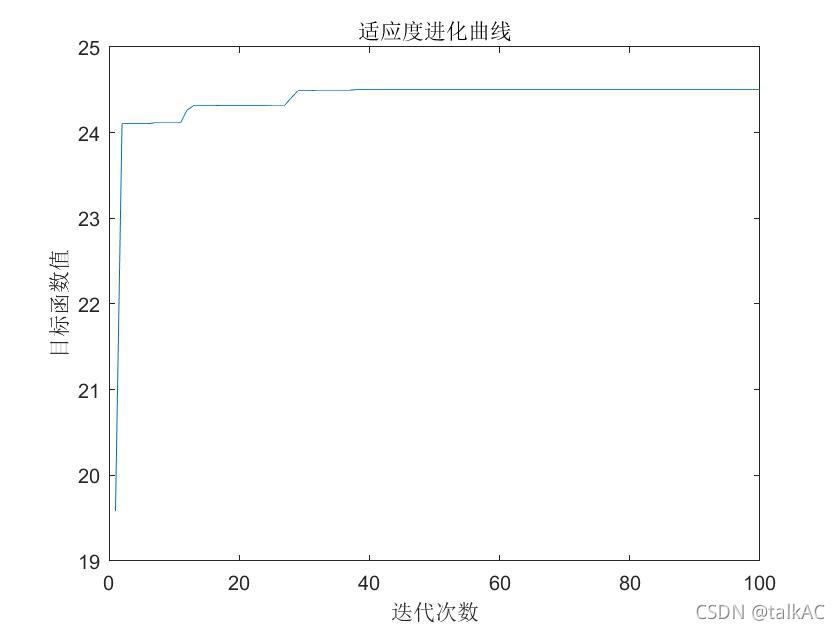
40个染色体进行60次迭代。多次这行代码，发现结果可以不同，如下：

虽然结果不尽相同，但都接近最优解128，这是遗传算法本身的局限，不一定能获得最优解。

2.9 改善遗传算法的方法

通过2.8我们知道，遗传算法有时候只能逼近最优解，那么有什么方法能让他达到更好的逼近效果呢？

这里有几个方案：

1. 使用自适应遗传和变异概率
2. 增加种群中个体数量
3. 增大迭代次数
4. 使用双点交叉法
5. 采用多样的变异方法
6. 更改编码方式（某些情况）
7. 更换适应度函数，将个体适应度的差距拉大
8. 更换选择方法，轮盘赌法是最基本的方法，不科学

大家可以自行了解，以后可能会继续就这几个方面探讨。

3. 多多交流！