算法理解-遗传算法（Genetic Algorithm）（一个带计算过程的例子）

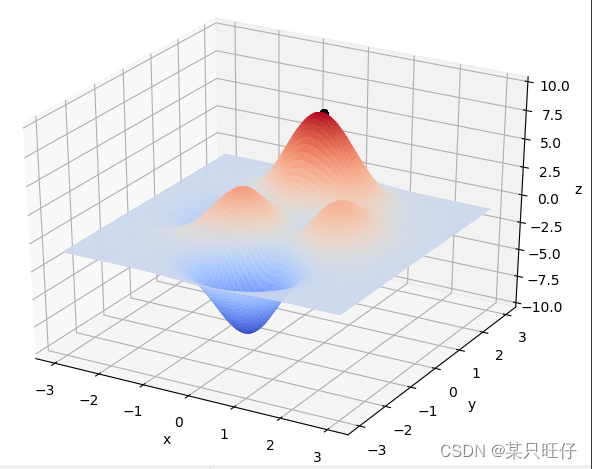
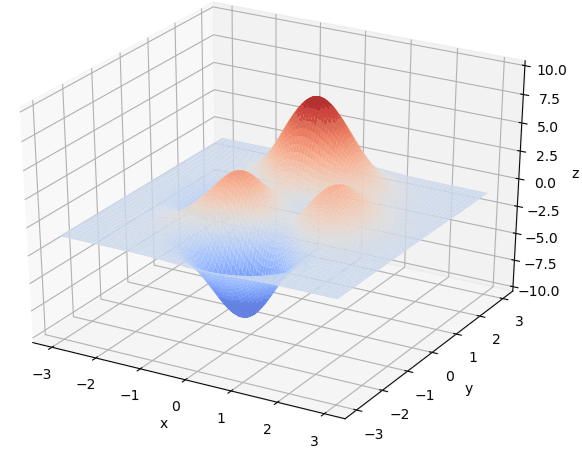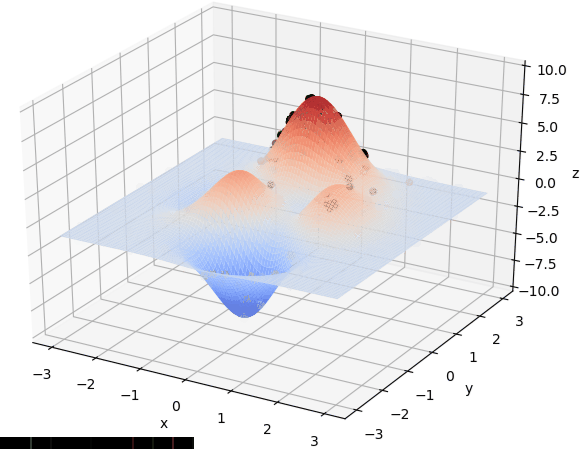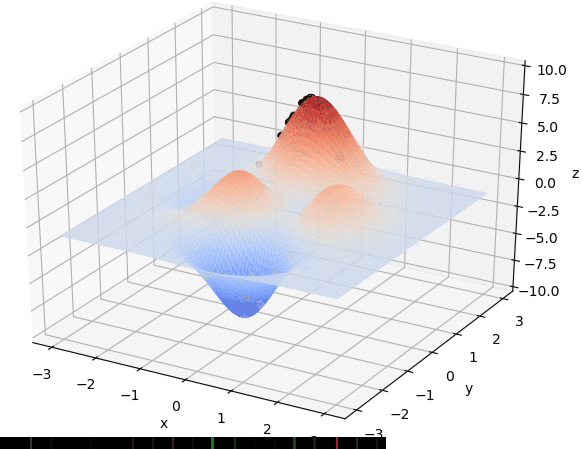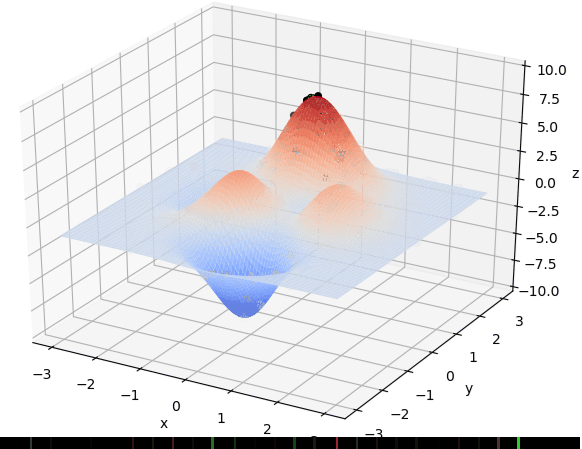
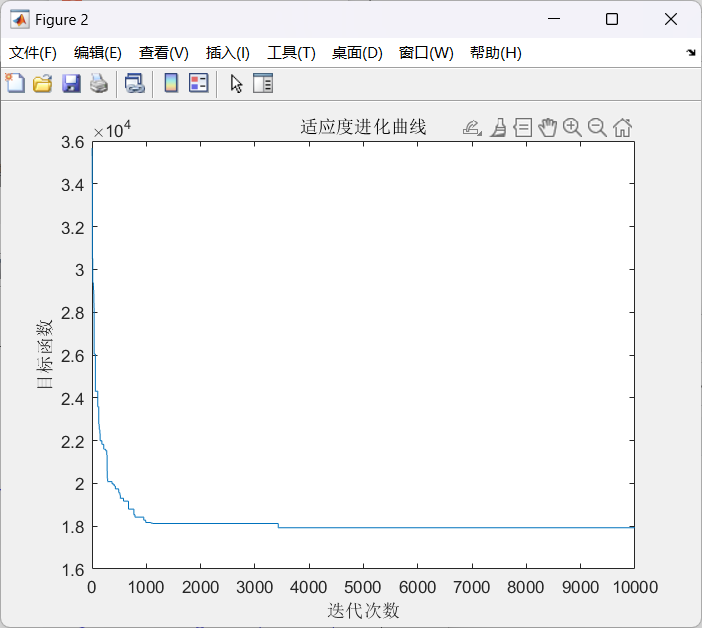
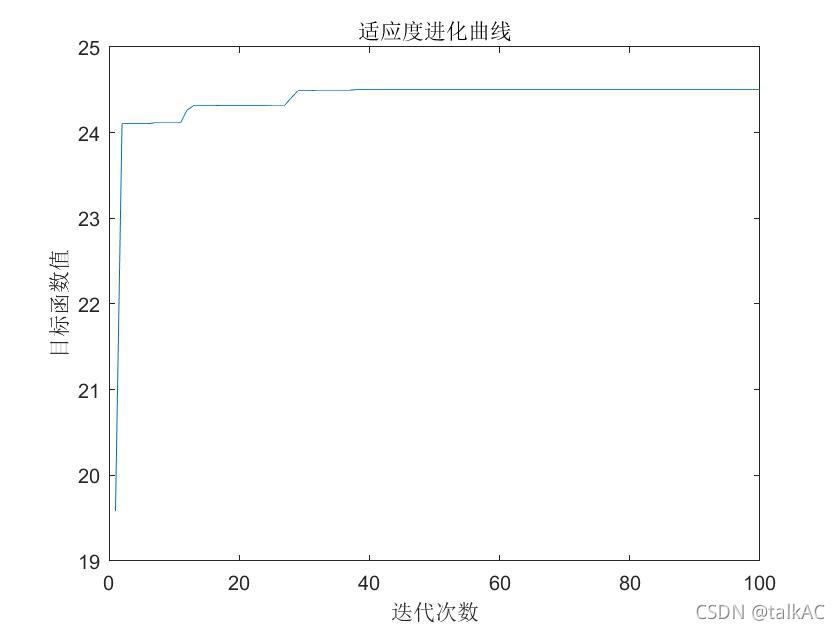
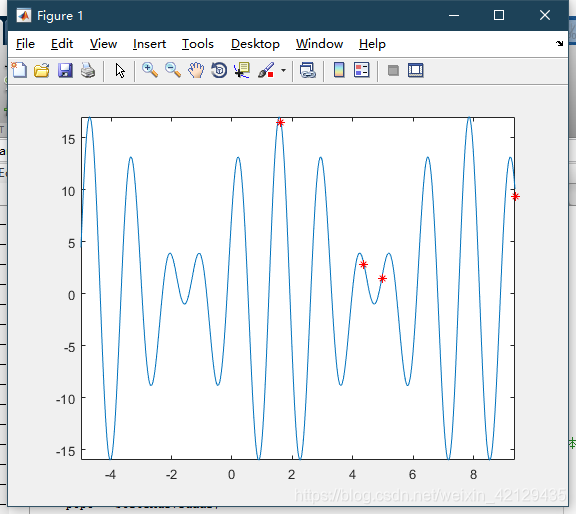
想要快速的了解一个算法，最好的方式便是拿个例子手动进行实现算一遍。这里借鉴了网络上的一个例子，求解如下的一个函数：

f (x) = x * s i n (10 * π * x) + 2 x \in [- 1, 2]

$f(x) = x*sin(10*\pi*x)+2 \\ x \in[-1, 2]$
其函数图像为：
suitFun

例子来源：
http://blog.csdn.net/emiyasstar__/article/details/6938608/

求解流程与概念

染色体（编码）

在遗传算法中，一个个体一般只包含一条染色体。染色体上包含这一组基因组。

基因 ( Gene ) ：一个遗传因子。
染色体 ( Chromosome ) ：一组的基因。
个体 ( individual )：单个生物。
群体：一群个体

在上述的例子中自变量只有x，所有只有一个gene，因此在本例子中：

一 个 个 体 = 一 条 染 色 体 = 一 个 基 因

$一个个体 = 一条染色体 = 一个基因$
将x表达为gene的过程，称之为编码，常见的编码格式有二进制编码和浮点编码。本文采用2进制编码：

设我们求解精度为 $e =0.01$ ，
那么我们需要将x的区间【-1，2】，切分成 $(2- - 1)/0.01 = 300$ 份。
又因为采用二进制编码所以实际需要的编码位数为： $2^8=256 < 300 < 2^9=512$ 故当我们需要精度为0.01时，采用二进制编码最少需要9位数。
那么实际的求解精度为：
$e = 3 512 \approx 0.00586$ $e= \frac{3}{512} \approx 0.00586$

有编码就存在着解码，按照本文的例子，可以想到以下的映射：

000000000 = - 1 111111111 = 2

$000000000 = -1 \\ 111111111 = 2$
因此可以得到以下的解码公式：

(111111111) i n t o 10 * e - 1 = 512 * 3 512 - 1 = 2 (000000000) i n t o 10 * e - 1 = 0 - 1 = - 1

$(111111111)_{into10}*e - 1 = 512*\frac{3}{512}-1 = 2\\ (000000000)_{into10}*e - 1 = 0 - 1 = -1$
ps:忽略上述由二进制转换为十进制的写法细节，不知道怎么写其数学表达式。
其中编码和解码的R代码

GetCodeParameter <- function(e, limitX){# 获取编码的缩放比例，用于解码或者编码（二进制）# Args ： e:求解精度#        limitX:X的范围# return: bitsPower:二进制编码位数#         e:真实求解精度#         diff:解码公式的中的常数range <- limitX[2] - limitX[1] # 区间长度splitNum <- range/e            # 需要切割位数bitsPower <- 1 while(2^bitsPower <= splitNum ){bitsPower <- bitsPower + 1}xMax <- max(limitX)e <- range/2^bitsPower        # 精度大小diff <- 2^bitsPower*e - xMax  # 缩放差值 1 c(bitsPower, e, diff)         # 返还结果 
}DeCode <- function(x, limitX, codeParameter){# 解码# Args: x:需要解码的个体#       limitX: x的取值范围#       codeParameter：包含bitsPower、e、diff# return:x：解码后的xx <- strtoi(x, base = 2) # 转换为10进制x <- x*codeParameter[2]-codeParameter[3]x
}

适者生存

适者生存 ( The survival of the fittest )：对环境适应度高的个体参与繁殖的机会比较多，后代就会越来越多。适应度低的个体参与繁殖的机会比较少，后代就会越来越少。
适应度指的是求解的目标，该例子中适应度计算公式便是求解的目标：

f (x) = x * s i n (10 * π * x) + 2

$f(x) = x*sin(10*\pi*x)+2$
其中

f(x) $f(x)$ 便是适应度计算公式。
适者生存其实指的是对后代的一种选择策略，常见的选择策略有轮盘赌、锦标赛、精英保留策略。轮盘赌就是按照一定的概率抽取子代，重复n次，每个个体被抽中的概率为：

p i = f ( x i ) \sum n j = 1 f ( x j )

$p_i = \frac{f(x_i)}{\sum^n_{j=1}f(x_j)}$
轮盘赌举例说明：

# 有这么一个由10个个体组成的群体
group <- CreateGroup(groupNum, codeParameter)
group
# "101100100" "010001100" "000010010" "010010011" "000011101" 
# "011001111" "000001100" "000011010" "111100000" "000001011"# 计算每人的适应度
adaptive <- myFun(group)  # myFun = x*sin(10pi*x)+2
# 2.464  1.893  2.153  1.870  2.673 
# 2.084  1.253  2.845  2.694  1.159  # 每人的生存概率
existProb <- adaptive/sum(adaptive)
# 0.117 0.090 0.102 0.089 0.127 
# 0.099 0.059 0.135 0.128 0.055# 按照生存概率生成下一代，即重复放回抽取N次。
group <- sample(group, groupNum,prob = existProb, replace = T)
group # 新的群体
# "000001100" "000010010" "101100100" "010010011" "010001100" 
# "000011010" "000010010" "011001111" "000011010" "000001011"# 产生的下一代中有一些人被淘汰了
length(unique(group))
8

锦标赛进行优胜劣汰的方法是：每次从群体中随机抽取p个人，将p个人中适应度最好的保留下来，重复N次，得到N个保留下的个体形成下一代。

交叉

交叉指的是交换染色体片段产生后代两个新的后代，例如典型的单点交叉方式：随机选择两个个体进行交叉，按照以下的方式产生新的子代。
基因交换
配上代码

candidate  <- 1:groupNum       # 可以进行配对的下标
parentNum <- floor(groupNum/2) # 父母对，这里10个群体有5对# 随机配成5对
parentInx1 <- sample(candidate, parentNum, replace = F)                              
parentInx2 <- sample(candidate[!candidate %in% parentInx1], parentNum, replace = F) 
parentInx1  
# 3   5  8  9  6
parentInx2
# 10  4  1  7  2# 这里便形成了5对， 3与10配对， 5与4配对···
# 以其中一对举例，"101100100" "000001011"
# 随机产生交换点，codeParameter[1] = 9为编码的长度
matingPoint <- sample(2:(codeParameter[1]-1), 1, replace = T) 
matingPoint
# 6
previousGene_1 <- substr(parent1, 1, matingPoint[i2]) # 提取前半段
lastGene_1 <- substr(parent1, matingPoint[i2]+1, codeParameter[1]) # 提取后半段
previousGene_2 <- substr(parent2, 1, matingPoint[i2])
lastGene_2 <- substr(parent2, matingPoint[i2]+1, codeParameter[1])
# 交叉，产生后代
child_1 <- paste(previousGene_1, lastGene_2, sep="")
child_2 <- paste(previousGene_2, lastGene_1, sep="")
child_1；child_2 
#"101100011" "000001100"

交叉操作存在着多种方式，例如：多点杂交、均匀杂交，离散杂交、中间杂交、线性杂交和扩展线性杂交等算法。其中有些交叉操作是基于编码的方式的。

变异

变异的作用，指的是染色体的某个基因片段或者某个基因点发生突变。例如单点突变可以通过下图进行表示：
这里写图片描述
突变的作用，是希望能够摆脱局部最优点，往更好的地方去。但是效果具有很大的随机性。

mutationProb <- 0.01 # 变异概率
# 按照突变概率生成10个0和1，1表示发生突变，0表示没有发生突变
mutationGene <- sample(c(0,1), groupNum, replace = T,prob = c(1-mutationProb, mutationProb))
mutationGene
# 0 0 0 0 0 1 0 0 0 0# 变异位置下标
mutationIdx <- which(mutationGene==1)
lenMutation <- length(mutationIdx)
if (lenMutation> 0) { # 当存在变异的基因时# 根据变异个数，随机k个产生变异位置matingPoint <- sample(1:codeParameter[1], lenMutation, replace = T) for (i in 1:lenMutation){# 变异group[mutationIdx[i]] <- Mutation(group[mutationIdx[i]], matingPoint[i]) }}

总流程

遗传算法的求解过程，是一个不断重复的过程，其流程如图所示：
流程图

求解结果

贴图比较好展示：

这里附上一个小知识：
假如在R中想要将其过程以一个动态过程展示出来，可以通过animation包进行实现。其中HTML格式输出的话，还能进行交互式的调整展示的速度。
其过程也很简单，每次迭代时，都将图画扔进一个list当中然后print出来。例如：

library(animation)
saveHTML({for(i in 1:93){print(plotGA[[i]])}
})

效果如下：
这里写图片描述

代码汇总

#1. 初始化
#--- 目标函数
myFun <- function(x){   # 求解函数 亦 适应度函数x*sin(10*pi * x) + 2
}
#--- 求解参数
limitX <- c(-1, 2)   # 【-1，2】之间取值
e <- 0.01            # 小数点后2位 
groupNum <- 50       # 产生的群体数
mutationProb <- 0.01 # 变异概率
generation <- 500    # 迭代数目
plotGA <- list()     # 存储图片，画连续图用#2. 编码
#--- 获取编码参数
codeParameter <- GetCodeParameter(e, limitX)
#--- 产生群体
group <- CreateGroup(groupNum, codeParameter)#3. 种群繁衍过程
for(i in 1:generation){#3.1 计算适应度deCodeGroup <-  DeCode(group, limitX, codeParameter) adaptive <- myFun(deCodeGroup)          #3.2 适者生存existProb <- adaptive/sum(adaptive)# 计算生存概率group <- sample(group, groupNum,prob = existProb, replace = T) # 生存的个体#--- plotmeanAdaptive <- mean(adaptive)maxAdaptive <- max(adaptive)main <- paste("generation", i)plotGA[[i]] <- plotShow(x = deCodeGroup, y = adaptive, limitX, main, meanAdaptive, maxAdaptive)#3.3 杂交（两两配对）#--- 选择配对对象candidate  <- 1:groupNumparentNum <- floor(groupNum/2)parentInx1 <- sample(candidate, parentNum, replace = F)                              #parentInx2 <- sample(candidate[!candidate %in% parentInx1], parentNum, replace = F)  ##--- 选择配对点matingPoint <- sample(2:(codeParameter[1]-1), parentNum, replace = T)#--- 配对newgroup <- NULLfor(i2 in 1:parentNum){previousGene_1 <- substr(group[parentInx1[i2]], 1, matingPoint[i2])lastGene_1 <- substr(group[parentInx1[i2]], matingPoint[i2]+1, codeParameter[1])previousGene_2 <- substr(group[parentInx2[i2]], 1, matingPoint[i2])lastGene_2 <- substr(group[parentInx2[i2]], matingPoint[i2]+1,codeParameter[1])child_1 <- paste(previousGene_1, lastGene_2, sep="")child_2 <- paste(previousGene_2, lastGene_1, sep="")newgroup <- c(newgroup, child_1, child_2)}single <- which(!candidate %in% c(parentInx1, parentInx2))  # 将单身狗添加回去group <- c(newgroup, group[single])#3.4 变异#--- 选择变异基因mutationGene <- sample(c(0,1), groupNum, prob = c(1-mutationProb, mutationProb), replace = T)#--- 变异位置点mutationIdx <- which(mutationGene==1)#--- 变异(0 -> 1; 1 -> 0)lenMutation <- length(mutationIdx)if( lenMutation> 0){matingPoint <- sample(1:codeParameter[1], lenMutation, replace = F)for (i in 1:lenMutation){group[mutationIdx[i]] <- Mutation(group[mutationIdx[i]], matingPoint[i])}}#3.5 结束条件if((maxAdaptive - meanAdaptive) <= e) break()
}