目录
前言
适应度函数和目标函数的关系
1. 常规遗传算法
2.结合非线性规划fmincon函数的遗传算法
2.1 fmincon非线性规划函数使用
2.2 结合非线性规划fmincon函数的遗传算法使用及示例
2.2.1 编码
2.2.2 选择
2.2.3交叉
2.2.4变异
2.2.5非线性规划fmincon函数
2.2.6主程序
2.2.6 运行结果
3.封装函数ga和gamultiobj的遗传算法
3.1使用ga函数求最小值最大值
3.1.2例子①求最小值
3.1.2例子②求最小值
3.1.3例子②求最大值
3.2使用gamultiobj函数求极值问题
4.optimtool工具箱的遗传算法实例介绍
5. 学习问题
前言
对于遗传算法的基本操作无非就是,初始化种群,选择/复制、交叉、变异等几个关键的迭代寻找最优解步骤,群体中的每个个体代表问题的一个解,然后针对早熟/陷入局部最优,又提出各种改进的遗传算法,以及多目标优化的遗传算法等延伸。对于基础的理论部分,读者可以自行补充。由于我自己也是刚开始接触学习,这里做一些小总结,主要是采用m语言编写初始化、选择、交叉、变异步骤的常规遗传算法、结合非线性规划fmincon函数的遗传算法、使用封装函数ga和gamultiobj的遗传算法,以及使用optimtool工具箱的遗传算法实例介绍,有兴趣的读者可以作为参考,谢谢!
适应度函数和目标函数的关系
这里我想声明一下自己学习中卡住的一个地方,就是适应度函数和目标函数的关系。目标函数指的是我们需要最大化或者最小化的目标,当求目标函数的最大值时,适应度函数常取为目标函数,这样适应度值越大的个体,函数值越大,个体最优;当求目标函数的最小值时,适应度函数常取为目标函数的导数或者相反数,这样适应度值越大的个体,函数值越小,个体最优。
1. 常规遗传算法
这里为了方便大家学习,选用的是b站up主讲解的一个视频,很简单的寻找sinx最大/最小值的一个当目标优化例子,但是up主手把手教你写,保证能上手,链接:
遗传算法之函数 matlab手敲代码 看一次绝对印象深刻!_哔哩哔哩_bilibili
这里附上代码和注释
目标函数:
function y = func1(x)y=sin(x);
end主函数:
%b站视频链接https://www.bilibili.com/video/BV1s34y177Xo/?spm_id_from=333.999.0.0&vd_source=4111f25c8210633781435d0034f8971b
clear;%清屏
clear all;%清空变量
close all;%清空窗口
NP=100;%种群数量
L=40;%每个个体基因总数
Pc=0.8;%交叉率
Vc=0.2;%变异率
N=1000;%迭代次数
parent=randi([0,1],NP,L);%真正的初始化,真值
child=randi([0,1],NP,L);
x=randi([0,1],1,L);
fit=randi([0,1],1,L);
fitvalue=randi([0,1],1,L);
Xx=0;%下限
Xs=10;%上限
trace=randi([0,1],1,NP);
for k=1:N%将parent的二进制数转化成十进制for i=1:NPcount=0;%处理每一行for j=1:Lcount=count+2^(j-1)*parent(i,j);end%复制x和fitx(i)=count*(Xs-Xx)/(2^L-1);fit(i)=func1(x(i));end%对fit进行一些简单处理maxfit=max(fit);minfit=min(fit);rr=find(fit==minfit);%一维数组(因为可能有多个最小值,所以有多个下标),找最小适应度值pbest=parent(rr(1,1),:);%用于等下给下一个父代赋值fitvalue=(fit-min(fit))/(max(fit)-min(fit));%归一化操作fitvalue=fitvalue./sum(fitvalue);%每个元素加起来等于1fitvalue=cumsum(fitvalue);%累加和,使元素从0到1逐渐增大,最后一个元素为1%用轮盘赌选择i=1;j=1;ms=rand(1,NP);while i<=NPif ms(i)<=fitvalue(j)child(i,:)=parent(j,:);i=i+1;elsej=j+1;endend%交叉for i=1:2:NPr=rand;if r<Pcq=randi([0,1],1,L);for j=1:Lif q(j)==1 %如果产生的随机基因==1,将相邻个体相同位置的基因进行对换%交换temp=child(i,j);child(i,j)=child(i+1,j);child(i+1,j)=temp;endendendend%变异for i=1:round(NP*Vc) %行迭代次数p=randi([1,NP],1,1);%行号for j=1:round(L*Vc) %列迭代次数q=randi([1,L],1,1);%列号child(p,q)=~child(p,q);%将基因去反变异endend%筛选(下一代)parent=child;parent(1,:)=pbest;trace(k)=minfit;disp(['第',num2str(k),'次迭代']);
end
%输出图形
plot(trace);
xlabel('迭代次数');
ylabel('适应值');
title('遗传算法');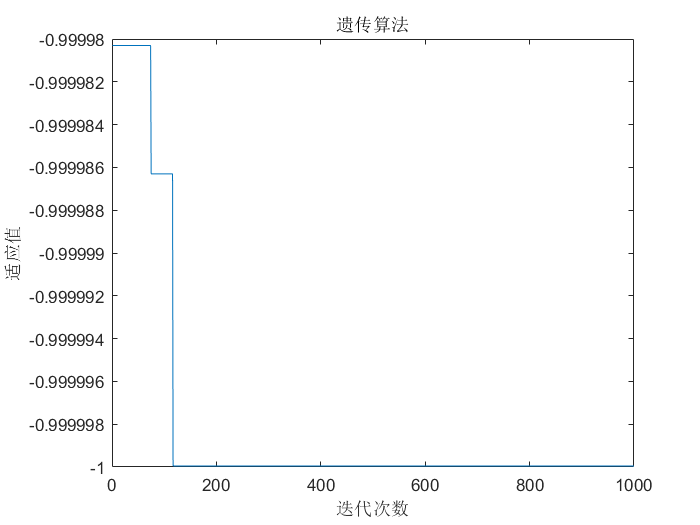
注:这里展示的是寻找最小值。
对于网上有很多代码,其实是类似的,还有的是将选择、交叉、变异等进行分文件编写,或者将初始换种群中的编码等进行分文件编写,所以算法上是相同的,根据个人习惯而定。
2.结合非线性规划fmincon函数的遗传算法
2.1 fmincon非线性规划函数使用
由于matlab的求极值的函数库都是默认最小值,如果求最大值取反即可,所以fmincon函数也是一样的。
首先介绍一下什么叫非线性规划,它的基本框架是:
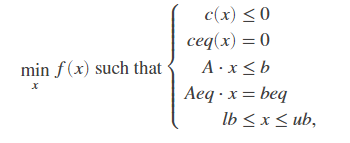
为了方便让大家上手使用和理解参数的含义,这里再给出fmincon函数的格式:
[x,xfval] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
输出:
x表求解完成后的变量值大小
x表求解完成后的目标函数值大小
输入:
fun:对应非线性函数框架中的目标函数f(x),如果使用分文件编写,直接写文件名,如果不分文件以匿名函数编写,则以匿名函数方式呈现:@fun
x0:目标函数自变量x的初值
A:线性不等式约束的左侧系数矩阵,默认为[]
b:线性不等式约束右侧系数,默认为[]
Aeq:线性等式约束的左侧系数矩阵,默认为[]
beq:线性等式约束右侧系数,默认为[]
nonlcon:代表非线性的约束条件,这个一般需要分文件编写,格式为:
function [c,ceq] = nonlcon(x),其中c表示非线性不等式约束,ceq表示非线性等式约束
lb、ub:目标函数自变量x的取值范围,即上下限
options:设定遗传算法运行时的参数,如交叉、变异的概率、种群大小、迭代次数和停止条件等。主要是使用gaoptimset函数(老版)或optimoptions函数(新版)进行设定,gaoptimset函数和optimoptions函数的格式为:
options = gaoptimset('param1',value1,'param2',value2,...)
options = optimoptions(SolverName,Name,Value)
如:options=gaoptimset('PopulationSize',100),表示初始种群的大小为100。
是不是很简单,相信大家已经理解和学会如何去使用fmincon函数了,这里给出一个综合的实例进行学习:
![]()
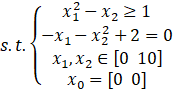
非线性约束(分文件):
function [c,ceq] = mynonlcon(x)
c = x(1)^2-x(2)-1;%非线性不等式约束
ceq = -x(1)-x(2)^2+2;%非线性等式约束主文件(运行文件):
x0 = [0 0];
A = [];b = [];%线性不等式约束,因为没有可以省略默认为[]
Aeq = [];beq = [];%线性等式约束,因为没有可以省略默认为[]
lb = [0 0];ub = [10 10];
nonlcon = @mynonlcon;
fun = @(x)x(1)^2+x(2)^2+8;
[x,xfval] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)求解结果:
x =
0.5000 1.2247
xfval =
9.7500
2.2 结合非线性规划fmincon函数的遗传算法使用及示例
算法结合的思想:

例子:

2.2.1 编码
常用的编码方式为二进制编码和十进制/实数编码,十进制编码的优势在于不用解码/数值转换并且求解精度高。这里采用十进制编码:
function ret=Code(lenchrom,bound)
%本函数将变量编码成染色体,用于随机初始化一个种群
% lenchrom input : 染色体长度
% bound input : 变量的取值范围
% ret output: 染色体的编码值flag=0;
while flag==0pick=rand(1,length(lenchrom));ret=bound(:,1)'+(bound(:,2)-bound(:,1))'.*pick;%线性插值,即将随机产生的基因转换到变量范围内flag=test(lenchrom,bound,ret); %检验染色体的编码值可行性,判断是否在都转换到变量区间
end验证是否初始化种群编码的数值是否均在变量范围内[0 0.9*pi],具体其他作用还没看懂,没有会运行很慢。
function flag=test(lenchrom,bound,code)
% lenchrom input : 染色体长度
% bound input : 变量的取值范围
% code output: 染色体的编码值flag=1;
[n,m]=size(code);for i=1:nif code(i)<bound(i,1) || code(i)>bound(i,2)flag=0;end
end2.2.2 选择
选择机制有许多种,最流行的属轮盘赌选择法,也叫适应度比例法或蒙特卡罗选择法,其特点是个体被选中的概率与其在群体环境中的相对适应度成正比。这里采用轮盘赌
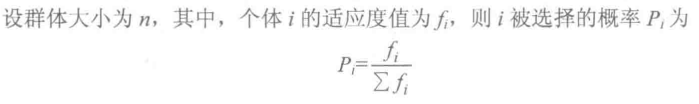
function ret=Select(individuals,sizepop)
% 本函数对每一代种群中的染色体进行选择,以进行后面的交叉和变异
% individuals input : 种群信息
% sizepop input : 种群规模
% opts input : 选择方法的选择
% ret output : 经过选择后的种群individuals.fitness= 1./(individuals.fitness);%选择目标函数的函数的倒数为适应度
sumfitness=sum(individuals.fitness);
sumf=individuals.fitness./sumfitness;
index=[];
for i=1:sizepop %转sizepop次轮盘pick=rand;while pick==0pick=rand;endfor j=1:sizepoppick=pick-sumf(j);if pick<0index=[index j];break; %寻找落入的区间,此次转轮盘选中了染色体i,注意:在转sizepop次轮盘的过程中,有可能会重复选择某些染色体endend
end
individuals.chrom=individuals.chrom(index,:);
individuals.fitness=individuals.fitness(index);
ret=individuals;2.2.3交叉
function ret=Cross(pcross,lenchrom,chrom,sizepop,bound)
%本函数完成交叉操作
% pcorss input : 交叉概率
% lenchrom input : 染色体的长度
% chrom input : 染色体群
% sizepop input : 种群规模
% ret output : 交叉后的染色体for i=1:sizepop % 随机选择两个染色体进行交叉pick=rand(1,2);while prod(pick)==0pick=rand(1,2);endindex=ceil(pick.*sizepop);% 交叉概率决定是否进行交叉pick=rand;while pick==0pick=rand;endif pick>pcrosscontinue;endflag=0;while flag==0% 随机选择交叉位置pick=rand;while pick==0pick=rand;endpos=ceil(pick.*sum(lenchrom)); %随机选择进行交叉的位置,即选择第几个变量进行交叉,注意:两个染色体交叉的位置相同pick=rand; %交叉开始v1=chrom(index(1),pos);v2=chrom(index(2),pos);chrom(index(1),pos)=pick*v2+(1-pick)*v1;chrom(index(2),pos)=pick*v1+(1-pick)*v2; %交叉结束flag1=test(lenchrom,bound,chrom(index(1),:)); %检验染色体1的可行性flag2=test(lenchrom,bound,chrom(index(2),:)); %检验染色体2的可行性if flag1*flag2==0flag=0;else flag=1;end %如果两个染色体不是都可行,则重新交叉end
end
ret=chrom;
2.2.4变异
function ret=Mutation(pmutation,lenchrom,chrom,sizepop,pop,bound)
% 本函数完成变异操作
% pcorss input : 变异概率
% lenchrom input : 染色体长度
% chrom input : 染色体群
% sizepop input : 种群规模
% pop input : 当前种群的进化代数和最大的进化代数信息
% ret output : 变异后的染色体for i=1:sizepop % 随机选择一个染色体进行变异pick=rand;while pick==0pick=rand;endindex=ceil(pick*sizepop);% 变异概率决定该轮循环是否进行变异pick=rand;if pick>pmutationcontinue;endflag=0;while flag==0% 变异位置pick=rand;while pick==0pick=rand;endpos=ceil(pick*sum(lenchrom)); %随机选择了染色体变异的位置,即选择了第pos个变量进行变异v=chrom(i,pos);v1=v-bound(pos,1);v2=bound(pos,2)-v;pick=rand; %变异开始if pick>0.5delta=v2*(1-pick^((1-pop(1)/pop(2))^2));chrom(i,pos)=v+delta;elsedelta=v1*(1-pick^((1-pop(1)/pop(2))^2));chrom(i,pos)=v-delta;end %变异结束flag=test(lenchrom,bound,chrom(i,:)); %检验染色体的可行性end
end
ret=chrom;2.2.5非线性规划fmincon函数
function ret = nonlinear(chrom,sizepop)for i=1:sizepopx=fmincon(inline('-5*sin(x(1))*sin(x(2))*sin(x(3))*sin(x(4))*sin(x(5))-sin(5*x(1))*sin(5*x(2))*sin(5*x(3))*sin(5*x(4))*sin(5*x(5))'),chrom(i,:)',[],[],[],[],[0 0 0 0 0],[2.8274 2.8274 2.8274 2.8274 2.8274]);ret(i,:)=x';
end2.2.6主程序
%% 清空环境
clc
clear
warning off%% 遗传算法参数
maxgen=30; %进化代数
sizepop=100; %种群规模
pcross=[0.6]; %交叉概率
pmutation=[0.01]; %变异概率
lenchrom=[1 1 1 1 1]; %变量字串长度
bound=[0 0.9*pi;0 0.9*pi;0 0.9*pi;0 0.9*pi;0 0.9*pi]; %变量范围%% 个体初始化
individuals=struct('fitness',zeros(1,sizepop), 'chrom',[]); %种群结构体
avgfitness=[]; %种群平均适应度
bestfitness=[]; %种群最佳适应度
bestchrom=[]; %适应度最好染色体
% 初始化种群
for i=1:sizepopindividuals.chrom(i,:)=Code(lenchrom,bound); %随机产生个体x=individuals.chrom(i,:);individuals.fitness(i)=fun(x); %个体适应度
end%找最好的染色体
[bestfitness bestindex]=min(individuals.fitness);
bestchrom=individuals.chrom(bestindex,:); %最好的染色体
avgfitness=sum(individuals.fitness)/sizepop; %染色体的平均适应度
% 记录每一代进化中最好的适应度和平均适应度
trace=[];%% 进化开始
for i=1:maxgen% 选择操作individuals=Select(individuals,sizepop);avgfitness=sum(individuals.fitness)/sizepop;% 交叉操作individuals.chrom=Cross(pcross,lenchrom,individuals.chrom,sizepop,bound);% 变异操作individuals.chrom=Mutation(pmutation,lenchrom,individuals.chrom,sizepop,[i maxgen],bound);%每进化10代,以所得值为初始值进行非线性寻优if mod(i,10)==0individuals.chrom=nonlinear(individuals.chrom,sizepop);end% 计算适应度for j=1:sizepopx=individuals.chrom(j,:);individuals.fitness(j)=fun(x);end%找到最小和最大适应度的染色体及它们在种群中的位置[newbestfitness,newbestindex]=min(individuals.fitness);[worestfitness,worestindex]=max(individuals.fitness);% 代替上一次进化中最好的染色体if bestfitness>newbestfitnessbestfitness=newbestfitness;bestchrom=individuals.chrom(newbestindex,:);endindividuals.chrom(worestindex,:)=bestchrom;individuals.fitness(worestindex)=bestfitness;avgfitness=sum(individuals.fitness)/sizepop;trace=[trace;avgfitness bestfitness]; %记录每一代进化中最好的适应度和平均适应度
end
%进化结束%% 结果显示
figure
[r c]=size(trace);
plot([1:r]',trace(:,1),'r-',[1:r]',trace(:,2),'b--');
title(['函数值曲线 ' '终止代数=' num2str(maxgen)],'fontsize',12);
xlabel('进化代数','fontsize',12);ylabel('函数值','fontsize',12);
legend('各代平均值','各代最佳值','fontsize',12);
ylim([1.5 8])
disp('函数值 变量');
% 窗口显示
disp([bestfitness x]);
grid on
2.2.6 运行结果

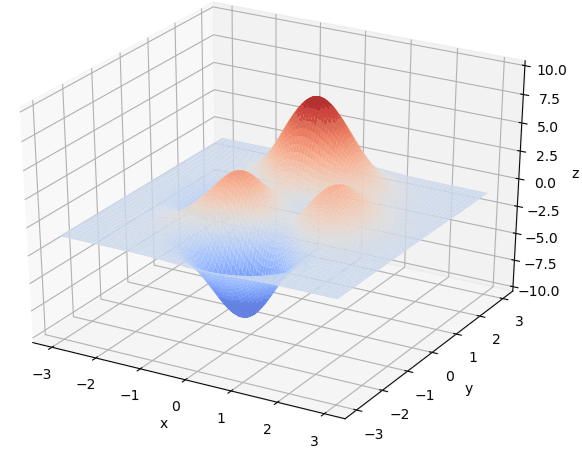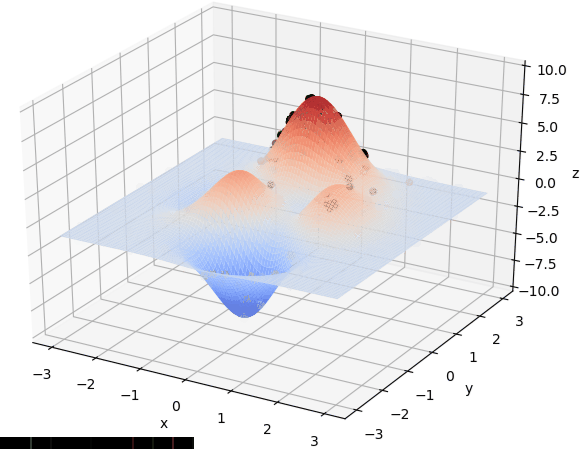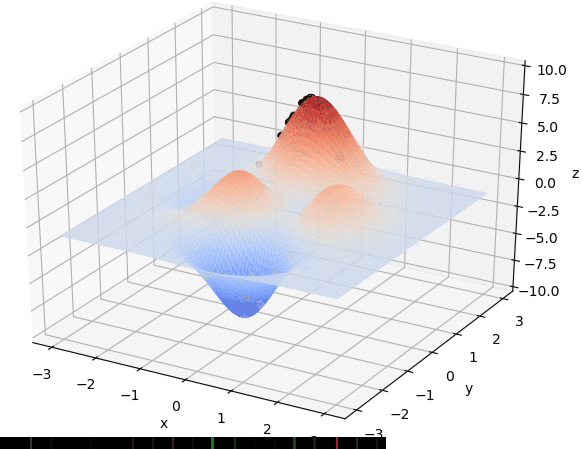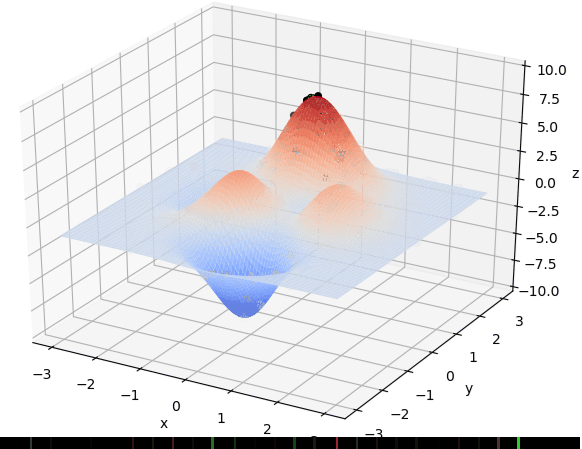
普通的遗传算法
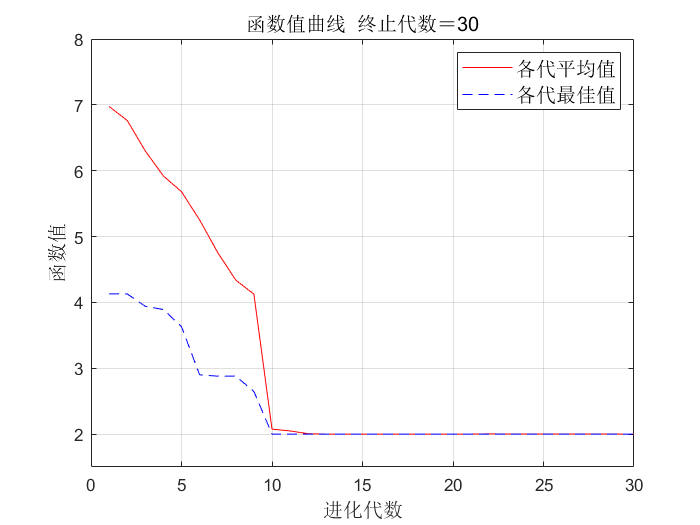
使用非线性规划函数fmincon的遗传算法
3.封装函数ga和gamultiobj的遗传算法
注:matlab的封装函数是求解最小值,如果需要求解最大值,有两个步骤:
①需要将适应度定义为目标函数的相反数
②将最后得到的目标函数值取反即可
3.1使用ga函数求最小值最大值
3.1.2例子①求最小值

ga函数的使用格式为:
x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,options)
其含义与fmincon函数同,这里不再赘述,对于options的更多选择可查看官网链接。
程序实现:
不等式约束(分文件编写):
function [c,ceq] = mynonlcon(x)
c = [];%无非线性不等式约束
ceq = x(1)^2+x(2)^2+x(3)^2-25;%非线性等式约束主函数:
clear all
clc
fitness = @(x)(1050-x(1)^2*x(2)^2-x(3)^2-x(1)*x(2)-x(1)*x(3));
options = gaoptimset('PopulationSize',25,...%种群大小
'CrossoverFraction',0.58,... %交叉率
'MigrationFraction',0.08,... %变异率
'PlotFcns',{@gaplotbestf,@gaplotbestindiv}); %绘制种群的平均适应度和最佳个体适应度
nvars = 3;%优化的变量个数
A = [];b = [];%没有线性不等式约束
Aeq = [9 13 7];beq = 63;%线性等式约束
lb = [0;0;0];ub = [inf;inf;inf];
nonlcon = @mynonlcon;
[x,fval] = ga(fitness,nvars,[],[],Aeq,beq,lb,ub,nonlcon,options)
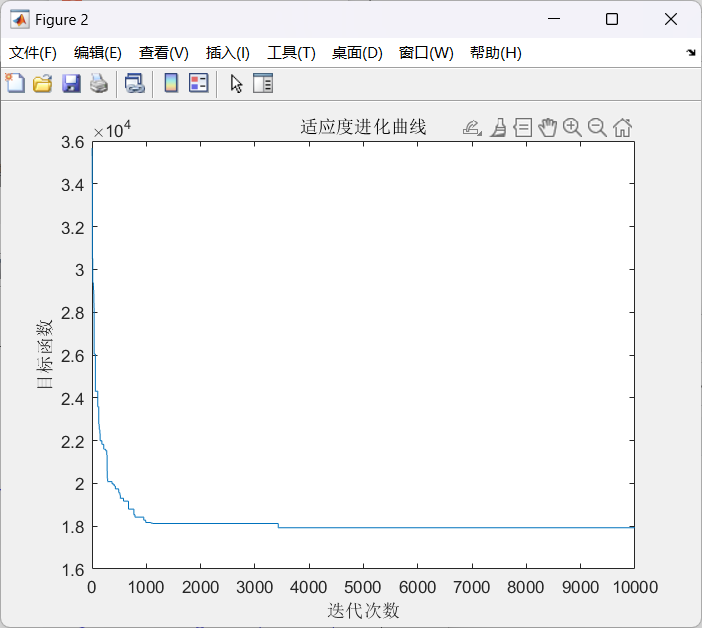
运行结果:
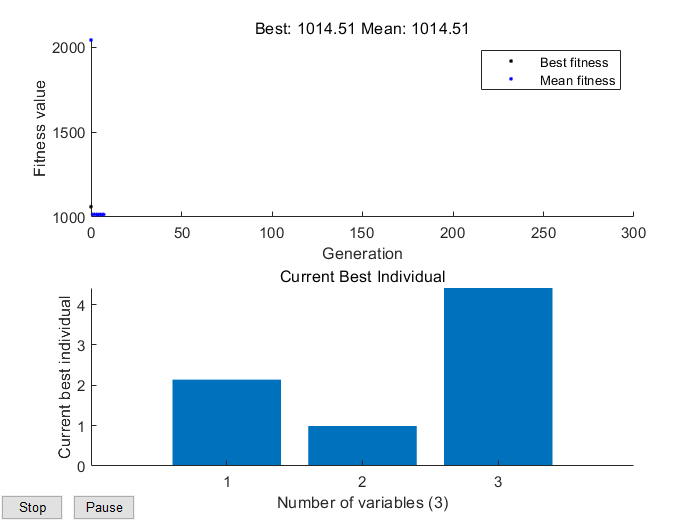
可以看到,迭代次数很小便已经找到了最小值:1014.51,其变量取值即当前最佳个体适应度大小。为了更形象的展示,下面举一个典型的一维例子来说明
3.1.2例子②求最小值

clear all
clc
fitness = @(x)(x+10*sin(5*x)+7*cos(4*x));
nvars = 1;%优化的变量个数
A = [];b = [];%没有线性不等式约束
Aeq = [];beq = [];%线性等式约束
lb = [0];ub = [9];
nonlcon = [];
options = gaoptimset('PopulationSize',50,...%种群大小 'CrossoverFraction',0.95,... %交叉率'MigrationFraction',0.08,... %变异率'Generations',20,'StallGenLimit',20,...'PlotFcns',{@gaplotbestf,@gaplotbestindiv});%绘制种群的平均适应度和最佳个体适应度
[x,fval] = ga(fitness,nvars,A,b,Aeq,beq,lb,ub,nonlcon,options)
figure(2)
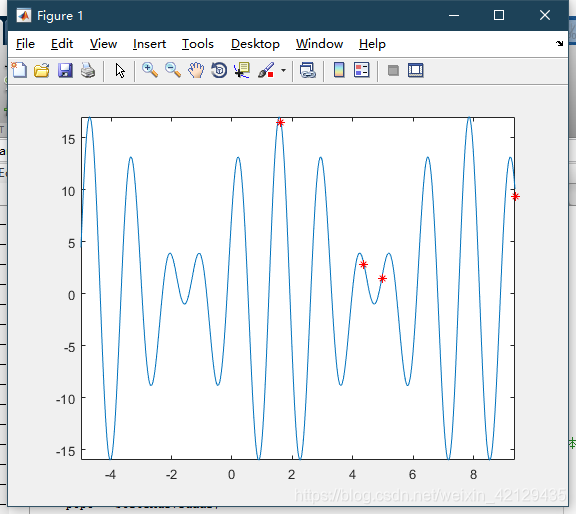
plot(x,fval,'*')%最优解
hold on
x = 0:0.1:9;
y = x+10*sin(5*x)+7*cos(4*x);
plot(x,y)%函数图像
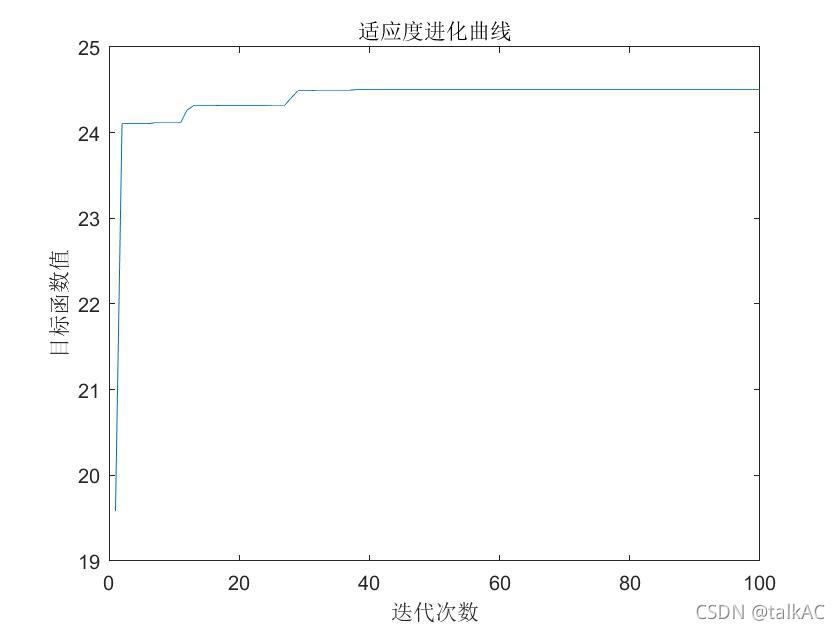
运行结果:
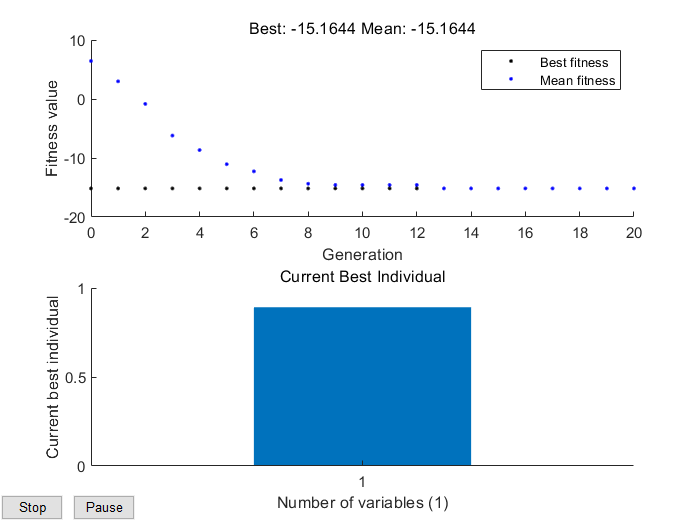
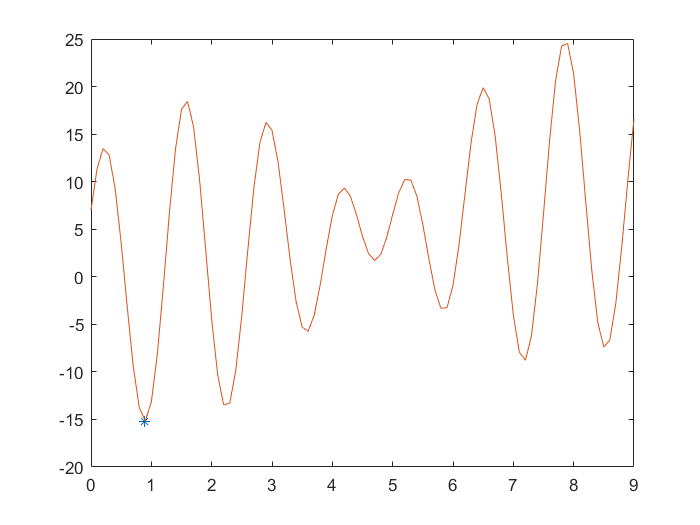
注:并非每次都能找到最优解,可能会陷入局部最优,解决的方法是①调整options、交叉和变异率;②多运行几次程序。
3.1.3例子②求最大值
为了便于比对和查看,仍选用3.2的例子,上述已经说了,matlab的封装函数库默认求最小值,如果求最大值,有两个步骤,一是将适应度函数取反,二是将优化后的目标值取反。
程序:
clear all
clc
fitness = @(x)-(x+10*sin(5*x)+7*cos(4*x));%适应度函数取为目标函数的相反数
nvars = 1;%优化的变量个数
A = [];b = [];%没有线性不等式约束
Aeq = [];beq = [];%线性等式约束
lb = [0];ub = [9];
nonlcon = [];
options = gaoptimset('PopulationSize',50,...%种群大小 'CrossoverFraction',0.95,... %交叉率'MigrationFraction',0.08,... %变异率'Generations',20,'StallGenLimit',20,...'PlotFcns',{@gaplotbestf,@gaplotbestindiv});%绘制种群的平均适应度和最佳个体适应度
[x,fval] = ga(fitness,nvars,A,b,Aeq,beq,lb,ub,nonlcon,options)
figure(2)
fval = -fval;%取反目标值
plot(x,fval,'*')%最优解
hold on
x = 0:0.1:9;
y = x+10*sin(5*x)+7*cos(4*x);
plot(x,y)%函数图像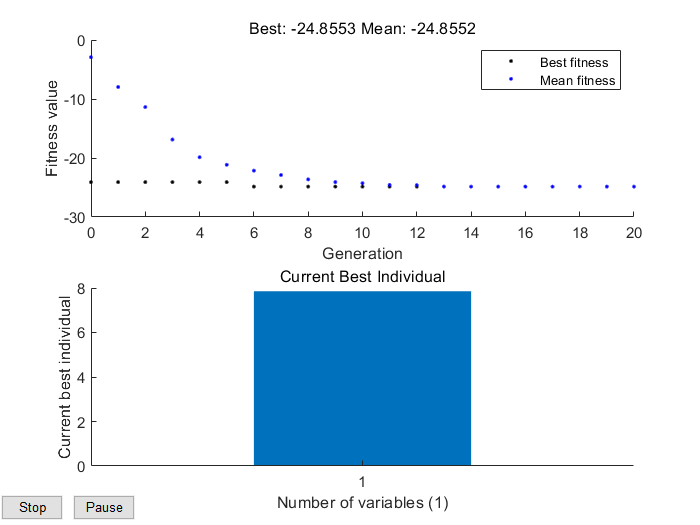
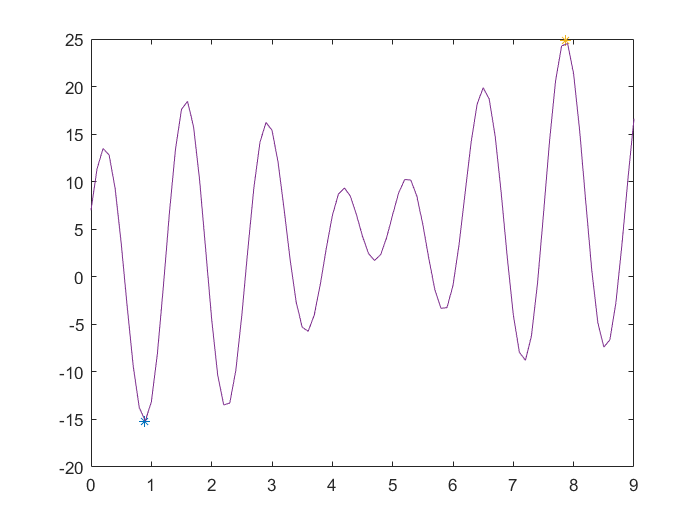
读者可以自行比对3.2和3.3的两个程序,对应上述两个步骤。
3.2使用gamultiobj函数求极值问题
gamultiobj函数从命名上便可以看出也是使用ga算法求解优化问题,只不过是针对多目标优化问题,其函数格式和ga同。
[ x,fval] = gamultiobj(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,options)
其解集形式是以pareto(帕累托)前沿呈现,我的理解就是最佳适应度曲线,也就是一组解集
那么什么叫pareto最优解呢?

对于这样的一个多目标函数,往往会出现f1和f2是相互矛盾的,即f1函数的提高会降低f2函数,称这样的解为非劣解,也就是所说的Pareto最优解,所以便有了多目标优化的算法。而gamultiobj就是基于带精英策略的快速非支配排序遗传算法(NSGA-II)。好了下面我们拿一个例子进行检验:
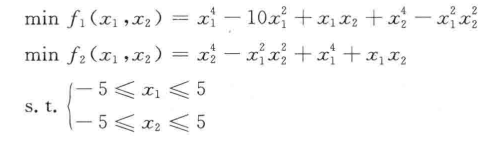
多目标适应度函数程序:
function f = fitness(x)
f(1) = x(1)^4-10*x(2)^2+x(1)*x(2)+x(2)^4-(x(1)^2)*(x(2)^2);
f(2) = x(2)^4-(x(1)^2)*(x(2)^2)+x(1)^4+x(1)*x(2);主文件:
clear all
clc
% f{1} = @(x)(x(1)^4-10*x(2)^2+x(1)*x(2)+x(2)^4-(x(1)^2)*(x(2)^2));
% f{2} = @(x)(x(2)^4-(x(1)^2)*(x(2)^2)+x(1)^4+x(1)*x(2));
% fitness = f; 不能使用匿名函数作为多目标函数优化的适应度函数
fitness = @fitness;
nvars = 2;%优化的变量个数
A = [];b = [];%没有线性不等式约束
Aeq = [];beq = [];%线性等式约束
lb = [-5 -5];ub = [5 5];
nonlcon = [];
%options = gaoptimset('ParetoFraction',0.3,'PopulationSize',100,'Generations',200,'StallGenLimit',200,'TolFun',1e-100,'PlotFcns',@gaplotpareto);options = gaoptimset('ParetoFraction',0.3,...'PopulationSize',100,...%种群大小'Generations',200,...'StallGenLimit',200,...'TolFun',1e-100,...'CrossoverFraction',0.58,... %交叉率'MigrationFraction',0.08,... %变异率'PlotFcns',{@gaplotbestf,@gaplotbestindiv,@gaplotpareto});%绘制Pareto解集
% 'PlotFcns',{@gaplotbestf,@gaplotbestindiv,@gaplotpareto}); %注不支持最佳个体和适应度曲线查看
[x,fval] = gamultiobj(fitness,nvars,A,b,Aeq,beq,lb,ub,options)
运行Pareto解集:
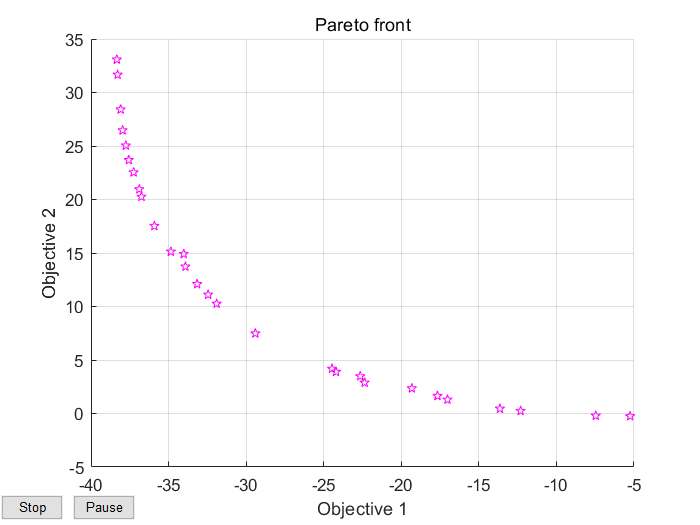
fval = -22.3634 2.8861
注:
①这里不方便使用匿名函数编写适应度函数,所以进行了分文件编写
②这里不能查看最佳个体和适应度曲线,详情见Optimization options

③对于2018以后的版本matlab会提示gaoptiset函数替换问题,其实只是函数更新问题,再后面加上注释:%#ok<GAOPT>即可,便不会提示。
④这个例子会超出迭代次数寻优,所以最优解不唯一,这里作为参照即可
4.optimtool工具箱的遗传算法实例介绍
这个工具箱包含了很多优化函数,其打开方式可以通过工具栏打开,也可以在命令行中输入:
optimtool或者optimtool('需要选用的优化函数'),如:optimtool('gamultiobj')
这里以上面gamultiobj的例题为参考,使用工具箱求解
下面展示和使用函数一样的设置:
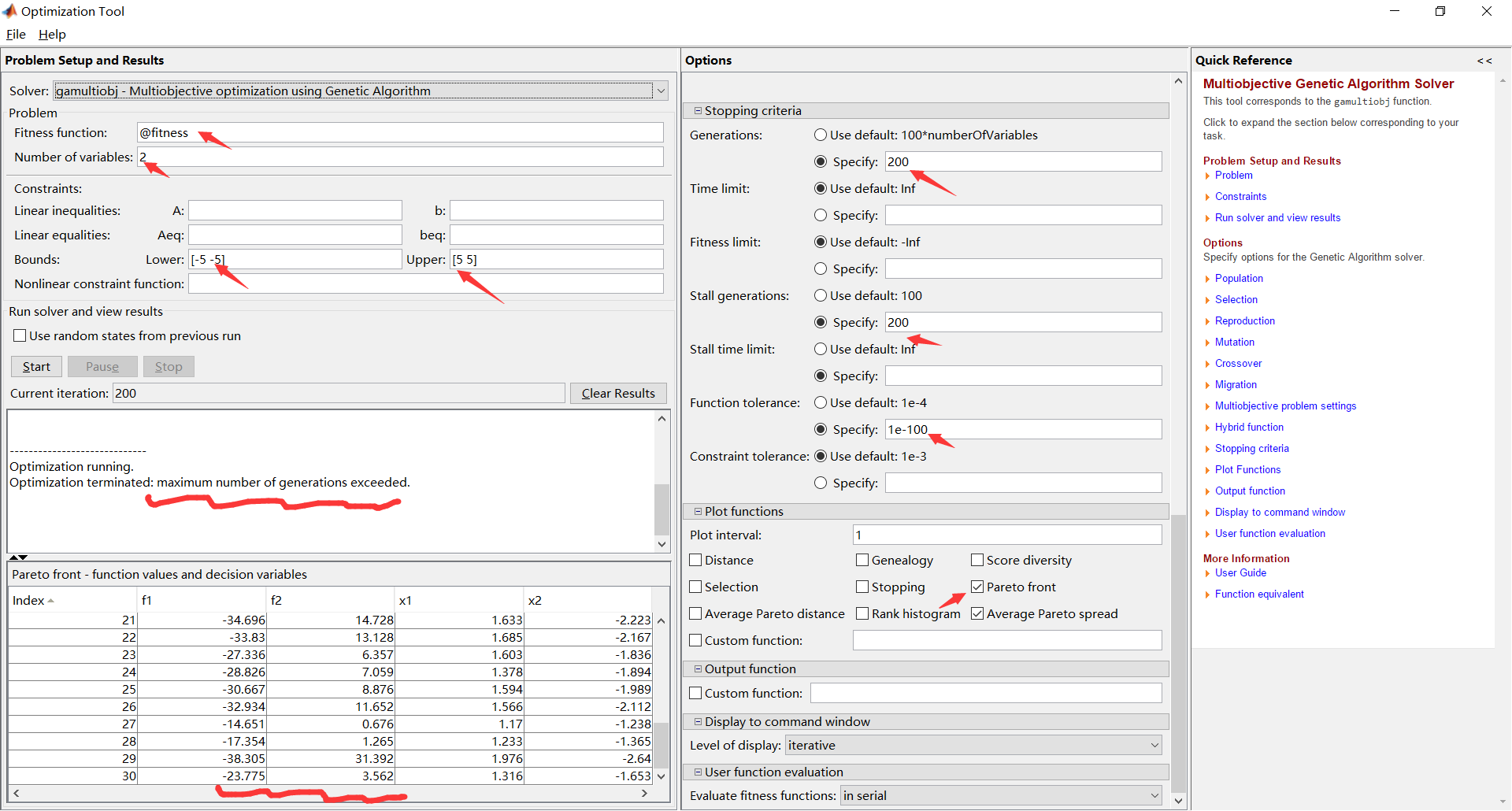
运行结果(这里勾选了两个出图):

5. 学习问题
①对于优化的遗传算法没有完全弄懂求最大和最小值
②对于封装函数求极大值时图像的绘制问题