遗传算法及实例

article/2025/11/6 22:39:37

        遗传算法是模拟生物在自然环境下遗传的过程而形成的自适应全局优化搜索算法。如果把某个问题的可行域看作是一个族群，目标函数看作是自然选择的条件，那么，这个族群通过一代又一代的繁衍和进化最终变成最接近筛选条件的样子。遗传算法就是利用了这个思想。

        在求解问题的过程中，将问题的可行解的全体看作是初始种群，目标函数作为适应度函数来进行筛选，通过一次又一次的迭代缩小可行解的范围，在该范围中确定最优解的位置。当然，这种方法得到的最优解往往都是最优解的近似或是局部的最优解，过于繁复的迭代也许也是它的一个缺点，但不可否认的是，遗传算法具有强大的适应性，它能够很好地解决各类问题，如大规模的优化问题，TSP问题等。

        使用遗传算法还有一个好处，或者说这类启发式算法都拥有的优势就是不需要清楚某一类问题具体的求解方法，它就是一种迭代过程，通过纯粹的迭代实现找到最优解的过程。以优化问题为例，通常的线性规划问题是通过单纯形法来求解，有着严谨的求解过程，而启发式算法则是通过一步又一步的迭代来实现这个过程。 

       遗传算法的核心步骤只有三个，一个是种群的选取，一个是“基因”的交叉，还有一个是基因的变异。其计算思路如下：

       1、选择初始种群

       2、计算适应度函数（目标函数），将其归一化后作为下一代选取的概率

       3、进行交叉操作（可以基于概率，也可以基于其他）

       4、进行变异操作

       5、重复2-4，直到达到循环条件（如迭代次数或误差小于某个值）

       以下为两个示例，第一个是通过遗传算法求解0-1规划问题；第二个是通过遗传算法求解TSP问题。 

%利用遗传算法求解目标规划问题
clear all;
close all;
clc;
c=[2 -1];%目标规划系数
A=-[5 4;-3 1];
b=-[20;3];
NP=500;%种群数目
L=length(c);%基因数目
Xs=20;%上限
Xx=0;%下限
G=1000;%最大遗传代数
Pc=0.8;%交叉概率
Pm=0.2;%变异概率
nf=zeros(NP,L);%储存子种群
f=randi([0,Xs],NP,L);%初始赋值
F=[];%储存可行解
count=0;
for k=1:Gcount=count+1;nn=0;for i=1:NPd(:,i)=A*f(i,:)';m=min(d(:,i)-b);if m>=0nn=nn+1;F(nn,:)=f(i,:);%筛选合适的种群endend%%%%%%%%%%%%%%%%%%将筛选合适的种群扩充%%%%%%%%%%%%%%%%%%%[aa,bb]=size(F);while aa<NPnnper=randperm(nn);if length(nnper)>=2AA=F(nnper(1),:);BB=F(nnper(2),:);elseAA=F(nnper(1),:);BB=F(nnper(1),:);endF=[F;AA;BB];[aa,bb]=size(F);endif aa>NP%保证种群数为NPF=F(1:NP,:);endf=F;for i=1:NPFit(i)=Hanshu(c,f(i,:));endMaxFit=max(Fit);MinFit=min(Fit);rr=find(Fit==MinFit);fBest=Fit(rr(1,1));xBest=f(rr(1,1),:);%%%%%%%%%%%%%%%%%%%%%%%%%交叉操作%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%for i=1:2:NPp=rand;if p<Pc%满足交叉条件q=randi([0,1],1,L);for j=1:Lif q(j)==1temp=nf(i+1,j);nf(i+1,j)=nf(i,j);nf(i,j)=temp;endendendend%%%%%%%%%%%%%%%%%%%%%%%变异操作%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%i=1;while i<=round(NP*Pm)h=randi([1,NP],1,1);%随机选取一个染色体for j=1:round(L*Pm)g=randi([1, L],1,1);%随机选取需要变异的基因nf(h,g)=0;endi=i+1;endf=nf;f(1,:)=xBest;trace(k)=MinFit;F=[];
end
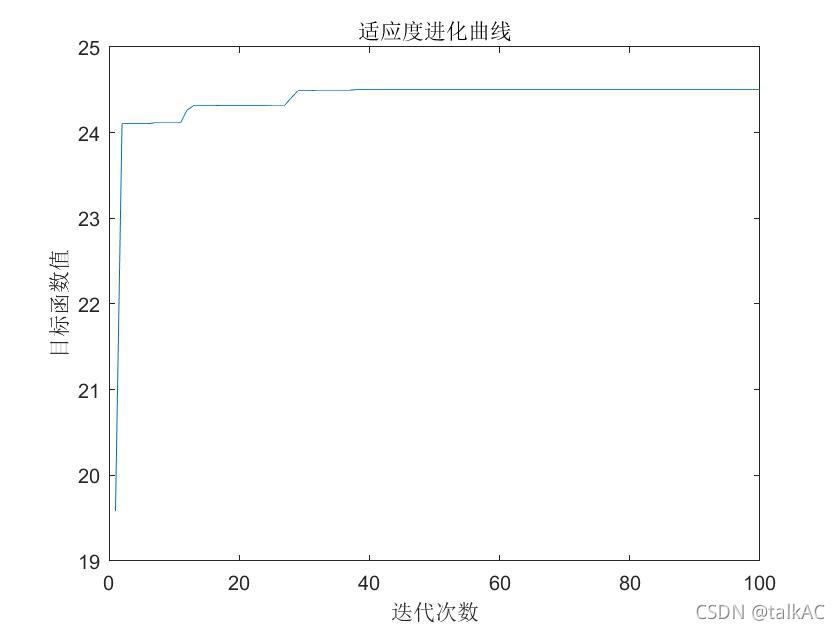
figure
xlabel('迭代次数');
ylabel('目标值函数');
title('适应度进化曲线');
plot(trace)
fBest
xBest
A*xBest'

         目标函数部为：

function result = Hanshu(f,x)
%HANSHU 此处显示有关此函数的摘要
%   此处显示详细说明
result=0;
for i=1:length(f)result=f(i)*x(i)+result;
end
end

       用MATLAB解决TSP问题代码如下：

​
%旅行商问题
%问题描述：
% 旅行商问题（TSP问题）。假设有一个旅行商人要拜访全国31个省会城市，
% 他需要选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最
% 后要回到原来出发的城市。对路径选择的要求是：所选路径的路程为所有路径
% 之中的最小值。
%全国31个省会城市的坐标为 
% [1304 2312；3639 1315；4177 2244；3712 1399；3488 1535；3326 1556；3238 1229；
% 4196 1004；4312 790；4386 570；3007 1970；2562 1756；2788 1491；2381 1676；1332 695；
% 3715 1678；3918 2179；4061 2370；3780 2212；3676 2578；4029 2838；4263 2931；3429 1908；
% 3507 2367；3394 2643；3439 3201；2935 3240；3140 3550；2545 2357；2778 2826；2370 2975]。%%%%%%%%%%%%%%%%%%%%%%%%%%遗传算法求解旅行商问题%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all
close all
clc;
C=[1304 2312;3639 1315;4177 2244;3712 1399;3488 1535;3326 1556;3238 1229;
4196 1004;4312 790;4386 570;3007 1970;2562 1756;2788 1491;2381 1676;1332 695;
3715 1678;3918 2179;4061 2370;3780 2212;3676 2578;4029 2838;4263 2931;3429 1908;
3507 2367;3394 2643;3439 3201;2935 3240;3140 3550;2545 2357;2778 2826;2370 2975];
NP=500;
N=31;%基因维数
G=10000;%迭代数
N=size(C,1);%城市个数
D=zeros(N);%任意城市间的距离矩阵
%计算城市间距离矩阵
for i=1:Nfor j=1:ND(i,j)=sqrt((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2);end
end
f=zeros(NP,N);%储存种群
for i=1:NPf(i,:)=randperm(N);
end
R=f(1,:);%储存最优种群
len=zeros(NP,1);%储存径路长度
fitness=zeros(NP,1);%储存归一化适应值
gen=0;%迭代次数
while gen<Gfor i=1:NPlen(i,1)=D(f(i,N),f(i,1));for j=1:(N-1)len(i,1)=len(i,1)+D(f(i,j),f(i,j+1));endendMaxlen=max(len);%最短路径Minlen=min(len);%最短路径%%%%%%%%%%%%%%%%%%%%更新最短路径%%%%%%%%%%%%%%%%%%%%%%rr=find(len==Minlen);R=f(rr(1,1),:);%%%%%%%%%%%%%%%%%%%计算归一化适应值%%%%%%%%%%%%%%%%%%%%for i=1:length(len)fitness(i,1)=-(len(i,1)-Maxlen)/(Maxlen-Minlen);end%%%%%%%%%%%%%%%%%%%%%选择操作%%%%%%%%%%%%%%%%%%%%%%%%%%nn=0;for i=1:NPif fitness(i,1)>=randnn=nn+1;F(nn,:)=f(i,:);endend[aa,bb]=size(F);while aa<NPnnper=randperm(nn);A=F(nnper(1),:);B=F(nnper(2),:);%%%%%%%%%%%%%%%%%%%%交叉操作%%%%%%%%%%%%%%%%%%%%%W=ceil(N/10);%交叉点个数p=unidrnd(N-W+1);%随机选择交叉范围，从p到p+Wfor i=1:Wx=find(A==B(p+i-1));y=find(B==A(p+i-1));temp=A(p+i-1);A(p+i-1)=B(p+i-1);B(p+i-1)=temp;temp=A(x);A(x)=B(y);B(y)=temp;end%%%%%%%%%%%%%%%%%%%%变异操作%%%%%%%%%%%%%%%%%%%%%p1=floor(1+N*rand());p2=floor(1+N*rand());while p1==p2p1=floor(1+N*rand());p2=floor(1+N*rand());endtmp=A(p1);A(p1)=A(p2);A(p2)=tmp;tmp=B(p1);B(p1)=B(p2);B(p2)=tmp;F=[F;A;B];[aa,bb]=size(F);endif aa>NPF=F(1:NP,:);endf=F;f(1,:)=R;F=[];gen=gen+1;Rlength(gen)=Minlen;
end
figure
for i=1:N-1plot([C(R(i),1),C(R(i+1),1)],[C(R(i),2),C(R(i+1),2)],'bo-');hold on;
end
title('最短化距离：',num2str(Minlen));
figure
plot(Rlength)
xlabel("迭代次数");
ylabel('目标函数');
title('适应度进化曲线');
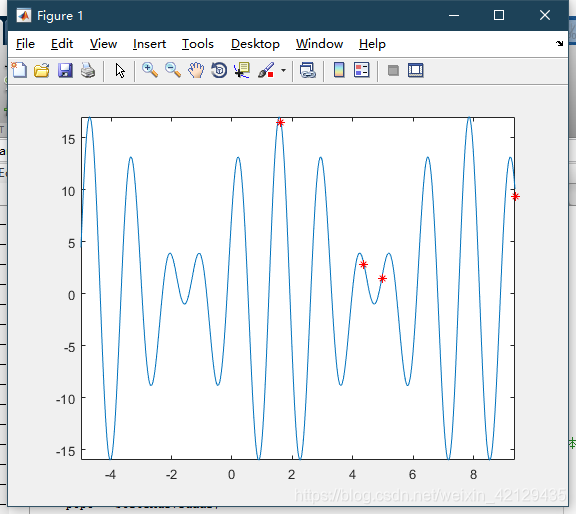
R​

         画出来的图稍显不靠谱的原因是因为计算长度没有考虑到第一个点与最后一个点之间的距离，运算结果如图所示：     

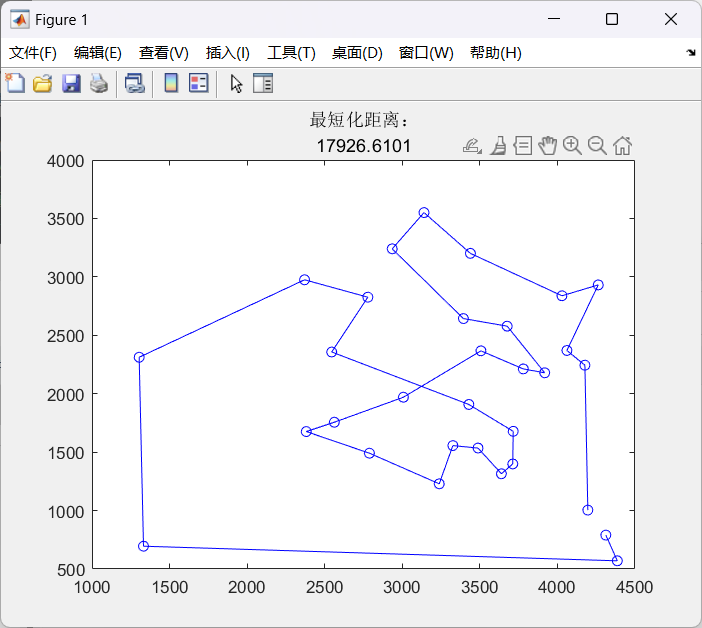
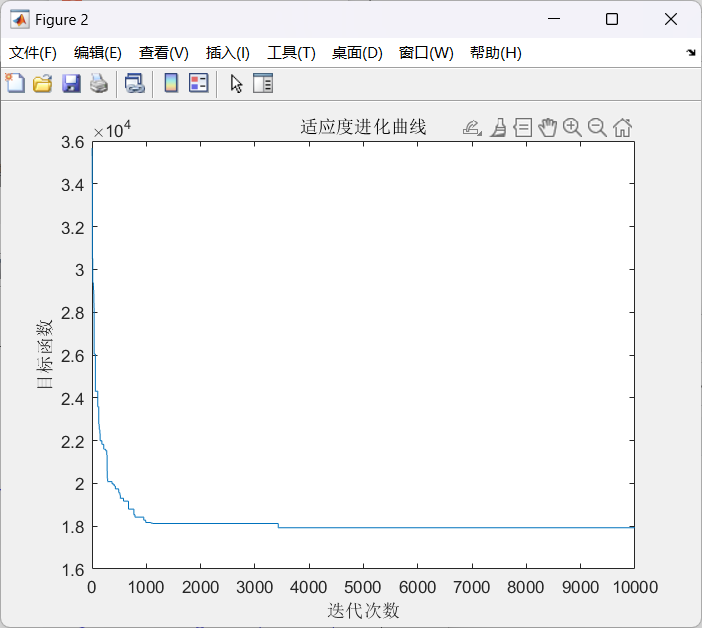
         由于我也是才开始接触这些算法（本科时没有参加建模接触这些还蛮可惜的），觉得很有意思的同时也深感需要学习的有很多，以及自己对这些算法的理解也稍显浅薄，如有不对之处还请指出。

参考：《智能优化算法及其MATLAB实例》——包子阳


http://chatgpt.dhexx.cn/article/gQu61DNC.shtml

相关文章

遗传算法原理及算法实例

遗传算法原理及算法实例

遗传算法原理解析 遗传算法&#xff08;GA&#xff09;是一种元启发式自然选择的过程&#xff0c;属于进化算法&#xff08;EA&#xff09;大类。遗传算法通常是利用生物启发算子&#xff0c;如变异、交叉和选择来生成高质量的优化和搜索问题的解决方案。 借鉴生物进化理论&…
阅读更多...
遗传算法小结及算法实例（附Matlab代码）

遗传算法小结及算法实例（附Matlab代码）

目录 1、遗传算法流程 2、关键参数说明 &#xff08;1&#xff09;群体规模 \(NP\) &#xff08;2&#xff09;交叉概率 \(P_c\) &#xff08;3&#xff09;变异概率 \(P_m\) &#xff08;4&#xff09;进化代数 \(G\) 3、MATLAB仿真实例 3.1 遗传算法求解一元函数的极…
阅读更多...
遗传算法（Genetic Algorithm,GA）实例详解

遗传算法（Genetic Algorithm,GA）实例详解

遗传算法是模拟生物在自然环境中的遗传和进化的过程而形成的自适应全局优化搜索算法&#xff0c;他能有效求解NP问题以及非线性、多峰函数优化和多目标优化问题。 1.理论基础 1.1生物学基础 遗传算法的生物学基础是借鉴了达尔文的进化论和孟德尔的遗传学说&#xff0c;一个种…
阅读更多...
遗传算法设计实例

遗传算法设计实例

1.遗传算法实例程序设计 随机初始化种群P(t){x1,x2…xn),计算P(t)中个体的适应值。其MATLAB程序的基本格式如下: Begin t0 初始化P(t) 计算P(t)的适应值; while (不满足停止准则)dobegintt1从P(t1)中选择P(t)重组P(t)计算P(t)的适应值 end例1 求函数 f(x) 9*sin(5x) cos(4x)…
阅读更多...
遗传算法GA原理详解及实例应用 附Python代码

遗传算法GA原理详解及实例应用 附Python代码

遗传算法GA 遗传算法&#xff08;Genetic Algorithm, GA&#xff09;是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型&#xff0c;是一种通过模拟自然进化过程搜索最优解的方法。 生物在自然界中的生存繁衍&#xff0c;显示了其对自然环境的优异的自适…
阅读更多...
vue实现点击下载exe，运行报错shellexecuteex失败 代码2

vue实现点击下载exe，运行报错shellexecuteex失败 代码2

页面效果 exe插件放在vue项目的public文件夹里&#xff0c;然后用a标签实现点击下载 <a href"/VideoWebPlugin.exe">下载插件</a> 成功下载后运行报错 解决方法&#xff1a;选择在文件夹中显示&#xff0c;右击属性&#xff0c;在兼容性设置里的以管理员…
阅读更多...
VC++分别使用WinExec、CreateProcess、ShellExecute和ShellExecuteEx来启动程序（附源码）

VC++分别使用WinExec、CreateProcess、ShellExecute和ShellExecuteEx来启动程序（附源码）

VC++常用功能开发汇总（专栏文章列表，欢迎订阅，持续更新...）https://blog.csdn.net/chenlycly/article/details/124272585C++软件异常排查从入门到精通系列教程（专栏文章列表，欢迎订阅，持续更新...）
阅读更多...
API函数ShellExecute与ShellExecuteEx用法

API函数ShellExecute与ShellExecuteEx用法

ShellExecute： 1.函数功能：你可以给它任何文件的名字，它都能识别出来并打开它。2．函数原型： HINSTANCE ShellExecute( HWND hwnd, LPCTSTR lpOperation, LPCTSTR lpFile, LPCTSTR lpParameters, LPCTSTR lpDirectory, INT nShowCmd ); 3．参数说明：hwnd:用于指定父窗口句…
阅读更多...
C/C++ 使用 API 函数 ShellExecuteEx 实现文件打印

C/C++ 使用 API 函数 ShellExecuteEx 实现文件打印

本文章主要介绍使用ShellExecuteEx实现打印文件的功能。 函数原型&#xff1a;BOOL ShellExecuteExA(__inout SHELLEXECUTEINFOA *pExecInfo) 输入输出参数都是 SHELLEXECUTEINFO 结构体。 SHELLEXECUTEINFO定义&#xff1a; typedef struct _SHELLEXECUTEINFO { DWORD c…
阅读更多...
Windows函数 ShellExecuteEx

Windows函数 ShellExecuteEx

点击进入视频教程 代码&#xff1a; #include<windows.h> #include<tchar.h> #pragma comment(lib, "Urlmon.lib") int WINAPI _tWinMain(HINSTANCE hinstance, HINSTANCE hPreInstance, LPTSTR lpCmdLine, int nShowCmd) {// 下载图片&#xff0c;并保…
阅读更多...
UpdatePanel终于可以上传文件了！

UpdatePanel终于可以上传文件了！

我们要做的&#xff0c;只是在页面上添加一个控件而已。 不过&#xff0c;其实这只是个半成品&#xff0c;或者说是一个原型&#xff0c;但是很明显&#xff0c;我们做对了。:) 在实现上&#xff0c;我曾经在两个做法上斟酌了许久&#xff0c;第一种是继承ScriptManager&#x…
阅读更多...
updatepanel 排版问题

updatepanel 排版问题

使用 ASP.NET AJAX 開發人員&#xff0c;一定不會錯過 UpdatePanel 這個超級控制項&#xff0c;它可以讓輕易的讓原有設計的頁面很輕易的具有 AJAX 的效果。可是在設計階段使用 UpdatePanel 去排版常造成我們的困擾&#xff0c;放置在 UpdatePanel 中的控制項無法正確呈現實際的…
阅读更多...
学习UpdatePanel控件-

学习UpdatePanel控件-

原文可以显示图片&#xff08;转载&#xff1a;http://blog.csdn.net/ILOVEMSDN/archive/2007/11/11/1879343.aspx&#xff09; UpdatePanel控件的使用 2008-10-07 05:46 P.M. ScriptManager和UpdatePanel控件联合使用可以实现页面异步局部更新的效果。其中的UpdatePanel就是…
阅读更多...
UpdatePanel的用法

UpdatePanel的用法

UpdatePanel控件也是Ajax里用得最多的控件之中的一个&#xff0c;UpdatePanel控件是用来局部更新网页上的内容&#xff0c;网页上要局部更新的内容必须放在UpdatePanel控件里&#xff0c;他必须和上一次说的ScriptManager控件一起使用。如今来看UpdatePanel的属性 UpdatePanel …
阅读更多...
浅谈UpdatePanel

浅谈UpdatePanel

这是我以前刚学习asp.net ajax的时候总结的&#xff0c;如果有什么错误的地方&#xff0c;请大家指出&#xff0c;以便我能早日改正。 1. 作用&#xff1a; UpdatePanel控件用来控制页面的局部更新&#xff0c;这些更新依赖于ScriptManager的EnablePartialRendering属性&…
阅读更多...
UpdatePanel 控件简介

UpdatePanel 控件简介

UpdatePanel 控件简介 全部折叠全部展开 代码&#xff1a;全部 代码&#xff1a;多种 代码&#xff1a;Visual Basic 代码&#xff1a;C# 代码&#xff1a;Visual C 代码&#xff1a;F# 代码&#xff1a;JScript UpdatePanel 控件简介 在本教程中&#xff0c;您将使用两…
阅读更多...
ScriptManager updatepanel

ScriptManager updatepanel

在项目开发中&#xff0c;遇到了一个ajax更新问题&#xff0c;母版上有个通知区域&#xff08;通知区域为ajax定时更新&#xff08;updatepanel&#xff09;&#xff09;&#xff0c;上面有需要显示的几列信息&#xff0c;如最新文章数&#xff0c;批阅数&#xff0c;FTP受信状…
阅读更多...
使用 UpdatePanel

使用 UpdatePanel

1 概述 ASP.NET UpdatePanel 控件能让你创建丰富的、以客户为中心的 Web 应用程序。使用 UpdatePanel 控件&#xff0c;可以刷新选择的页面部分而不是使用回发来刷新整个页面&#xff0c;这就像是执行了一个局部页面更新一样。包含一个 ScriptManager 和一个或多个 UpdatePanel…
阅读更多...
UpdatePanel控件

UpdatePanel控件

ASP.NET UpdatePanel控件可用于生成功能丰富、以客户端为中心的Web应用程序。通过使用UpdatePanel控件&#xff0c;可以在回发期间刷新网页的选定部分而不是刷新整个网页。这称为执行部分页更新。包含一个ScriptManager控件和一个或多个UpdatePanel控件的ASP.NET网页&#xff0…
阅读更多...
ASP.NET AJAX入门系列（4）：使用UpdatePanel控件（一）

ASP.NET AJAX入门系列（4）：使用UpdatePanel控件（一）

UpdatePanel可以用来创建丰富的局部更新Web应用程序&#xff0c;它是ASP.NET 2.0 AJAX Extensions中很重要的一个控件&#xff0c;其强大之处在于不用编写任何客户端脚本&#xff0c;只要在一个页面上添加几个UpdatePanel控件和一个ScriptManager控件就可以自动实现局部更新。通…
阅读更多...
推荐文章

Copyright @ 2022~2023