Mininet笔记-基本命令

article/2025/9/19 22:15:39

命令详解拓扑构建命令

在这里插入图片描述

–topo

在这里插入图片描述

 单一（single）拓扑，永远只有一个交换机，主机（host）可以有N个
 线形（linear）拓扑，可以有多个交换机和主机，每个交换机只连接一台主机，交换机之间线性相连

在这里插入图片描述

 树形（tree）拓扑，深度depth=2，指的是交换机的深度为2，也即两层的交换机。扇出fanout=2指的是一个交换机下挂两个设备（子树的个数）。第一层交换机永远只有一个
 自定义（custom）拓扑，执行我们自己用python编写的脚本文件。此时的file.py已经在custom目录下，使用的是相对路径。Mytopo是file文件里定义好的类

–switch 交换机

在这里插入图片描述
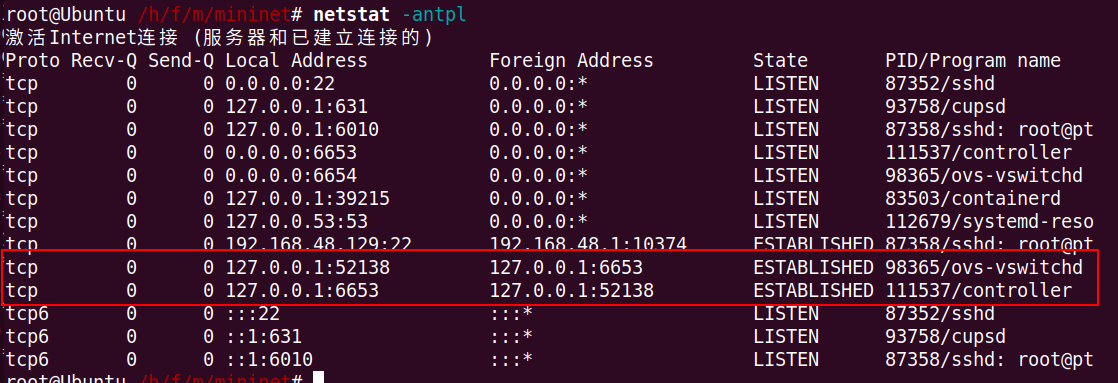
Mininet的控制器有时候会被关掉，需要指定远程控制器来使用。
处于用户态的交换机：所有进程访问的空间内存对象受限，可被抢占机制
处于内核态：可访问所有内存空间和对象。不可被抢占机制

–controller

在这里插入图片描述

–mac

在这里插入图片描述

如果不指定，就会每次mn命令创建拓扑的时候自动生成。不好记忆
内部交互命令

内部交互命令

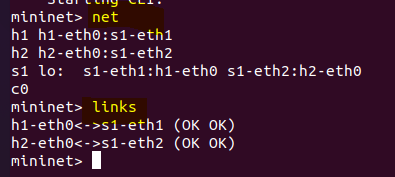
Net

在这里插入图片描述

查看网络信息，链路信息
在这里插入图片描述
创建了两个主机host1和host2，创建了一个交换机s1。两个主机与交换机相连，即一个交换机下挂两个主机

Nodes

查看可用节点
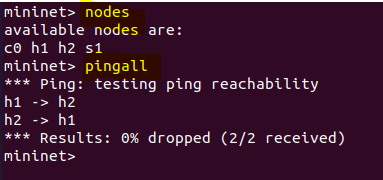
在这里插入图片描述

Links

查看链路健壮性
在这里插入图片描述

Pingall

查看所有节点间的连通性
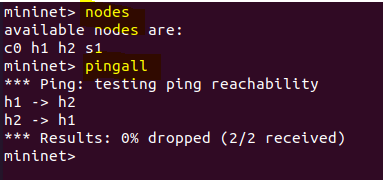
在这里插入图片描述
0% dropped：无丢包

mininet> py net.addHost('h3')	//添加h3节点
<Host h3:  pid=29158> 
mininet> py net.addLink(s1,net.get('h3')) //将h3与s1节点连接起来
<mininet.link.Link object at 0x7f199af28e80>
//此时还不能实现h3和s1相连通
mininet> py s1.attach('s1-eth3')	//在s1为h3设置一个网络接口
mininet> py net.get('h3').cmd('ifconfig h3-eth0 10.3')	//给h3设置了ip地址，其实根本不知道10.3是不是与前面的连续…mininet> dump	//查看所有主机的情况
<Host h1: h1-eth0:10.0.0.1 pid=28831> 
<Host h2: h2-eth0:10.0.0.2 pid=28833> 
<Host h3: h3-eth0:None pid=29158> //h3，我们设置了ip地址但是还没有被查看到，原因是，因为主机之间还没有互相ping过，没有发现h3的ip地址
<OVSSwitch s1: lo:127.0.0.1,s1-eth1:None,s1-eth2:None,s1-eth3:None pid=28838> 
<Controller c0: 127.0.0.1:6653 pid=28824> 
mininet>//所以让随便一个主机来ping h3
ininet> h1 ping h3//就比如h1 ping h3
PING 10.0.0.3 (10.0.0.3) 56(84) bytes of data.
64 bytes from 10.0.0.3: icmp_seq=1 ttl=64 time=5.55 ms
64 bytes from 10.0.0.3: icmp_seq=2 ttl=64 time=0.392 ms
64 bytes from 10.0.0.3: icmp_seq=3 ttl=64 time=0.214 ms
64 bytes from 10.0.0.3: icmp_seq=4 ttl=64 time=0.068 ms
64 bytes from 10.0.0.3: icmp_seq=5 ttl=64 time=0.795 ms
64 bytes from 10.0.0.3: icmp_seq=6 ttl=64 time=0.058 ms
64 bytes from 10.0.0.3: icmp_seq=7 ttl=64 time=0.068 ms
64 bytes from 10.0.0.3: icmp_seq=8 ttl=64 time=0.049 ms
64 bytes from 10.0.0.3: icmp_seq=9 ttl=64 time=0.079 ms
64 bytes from 10.0.0.3: icmp_seq=10 ttl=64 time=0.059 ms
64 bytes from 10.0.0.3: icmp_seq=11 ttl=64 time=0.052 ms
64 bytes from 10.0.0.3: icmp_seq=12 ttl=64 time=0.093 ms
^C
--- 10.0.0.3 ping statistics ---
12 packets transmitted, 12 received, 0% packet loss, time 11246ms
rtt min/avg/max/mdev = 0.049/0.623/5.551/1.500 ms
//ping成功说明h3是有ip地址存在的
//再次dump，就有了h3的ip地址：
mininet> dump
<Host h1: h1-eth0:10.0.0.1 pid=28831> 
<Host h2: h2-eth0:10.0.0.2 pid=28833> 
<Host h3: h3-eth0:10.0.0.3 pid=29158> 
<OVSSwitch s1: lo:127.0.0.1,s1-eth1:None,s1-eth2:None,s1-eth3:None pid=28838> 
<Controller c0: 127.0.0.1:6653 pid=28824> 
mininet>