1、背景

近年来，为推进我国储能技术朝着商业化应用发展，国家出台了多项政策。从现有政策解读可知，虽然国家鼓励在用户侧建设分布式储能系统，但暂未出台针对用户侧电池储能的充放电标杆电价、容量补贴细则、充放电补贴细则、用户容量费抵扣细则等；配用电侧的电力现货市场和用户侧参与辅助服务市场等方面的市场机制尚未真正建立，用户侧投资建设的储能在此外部环境下仅能通过削峰填谷,从峰谷电价差中套利。

图1：储能应用于削峰填谷

目前，全国用电大省的峰谷价差区间为0.4-0.9元/kWh。据统计，2018年全社会用电量排名前二的省份是广东和江苏，用电量分别为5958.97亿千瓦时和5807.89亿千瓦时。而其峰谷价差均高于0.8元/kWh，为用户侧储能的峰谷价差套利提供了空间。

在用户侧安装电池储能系统常见的有3种应用模式，分别是离网型自发自用系统、并网型负荷+储能系统和并网型光伏+储能系统。

离网型自发自用系统是一个独立的解决方案，适用于没有并网或并网电力不稳定地区，重点解决无电区人口用电和海岛供电问题，安装储能装置用以保障用户供电的持续性，减少高成本低负载的线路建设投资。

并网型负荷+储能系统是指单纯通过储能电池的充放电过程调节用户用电曲线，实现削峰填谷的电池储能系统。从用户价值角度讲，可通过峰谷价差实现套利、减少用户配电变压配置容量和负载损耗、降低停电损失。

并网型光伏+储能系统在光伏发电基础上使用储能电池作为机动资源，提升自用比例。在光伏发电量多于系统消纳时，储存盈余电量，并在光伏发电量不足时放电。过滤光伏发电的波动性，提升用电质量和可靠性。通过建立适当的能源调度模型，进行更为高效的削峰填谷。

本报告主要探讨并网型负荷+储能系统的应用模式，具体而言，负荷主要是充电桩，使用场景为储能充电站。

2、储能削峰填谷方案设计

储能用于充电站的应用场景主要有两种方式，一种是分布式，即在每台充电桩各配置一定容量的梯次储能电池，这种方式不需要储能逆变器，但需采用兼容直流输入的充电模块，充电桩结构设计得为储能电池留出空间，另外，直流输入还可能涉及断路器、输入接触器等器件的重新选型；另一种是集中式，即整个场站配置储能电池，这种方式需要储能逆变器，将储能逆变器的直流输出变成交流电接到充电桩输入端。比较而言，一方面集中式的储能循环利用效率更高，更便于集中管理，在储能集装箱中配置空调系统，改善电池工况；另一方面不涉及充电桩器件的重新选型和结构的变动，因此本方案采用集中式的储能方式。

图2为储能充电站的系统架构，通常而言，该系统架构都支持光伏等清洁能源的接入。光伏接入仅需额外投入太阳能电池板，通常而言，充电站都能及时消耗光伏发电，极少存在“弃光”现象。据扬州示范场站的反馈，光伏的回收期仅需要3年，显著短于储能的回收期5~7年，因此，储能充电站通常都会接入光伏，形成“光储充”一体化场站。

但因为光伏容量有限（常规场站雨棚顶部配置太阳能电池板规模通常在100kW左右），相比储能电池MW级别而言可以忽略，因此，本报告不对其进行测算。

图2 储能充电站系统架构

3、储能系统投资收益静态测算

3.1 储能电池容量计算

如果想充分利用储能设备，尽快收回投资，则应按最小需求容量配置储能电池（不考虑电池的衰减），此时电池在一年中各月都满负荷运行，季差容量利用率为100%。以江苏某场站今年截至9月每月用电情况为例分析，可通过以下公式计算储能电池需求容量。

储能电池容量=日均峰时用电量/(充放电深度×电池效率×逆变器效率)

图3 储能电池容量需求计算（设每周用电6日）

从用电负荷来看，在不同的季节用电行为有较大差别，最大需求容量是最小需求容量的3倍。如果想充分利用储能设备，尽快收回投资，则应按最小需求容量配置储能电池（不考虑电池的衰减）。在此算例中，最小需求容量为1458kWh，取1500kWh作为建设容量。此时电池在一年中各月都满负荷运行，季差容量利用率为100%。

3.2 储能电池充放电量计算

储能电池的年衰减系数以0.03计算，随着使用年数i增加，电池容量的剩余比率降低。

江苏省的峰谷电价曲线为两峰一谷，由图1可知，每天最多可完成“谷峰”+“平峰”两次循环，但考虑到“平峰”不一定能完成一个完整的循环，因此需要乘以一个平峰折算系数，该系数介于0~1之间，当平峰折算系数取0时，即表示每天只进行“谷峰”循环。

则，

当年谷时充电量=电池剩余容量×年循环次数×DOD电池放电深度×季差容量利用率

当年峰时放电量1=当年谷时充电量×电池充放电效率×逆变器效率

当年平时充电量=当年谷时充电量×平峰折算系数

当年峰时放电量2=当年峰时放电量1×平峰折算系数

3.3 储能系统投资成本及每年收益

电池储能系统的成本主要包含电池的容量成本、逆变器成本和系统的维护成本。容量成本设定为900元/kWh。逆变器成本设定为600元/kWh。系统维护费用设定为5000元/年。

初期建设总成本=建设容量×（电池单位成本+逆变器单位成本）

当年收益=（峰价×当年峰时放电量1-谷价×当年谷时充电量）+平峰折算系数×（峰价×当年峰时放电量1-平价×当年谷时充电量）

3.4 储能系统投资收益静态测算

设定的测算条件如下：

建设总容量1500kWh，初期建设总成本按每瓦1.5元计；
电池循环深度按90%计；
每年运行按330天计，平峰折算系数设定为0.5，即每年完成330个谷峰循环+330*0.5个平峰循环；
峰谷价差0.8元，平谷价差0.3元计。

结果如图4所示，从图4可以看出，当前阶段，储能回收期在6~7年左右。

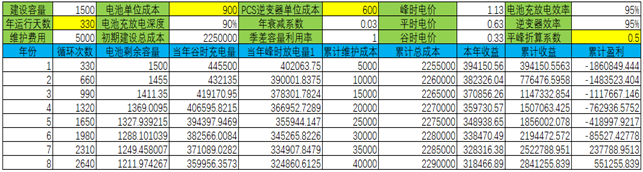
图4 常规条件下的储能投收益测算结果

当前及未来一段时间，电池充放电效率、逆变器效率、电池年衰减系数、电池充放电深度、维护成本不会有太大变化，当储能电池容量按最小需求容量配置时，季差容量利用率等于1，在峰平谷电价一定的条件下，对投资收益影响较大的因素主要有：年运行天数、初期建设单位成本（电池单位成本+PCS逆变器单位成本）、平峰折算系数，如上图黄色标注所示。

3.5 初期建设单位成本的考察

设定测算条件如下，考察初期建设单位成本：

（1）建设总容量1500kWh；

（2）电池循环深度按90%计；

（3）每年运行按330天计，平峰折算系数设定为0.5，即每年完成330个谷峰循环+330*0.5个平峰循环；4.2

（4）峰谷价差0.8元，平谷价差0.3元计。

结果如下：

（1）初期建设单位成本为1.5元/瓦时，初期建设总成本225万，回收期6~7年；

（2）初期建设单位成本为1.3元/瓦时，初期建设总成本，回收期5~6年；

（3）初期建设单位成本为1.1元/瓦时，回收期4~5年；

上述条件下，初期建设成本为1.2元/瓦时，项目回收期正好在5年左右，如图5所示。

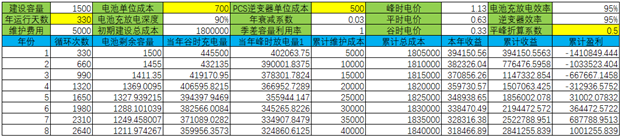
图5 初期建设成本降至1.2元/瓦时的储能投资收益测算结果

4、储能系统投资收益静态测算的数学模型

4.1 最简单的数学模型

不考虑电池容量随时间的衰减，忽略每年的维护成本，假定每年的电价（峰时电价、谷时电价、平时电价）相同，假定每年的运行状况（运行天数，平峰折算系数）相同，则

累计收益y1：

y1=k1*a*t

其中，

t表示运行年份；

a表示系统建设容量；

k1表示单位容量的电池每年产生的收益；

在上述假定条件下，k1、a都是常量，累计收益是时间t的一次函数。

投入总成本y0：

y0=k0*a

其中，

a表示系统建设容量；

k0表示初期建设每瓦单位成本；

投入总成本是时间t的常量函数。

图6 储能投入总成本及累计收益曲线图

项目回收年限t

可通过方程
y1=y0

求解。

即：

k1*a*t=k0*a

也就是图6中两条直线交叉的年限t。从上面的方程可以看出，在不考虑电池容量随时间的衰减，忽略每年的维护成本，假定每年的电价（峰时电价、谷时电价、平时电价）相同，假定每年的运行状况（运行天数，平峰折算系数）相同的条件下，储能项目的回收期与投建规模无关。

4.2 各因素的影响

如图7所示，随着初期建设每瓦单位成本的下降，投入总成本曲线向下平移，项目回收期会缩短。

图7 初期建设单位成本下降的影响

其余条件与最简单的数学模型相同，但考虑电池容量随时间的衰减，如图8所示，累计收益曲线逐渐向下偏离最简单数学模型的累计收益曲线，项目回收年限变长。

图8 电池容量衰减的影响

再考虑每年的维护成本，如图9所示，储能投入总成本会随着时间略微上翘，但MW级别的充电站，维护成本仅占投入总成本很小的比例，虽然其会延长项目回收年限，但影响可以忽略不计。

另外，一个很显然的事实是，随着系统建站容量的减小，维护成本对项目回收年限的影响会逐渐增大。

图9 电池容量衰减叠加维护成本的影响

峰、平、谷电价差会影响最简单数学模型中累计收益直线的斜率。

每年运行天数、平峰折算系数的变化会影响横向坐标，在最简单的数学模型中也可以看作对累计收益直线斜率的影响。

5、静态测算存在的问题及解决

上面储能系统投资收益的静态测算，并未考虑负荷端用电成本对充电需求的影响，对于自用电且用电需求不能在峰、平、谷之间转移的情形是没有问题的。

但通常来说，用电成本的上升会抑制充电需求。只有在用电成本（服务费+峰、平、谷电价）的变化对充电需求没有影响或影响很小的前提下，上述分析才有意义。如果充电成本的上升抑制了峰时充电需求，那么项目回收期会变长。

那么怎么解决这个问题呢？

前面储能电池容量计算的时候提到，如果想充分利用储能设备，尽快收回投资，则应按最小需求容量配置储能电池（不考虑电池的衰减），此时电池在一年中各月都满负荷运行。

可以看出，为了保证电池在一年中各月都满负荷运行，计算储能电池容量的时候，得考虑用电成本（服务费+峰、平、谷电价）的变化对充电需求的影响。因此，实际用于计算的峰时用电量，得考虑用电成本变化造成的影响。

6、分析总结

简单做一下回顾。

如图5所示，电池循环深度按90%计，每年完成330个谷峰循环+330*0.5个平峰循环，峰谷价差0.8元、平谷价差0.3元，初期建设单位成本为1.2元/瓦的条件下，项目回收期正好在5年左右。
从最简单的数学模型可知道，在不考虑电池容量随时间的衰减，忽略每年的维护成本，假定每年的电价（峰时电价、谷时电价、平时电价）相同，假定每年的运行状况（运行天数，平峰折算系数）相同的条件下，储能项目的回收期与投建规模无关。
如图7所示，在最简单的数学模型中，随着初期建设每瓦单位成本的下降，投入总成本曲线向下平移，项目回收期会缩短。
其余条件与最简单的数学模型相同，但考虑电池容量随时间的衰减，如图8所示，累计收益曲线逐渐向下偏离最简单数学模型的累计收益曲线，项目回收年限变长。
再考虑每年的维护成本，如图9所示，储能投入总成本会随着时间略微上翘，但MW级别的充电站，维护成本仅占投入总成本很小的比例，虽然其会延长项目回收年限，但影响可以忽略不计。
另外，一个很显然的事实是，随着系统建站容量的减小，维护成本对项目回收年限的影响会逐渐增大。
峰、平、谷电价差会影响最简单数学模型中累计收益直线的斜率。每年运行天数、平峰折算系数的变化会影响横向坐标，在最简单的数学模型中也可以看作对累计收益直线斜率的影响。

如果以回收期5年来考察项目是否施行，其实是有很多挑战的。

首先，初期建设单位成本能否控制在1.2元/瓦以内。
每年能否完成超过330个谷峰循环+330*0.5个平峰循环。
循环深度能否达到90%以上。

推论及个人观点：

现在充电客户的用电成本在一天内按统一电价执行，若后期定价存在峰、平、谷差异，需要考虑负荷在一天内不同时段的转移，只能按照测算出的高峰期的刚性负荷的充电量去计算建站容量，不宜过高估计建站容量，否则高峰期的弹性负荷一旦转移，每天循环深度就达不到设计值，进而拉长项目回收期。
建站容量过高存在拉长项目回收期的风险，另一方面达到一定规模后（如MW级别）项目回收期与投建规模无关，因此，个人建议按照相对较小的规模投建充电站的储能项目。
充电站的储能项目接入光伏，因为其回收期更短。
储能充电站能建立跟常规充电站的成本比较优势，为制定充电定价策略占领更大市场留出了空间。
当前储能项目只是在赢利平衡点附近，项目回收都考验着设计、建设、运营等各个环节，不具备大规模推广的基础，但随着新能源汽车的大力推广，单瓦电池成本是会显著下降的，因此，储能充电站是未来趋势。我们当前应该以盈利为目标，精细化设计、建设、运营储能充电站，而不是不考虑成本的示范性储能场站。只有真正的积累了数据、经验、人才，才能更合理的去规划、建设储能充电站项目；只有找到了自己的赢利平衡点，才能知道何时大规模推广、占领市场。