一、RRT算法原理及实现效果

关于RRT算法的原理，博主之前看到的RRT算法原理图解这篇文章讲的很好，通俗易懂，所以若不了解RRT算法的原理，推荐各位看这个了解下。

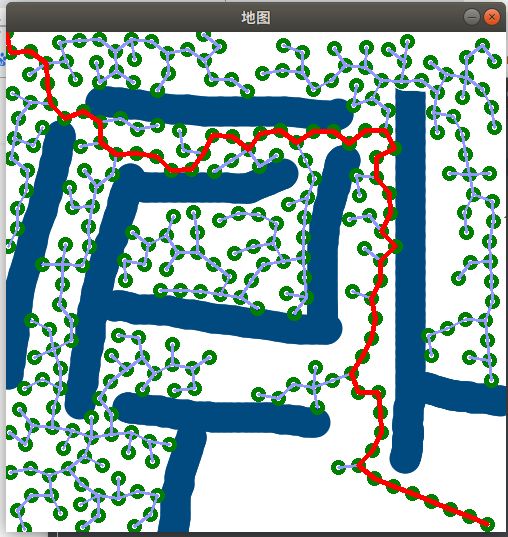
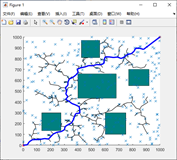
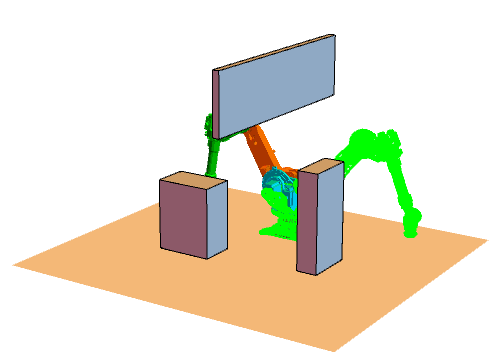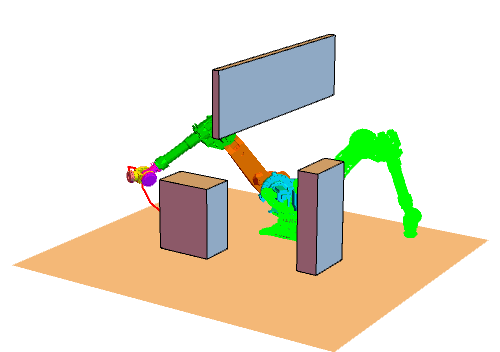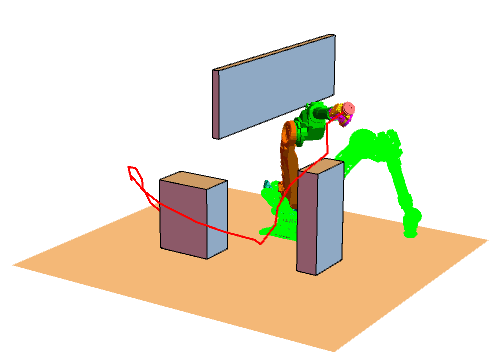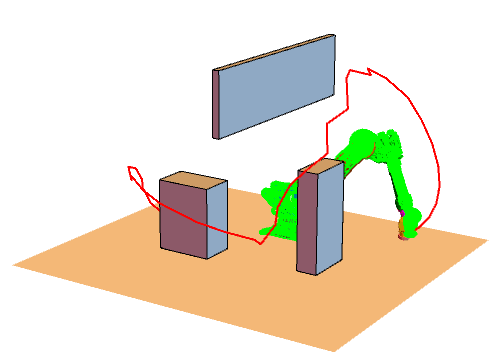
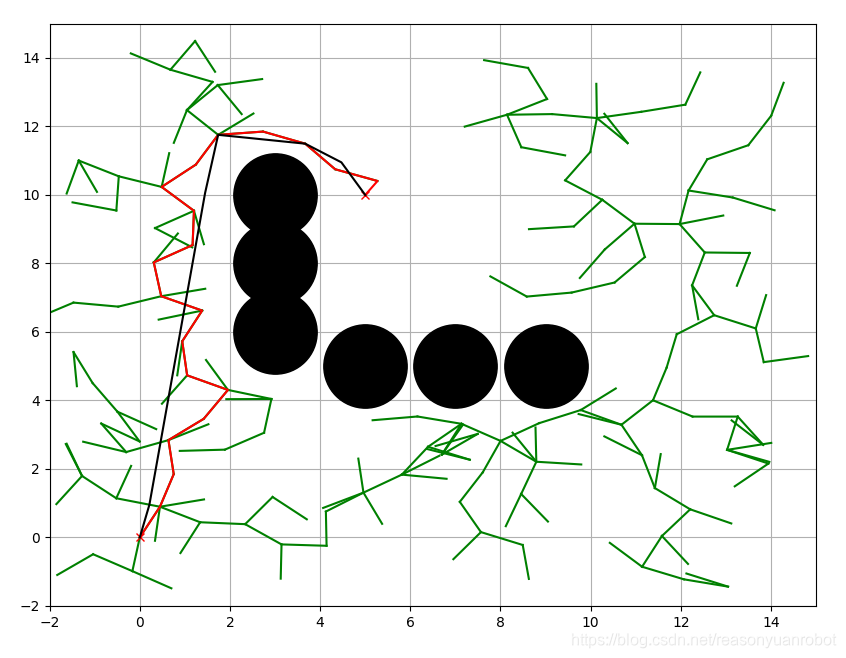
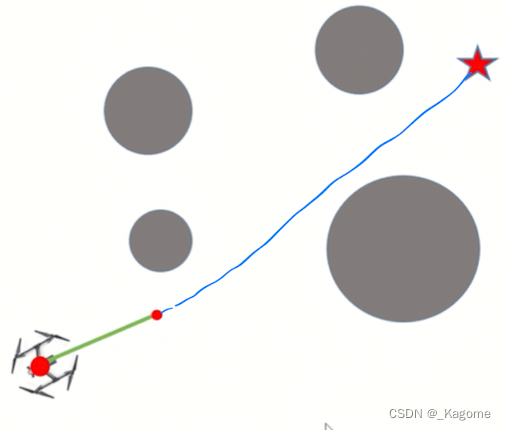
本文主要是基于Python实现RRT算法，先来看一下RRT算法实现后的效果图。
在这里插入图片描述

图1 RRT算法的实现效果图

二、RRT算法python代码实现

具体实现代码如下，博主写的可能有些复杂，不过其中大部分代码注释的很详细了，在这里我就不在赘述了。

import matplotlib.pyplot as plt
import random
import math
import timedef main():starttime = time.time()#    程序运行时间计时开始region1 = region(100,100)#    定义单元区域obstacle_area1 = obstacle_area((50,0),(50,80),(60,0),(60,80))#    定义障碍物区域tree_point = []  #    存放起点、终点和所有的可用衍生点futher = {}  #     存放所有可用衍生点的父节点step = 3#    步进系数breed_point = 'breed_point is invalid'draw_tree_pointx = []#    存放可用衍生点的横坐标draw_tree_pointy = []#    存放可用衍生点的纵坐标draw_plan_pointx = []#    存放从起点到终点的计划路径点的横坐标draw_plan_pointy = []#    存放从起点到终点的计划路径点的纵坐标initial_point = point()#    实例化起点对象initial_point.set_position(10,10)#    设定起点坐标initial_point.set_state(in_obstacle_area(initial_point,obstacle_area1,region1))#    设定起点状态if initial_point.state == False:#    若起点在障碍物区域，直接退出print("initial point is live in obstacle region , please choose initial point again")returnterminal_point = point()#    实例化终点对象terminal_point.set_position(90,50)#    设定终点坐标terminal_point.set_state(in_obstacle_area(terminal_point,obstacle_area1,region1))#    设定终点状态if terminal_point.state == False:#    若终点在障碍物区域，直接退出print("terminal point is live in obstacle region , please choose terminal point again")returntree_point.append([initial_point.x, initial_point.y])#   把起点加入tree_point集合列表中while (breed_point == 'breed_point is invalid') or (math.sqrt((tree_point[-1][0] - terminal_point.x) ** 2 + (tree_point[-1][1] - terminal_point.y) ** 2) > 3):radom_point = random_num(region1,obstacle_area1)#   生成有效随机点min_point = MinPoint(tree_point, radom_point)#   从tree_point合集列表中选取距离有效随机点最近的点breed_point = BreedPoint(min_point, radom_point, step, obstacle_area1,region1)#   在距离有效随机点最近的点的基础上选取有效的衍生点if breed_point != 'breed_point is invalid':futher[tuple(breed_point.get_position())] = tuple(breed_point.get_futher())#    记录有效衍生点的父节点tree_point.append([breed_point.x, breed_point.y])#    将有效衍生点加入到衍生点集合列表draw_tree_pointx.append(tree_point[-1][0])#    记录可用衍生点的横坐标draw_tree_pointy.append(tree_point[-1][1])#    记录可用衍生点的纵坐标futher[tuple(terminal_point.get_position())] = tuple(tree_point[-1])#    将终点的父节点设置为最后加入的tree_point点tree_point.append([terminal_point.x, terminal_point.y])#    把终点加入tree_point集合列表中current_cheak_point = tuple(terminal_point.get_position())while futher[current_cheak_point] != tuple(initial_point.get_position()):#    从终点开始往回寻找父节点，直到找到起点为止draw_plan_pointx.append(current_cheak_point[0])#    记录从起点到终点的计划路径点的横坐标draw_plan_pointy.append(current_cheak_point[1])#    记录从起点到终点的计划路径点的纵坐标current_cheak_point = futher[current_cheak_point]draw_plan_pointx.append(current_cheak_point[0])  # 记录父节点为起点的点的横坐标draw_plan_pointx.append(initial_point.x)#    记录起点的横坐标draw_plan_pointy.append(current_cheak_point[1])  # 记录父节点为终点的点的横坐标draw_plan_pointy.append(initial_point.y)#    记录终点的横坐标plt.scatter(draw_tree_pointx, draw_tree_pointy, c='green', s=3)#    画出所有的可用衍生点plt.plot([obstacle_area1.obstacle_point1[0],obstacle_area1.obstacle_point2[0],obstacle_area1.obstacle_point4[0],obstacle_area1.obstacle_point3[0],obstacle_area1.obstacle_point1[0]],[obstacle_area1.obstacle_point1[1],obstacle_area1.obstacle_point2[1],obstacle_area1.obstacle_point4[1],obstacle_area1.obstacle_point3[1],obstacle_area1.obstacle_point1[1]],color='r', markerfacecolor='blue', marker='o')#    画处障碍物区域plt.plot(draw_plan_pointx, draw_plan_pointy, color='r', markerfacecolor='blue', marker='o')#    画出从起点到终点的计划路径点plt.axis("equal")plt.grid(True)plt.title('initial_point' + str(initial_point.get_position()) + ' , terminal_point:' + str(terminal_point.get_position()))plt.show()endtime = time.time()#    程序运行时间计时结束dtime = endtime - starttime#    计算程序运行时长print("程序运行时间：%.8s s" % dtime)  #    显示到微秒def BreedPoint(min_point, radom_point, step,obstacle_area,region):#    在距离有效随机点最近的点的基础上选取有效的衍生点New_BreedPoint = point()#    实例化衍生点对象if (min_point[0] == radom_point.x):#    若有效随机点和距离其最近的点的横坐标一样New_BreedPoint.set_position(min_point[0], step + min_point[1])else:k = (min_point[1] - radom_point.y) / (min_point[0] - radom_point.x)#    计算有效随机点和距离其最近的点之间的斜率New_BreedPoint_x = math.cos(math.atan(k)) * step + min_point[0]New_BreedPoint_y = math.sin(math.atan(k)) * step + min_point[1]New_BreedPoint.set_position(New_BreedPoint_x, New_BreedPoint_y)if in_obstacle_area(New_BreedPoint, obstacle_area,region) is False:#   判断点是否在有效区域内return 'breed_point is invalid'New_BreedPoint.set_futher(min_point)#   设置衍生点的父节点return New_BreedPointdef random_num(region,obstacle_area):#   生成有效随机点radom_point = point()#    实例化随机点对象radom_point.set_position(random.randint(0, region.length), random.randint(0, region.width))#   生成随机点坐标if in_obstacle_area(radom_point, obstacle_area,region) is False:#   判断随机点是否在无效区域内random_num(region,obstacle_area)#   重新生成随机节点return radom_pointdef in_obstacle_area(check_point,obstacle_area,region):#   判断点是否在有效区域内if ((check_point.x >= obstacle_area.obstacle_point1[0]) and (check_point.x <= obstacle_area.obstacle_point3[0]) and (check_point.y <= obstacle_area.obstacle_point2[1]) and (check_point.y >= obstacle_area.obstacle_point1[1])) :#   判断点是否在障碍物区域内return Falseelif ((check_point.x >= 0) and (check_point.x <= region.length) and (check_point.y >= 0) and (check_point.y <= region.width)):#   判断点是否在单元区域内return Trueelse:return Falsedef MinPoint(tree_point, radom_point):#   从tree_point合集列表中选取距离有效随机点最近的点Distance = []for i in range(0, len(tree_point)):Distance.append(math.sqrt((tree_point[i][0] - radom_point.x) ** 2 + (tree_point[i][1] - radom_point.y) ** 2))return tree_point[Distance.index(min(Distance))]class point():def set_position(self, x, y):self.x = xself.y = ydef set_state(self, state):self.state = statedef set_futher(self, futher):self.futher = futherdef get_position(self):return [self.x, self.y]def get_state(self):return self.statedef get_futher(self):return self.futherclass region():def __init__(self,length,width):self.length = lengthself.width = widthclass obstacle_area():def __init__(self,obstacle_point1,obstacle_point2,obstacle_point3,obstacle_point4):self.obstacle_point1 = obstacle_point1#   左下点self.obstacle_point2 = obstacle_point2#   左上点self.obstacle_point3 = obstacle_point3#   右下点self.obstacle_point4 = obstacle_point4#   右上点if __name__ == '__main__':main()