概率图模型(PGM),作为机器学习的重要分支,能串连起很多传统模型,比如 NB、LR、MEM、HMM、CRF、DBN 等。本篇文章,从串连多个模型的角度,来谈谈 PGM,顺便把这些模型回顾下。
1 Why PGM
从两方面谈谈学习和使用 PGM 的必要性吧。
1.1 关系型数据
关系型数据具备下述两个特性:
- 细粒度数据本身,提供了部分特征,可以用于细粒度数据的分类
- 细粒度数据之间,存在的概率依赖关系,可以辅助(甚至是关键要素)细粒度数据的分类
例如:
- NLP 中的 POS、NER 任务,针对细粒度数据——字符——直接分类显然不合理,考虑字符间的依赖关系,通常将细粒度数据组合为粗粒度数据——语句,然后用模型来捕捉细粒度数据之间的依赖关系
- 图像处理中的边缘检测任务,为利用细粒度数据——像素——之间的相邻信息,通常基于粗粒度数据——图像——进行建模
- 网页分类任务中,除了网页内文本可以提供特征外,网页间的超链接关系也可以提供分类表现
现在,处理关系型数据,大家可能都习惯了使用自动化的 DL 模型,诸如 CNN 利用划窗累积的方式 model 数据间的关系。
而,PGM 提供了一种不是那么自动化的,处理关系型数据的强大框架。
1.2 概率模型
很多大牛推崇机器学习的概率论视角,比如 Murphy 那本 MLAPP、Uber 的 Zoubin Ghahramani 等。当然,概率模型和非概率模型之间的界限并不是泾渭分明的,例如,SVM、KNN、Ensemble 类模型都属于非概率模型,NB、HMM 属于概率模型,但决策树、LR、MEM、CRF 既可以看做非概率模型也可以看做概率模型。
PGM 用图结构来可视化数据间的概率分布关系,提供了一种更直观精致的解释方式。
通常认为 DL 是 PGM 的一种实现方式,由于后者具备完善的理论基础,两者的结合也是目前研究的一个方向,早期的成果包括 DBN、DBM 等,其中主流方式就是利用 DL 做感知,PGM 做推断。
可见,深入浅出的了解下 PGM 还是很有必要的。
2 What is PGM
2.1 概率图模型
对于多元随机变量,在不做任何条件独立性假设情况下,其概率分布表示所需的参数是多元维度的指数级,往往难以接受。一种有效的方法就是引入变量之间的条件独立性假设。
PGM提供了一种直观的描述随机变量之间的条件独立性关系的视角,并且可以将多元随机变量的联合概率分布,分解为一些简单条件概率模型的组合,即 local func 的乘积形式,每个 local func 仅依赖于少量随机变量。
当然,这是对于一个非全连接图而言。
PGM,在形式上是由图结构组成的。图的每个节点 node 都关联了一个随机变量,图的边 edge 则用于编码这些随机变量之间的关系。
图上随机变量的依赖关系可以是单向的也可以是双向的,从而可以将 PGM 分类为有向无环图模型(即贝叶斯网络),无向图模型(即马尔科夫网络)。
具体介绍之前,引入几个基本概念:
- X X X 为输入变量集合, Y Y Y 为输出变量集合, V = X ∪ Y V=X \cup Y V=X∪Y 为所有随机变量集合,共 K K K 个, V k ∈ V V_k \in V Vk∈V 为其中一个随机变量, v v v 为 V V V 的一个取值, v k v_k vk 为 V k V_k Vk 的一个取值
- 图表示为 G = ( V , E ) G=(V,E) G=(V,E) ,其中, E E E 为边的集合,边在有向图中表示两个变量之间的因果关系
- 有向图中, π ( V k ) \pi(V_k) π(Vk) 为变量 V k V_k Vk 在图中所有的父节点构成的变量集合
- 无向图中, C C C 表示图中的一个最大团, V C V_C VC 表示其对应的随机变量集合,其一个取值为 v C ∈ V C v_C \in V_C vC∈VC
2.2 有向图模型(贝叶斯网络)
有向图中,依赖关系仅存在于父子节点之间,概率分布可分解为:
p ( v ) = ∏ k = 1 K p ( v k ∣ π ( v k ) ) p(v)=\prod_{k=1}^{K}{p(v_k \mid \pi(v_k))} p(v)=k=1∏Kp(vk∣π(vk))
无向图模型(马尔科夫网络)
定义:如果联合概率分布 P ( V ) P(V) P(V) 满足成对、局部或全局马尔可夫性,就称此联合概率分布为概率无向图模型或马尔可夫随机场(网络)。
无向图中,依赖关系通常基于全连通子图来分割,利用 H-C 定理给出概率分解形式为:
p ( v ) = 1 Z ∏ C ψ C ( v C ) p(v)= \frac{1}{Z} \prod_C{\psi_C(v_C)} p(v)=Z1C∏ψC(vC)
其中,partition func Z = ∑ v ∏ C ψ C ( v C ) Z=\sum_v{\prod_C{\psi_C(v_C)}} Z=∑v∏CψC(vC) 为归一化因子,保证概率和为1,potential func ψ C \psi_C ψC 为定义在最大团 C C C 上的严格正函数。
- potential func 通常定义为 ψ C ( v C ∣ ω C ) = e x p ( ω C f C ( v C ) ) = e x p ∑ i ω i C f i C ( v C ) \psi_C(v_C \mid \omega_C)=exp(\omega_C f_C(v_C))=exp{\sum_i{\omega_{iC}} f_{iC}(v_C)} ψC(vC∣ωC)=exp(ωCfC(vC))=exp∑iωiCfiC(vC),其中, f C ( v C ) f_C(v_C) fC(vC) 为定义在 V C V_C VC 上的特征向量, ω C \omega_C ωC 为对应的权重向量, f i C f_{iC} fiC 为特征函数
- partition func 的计算复杂度是指数级的,大部分算法都是采用的近似计算
利用特征向量,无向图也可以表示为:
p ( v ) = 1 Z e x p ( ∑ C ω C f C ( v C ) ) p(v)= \frac{1}{Z} exp(\sum_C {\omega_Cf_C(v_C)}) p(v)=Z1exp(C∑ωCfC(vC))
2.3 联系
- 无向图可以表示有向图无法表示的一些依赖关系,比如循环依赖
- 有向图可以表示无向图无法表示的一些关系,比如因果关系
- 前面说的 local func,在有向图中为可解释的 p ( v k ∣ π ( v k ) ) p(v_k \mid \pi(v_k)) p(vk∣π(vk)),在无向图中为没有直接解释的 ψ C ( v C ) \psi_C(v_C) ψC(vC)
- 有向图通常用来建模生成模型,无向图通常用来建模判别模型,前者 p ( v ) p(v) p(v) 即为 p ( x , y ) p(x,y) p(x,y),后者通常为 p ( y ∣ x ) p(y \mid x) p(y∣x)
2.4 因子图模型
factor graph,是一个双向图,表示为 G = ( V , F , E ) G=(V,F,E) G=(V,F,E),其中, ψ C ∈ F \psi_C \in F ψC∈F 表示因子节点,如果变量节点 V k ∈ V V_k \in V Vk∈V 是 ψ C \psi_C ψC 的参数,则存在边 E i ∈ E E_i \in E Ei∈E 连接两者。
通常,无向图和有向图都可以更精确的表示为因子图模型。 具体后面会举例。
3. Examples
3.1 NB
NB 作为生成模型,先学习联合概率模型,然后利用贝叶斯公式进行分类:
p ( Y ∣ X ) = p ( X , Y ) p ( X ) = p ( Y ) p ( X ∣ Y ) ∑ Y p ( Y ) p ( X ∣ Y ) p(Y \mid X)=\frac{p(X,Y)}{p(X)}=\frac{p(Y)p(X|Y)}{\sum_Y{p(Y)p(X|Y)}} p(Y∣X)=p(X)p(X,Y)=∑Yp(Y)p(X∣Y)p(Y)p(X∣Y)
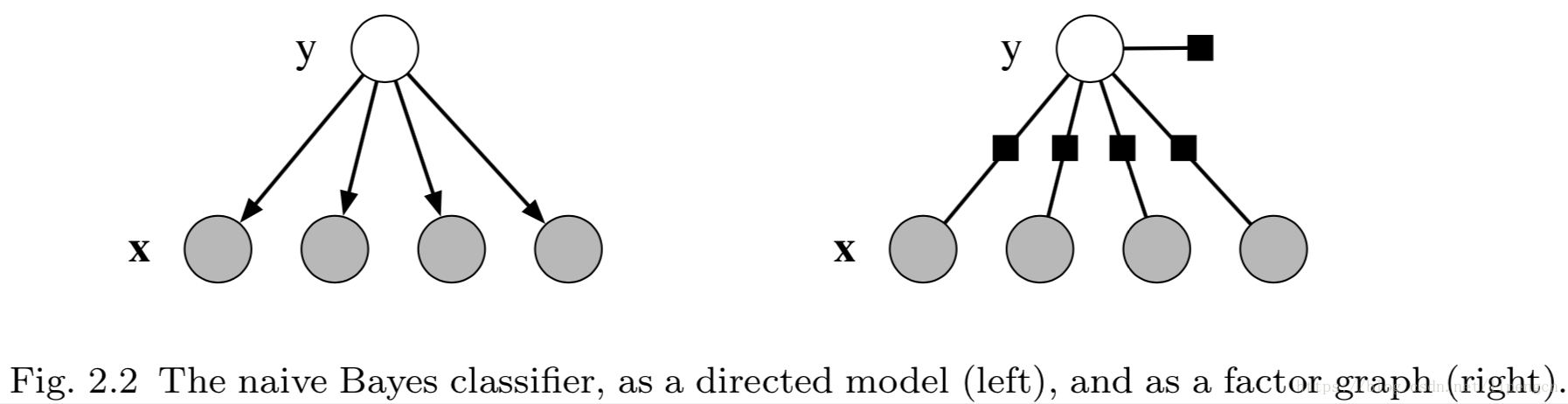
其中,联合概率分布形式为 p ( x , y ) = p ( y ) ∏ i p ( x i ∣ y ) p(x,y)=p(y)\prod_i{p(x_i \mid y)} p(x,y)=p(y)∏ip(xi∣y),可以对应到有向图模型,如下图左图所示。
同时,如果定义一个因子 ψ ( y ) = p ( y ) \psi(y)=p(y) ψ(y)=p(y),针对每个特征 x i x_i xi 定义一个因子 ψ k ( y , x i ) = p ( x i ∣ y ) \psi_k(y,x_i)=p(x_i \mid y) ψk(y,xi)=p(xi∣y),就可以表示为因子图模型了,如下图右图所示。
3.2 LR
LR 作为判别模型,不必去学联合概率分布。LR 可以理解为每个 class 的对数概率,即 l o g p ( y ∣ x ) log{p(y|x)} logp(y∣x),是特征向量 x x x 的线性函数,也可以理解为条件概率分布的形式为参数化的逻辑斯蒂分布的概率模型,形式都为:
p ( y ∣ x ) = 1 Z ( x ) e x p ( ∑ i ω y i x i ) p(y \mid x) = \frac{1}{Z(x)}{exp(\sum_i{\omega_{{y}i}x_i})} p(y∣x)=Z(x)1exp(i∑ωyixi)
引入特征函数 f y ′ i ( y , x ) = 1 ( y ′ = y ) x i f_{y'i}(y,x)=1(y'=y)x_i fy′i(y,x)=1(y′=y)xi,可以将所有 class 的权重向量合并为一个向量。用 f k f_k fk 来表示 f y ′ i f_{y'i} fy′i, 相应权重表示为 ω k \omega_k ωk,可以将 LR 模型重新写作:
p ( y ∣ x ) = 1 Z ( x ) e x p ( ∑ k ω k f k ( y , x ) ) p(y \mid x) = \frac{1}{Z(x)}{exp(\sum_k{\omega_k f_k(y,x)})} p(y∣x)=Z(x)1exp(k∑ωkfk(y,x))
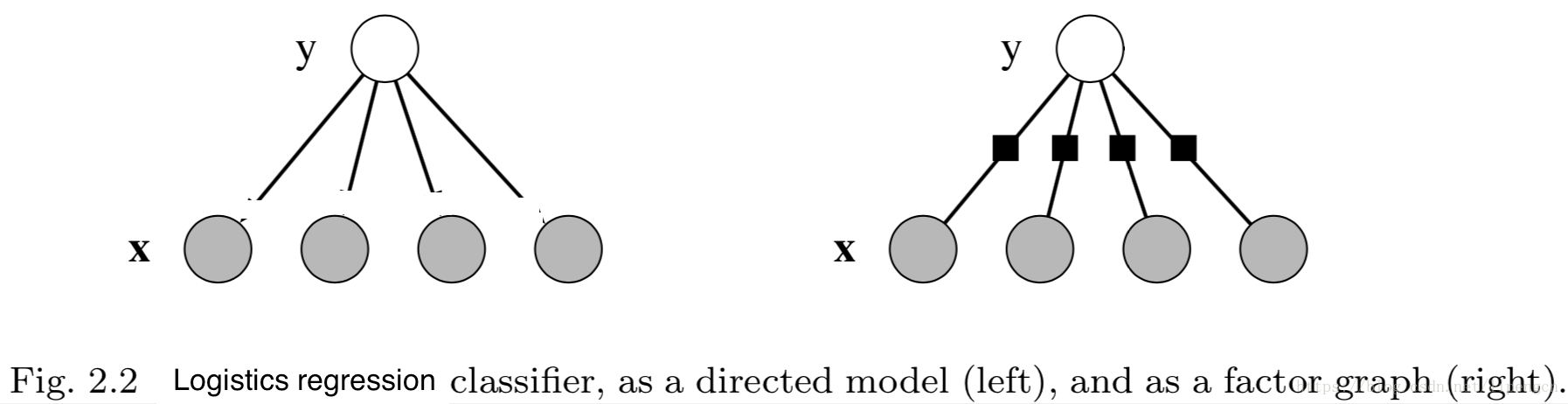
可以看出,LR 相当于“以 ( y , x i ) (y,x_i) (y,xi)为最大团”的无向图,结构图如下:
可以看出,NB 和 LR 是由相似的图拓扑分别衍生的生成模型和判别模型
3.3 MEM
最大熵模型算是 LR 的通用形式,定义 f i ( x , y ) f_i(x,y) fi(x,y) 为特征函数,形式为
p ( y ∣ x ) = 1 Z ( x ) e x p ( ∑ i ω i f i ( x , y ) ) p(y \mid x) = \frac{1}{Z(x)}{exp(\sum_i{\omega_i f_i(x,y)})} p(y∣x)=Z(x)1exp(i∑ωifi(x,y))
当变量 y y y 二项分布,且特征函数仅有两个 f 1 ( x , y ) = x f_1(x,y)=x f1(x,y)=x, f x ( x , y ) = x y f_x(x,y)=xy fx(x,y)=xy时,MEM 等价于 LR。
当然还有一个扩展维度是,LR 的变量 y y y 扩展为多项式分布,但特征函数不变,则成了 softmax 回归。
3.4 HMM
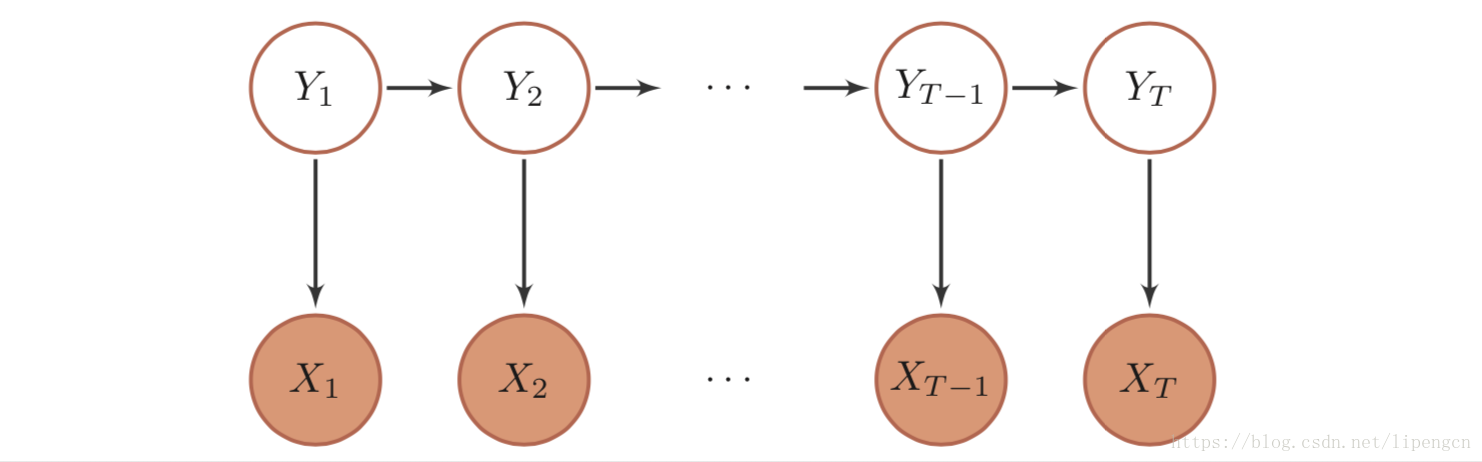
HMM 作为生成模型,模型 λ = ( π , A , B ) \lambda=(\pi,A,B) λ=(π,A,B) 的联合概率可以写作:
p ( x , y ) = ∏ t = 1 T p ( y t ∣ y t − 1 ) p ( x t ∣ y t ) p(x,y)=\prod_{t=1}^T {p(y_t \mid y_{t-1}) p(x_t \mid y_t)} p(x,y)=t=1∏Tp(yt∣yt−1)p(xt∣yt)
很容易看出来,HMM 即满足“输出(状态)满足齐次马尔科夫性假设,输入(观测)满足独立性假设”的有向图模型。图拓扑如下:
3.5 MEMM
3.6 CRF
CRF 作为判别模型,其条件概率形式同 MEM,但 y y y 为随机向量,形式为:
p ( y ∣ x ) = 1 Z ( x ) e x p ( ∑ C ω C f C ( x , y C ) ) p(y \mid x) = \frac{1}{Z(x)}{exp(\sum_C{\omega_C f_C(x,y_C)})} p(y∣x)=Z(x)1exp(C∑ωCfC(x,yC))
可见,CRF 中最大团的概念只针对 y y y 不包含 x x x,对应 CRF 的定义 “条件概率满足马尔科夫随机场”。
常用的还是线性链 CRF,形式为:
p ( y ∣ x , ω ) = 1 Z e x p ( ∑ m ∑ t = 1 T ω 1 m f 1 m ( x , y t ) + ∑ n ∑ t = 1 T − 1 ω 2 n f 2 n ( x , y t , y t + 1 ) ) p(y \mid x, \omega) = \frac{1}{Z} exp(\sum_m\sum_{t=1}^T \omega_{1m} f_{1m}(x,y_t) + \sum_n\sum_{t=1}^{T-1} \omega_{2n} f_{2n}(x,y_t,y_{t+1})) p(y∣x,ω)=Z1exp(m∑t=1∑Tω1mf1m(x,yt)+n∑t=1∑T−1ω2nf2n(x,yt,yt+1))
= 1 Z e x p ( ∑ t = 1 T ω 1 f 1 ( x , y t ) + ∑ t = 1 T − 1 ω 2 f 2 ( x , y t , y t + 1 ) ) = \frac{1}{Z} exp(\sum_{t=1}^T {\omega_1f_1(x,y_t)} + \sum_{t=1}^{T-1} {\omega_2f_2(x,y_t,y_{t+1})}) =Z1exp(t=1∑Tω1f1(x,yt)+t=1∑T−1ω2f2(x,yt,yt+1))
= 1 Z e x p ( ω 1 f 1 ( x , y ) + ω 2 f 2 ( x , y ) ) = \frac{1}{Z} exp({\omega_1 f_1(x,y) + \omega_2 f_2(x,y)}) =Z1exp(ω1f1(x,y)+ω2f2(x,y))
= 1 Z e x p ( ω f ( x , y ) ) = \frac{1}{Z} exp(\omega f(x,y)) =Z1exp(ωf(x,y))
= 1 Z e x p ( ∑ k = 1 K ω k f k ( x , y ) ) = \frac{1}{Z} exp({\sum_{k=1}^K \omega_k f_k(x,y)}) =Z1exp(k=1∑Kωkfk(x,y))
其中, f 1 f_1 f1 为状态特征向量, f 2 f_2 f2 为转移特征向量, f f f 为全局特征向量, f k f_k fk 第 k k k类特征值在 T T T个位置的和。
3.7 对比
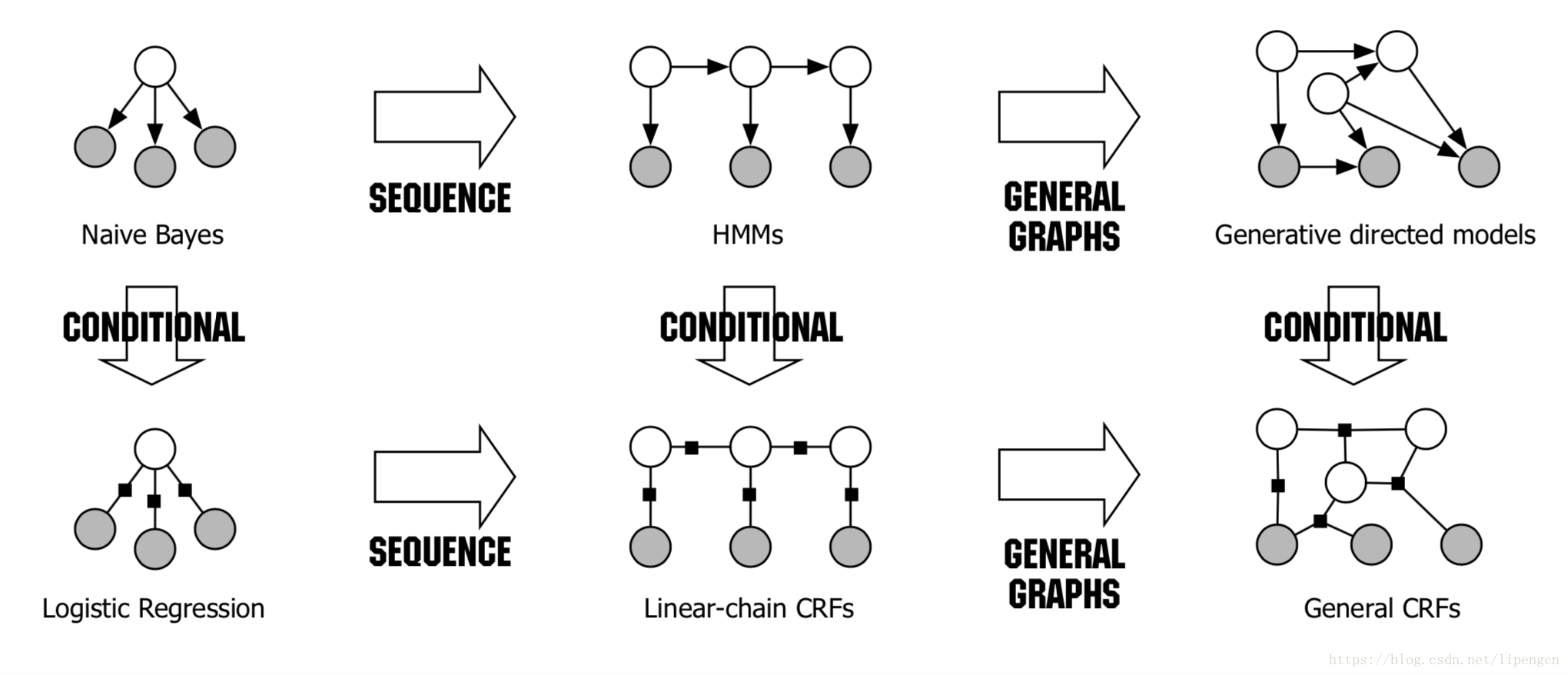
下图展示了前面介绍到的几个经典模型的对比,可以从多个角度来理解,一个是纵向的“生成模型-判别模型”角度,一个是横向的推广过程。
其中,白色为 Y,或称状态 I,灰色为 X,或称观测 O。
生成模型-判别模型
判别模型不去 model 对分类没用的 p ( x ) p(x) p(x),这是因为 model p ( x ) p(x) p(x) 需要考虑很多高度依赖的特征;例如 HMM 处理 NER 时由于 HMM 仅依赖于词的实体这一个特征,而在训练数据中可能很多人名从未出现过,可见 entity-word 特征包含信息量有限。
而判别模型的主要优点就是可以便于包含丰富的重叠的各种特征。
当然,生成模型也有优点:
- 能自然的处理潜变量、部分标注数据、无标注数据,如 HMM 中的无监督学习方式——BW 算法
- 当数据集比较小时,生成模型比判别模型可能表现更好,可能是由于 p ( x ) p(x) p(x) 对条件概率的平滑作用
类似于NB 和 LR 构成了“生成模型-判别模型”对,HMM 和 CRF 也构成了“生成模型-判别模型”对,即上图的纵向对比。
HMM v.s. CRF
(1)HMM
- 模型 p ( X , Y ) p(X,Y) p(X,Y) - λ \lambda λ ,状态 Y Y Y - I I I,观测 X X X - O O O
- 评估,给定 λ \lambda λ 和 O O O,计算 p ( O ∣ λ ) p(O | \lambda) p(O∣λ),前向后向算法
- 有监督学习,给定 O O O 和 I I I,计算 p ( O , I ∣ λ ) p(O,I | \lambda) p(O,I∣λ) 最大的 λ \lambda λ,MLE
- 无监督学习,给定 O O O,计算 p ( O ∣ λ ) p(O|\lambda) p(O∣λ) 最大的 λ \lambda λ,B-W算法
- 预测,给定 λ \lambda λ 和 O O O,计算 p ( I ∣ O , λ ) p(I|O,\lambda) p(I∣O,λ) 最大的 I I I,Viterbi算法
(2)CRF
- 模型 p ( Y ∣ X ) p(Y|X) p(Y∣X) - λ \lambda λ,状态 Y Y Y - I I I,观测 X X X - O O O
- 评估,给定 λ \lambda λ 和 I I I、 O O O,计算 p ( i t ∣ O , λ ) p(i_t|O,\lambda) p(it∣O,λ) 和 p ( i t − 1 , i t ∣ O , λ ) p(i_{t-1},i_t|O,\lambda) p(it−1,it∣O,λ),前向后向算法
- 有监督学习,给定 O O O 和 I I I,计算 p ( O , I ∣ λ ) p(O,I | \lambda) p(O,I∣λ) 最大的 λ \lambda λ,MLE
- 预测,给定 λ \lambda λ 和 O O O,计算 p ( I ∣ O , λ ) p(I|O,\lambda) p(I∣O,λ) 最大的 I I I,Viterbi算法
4、其他
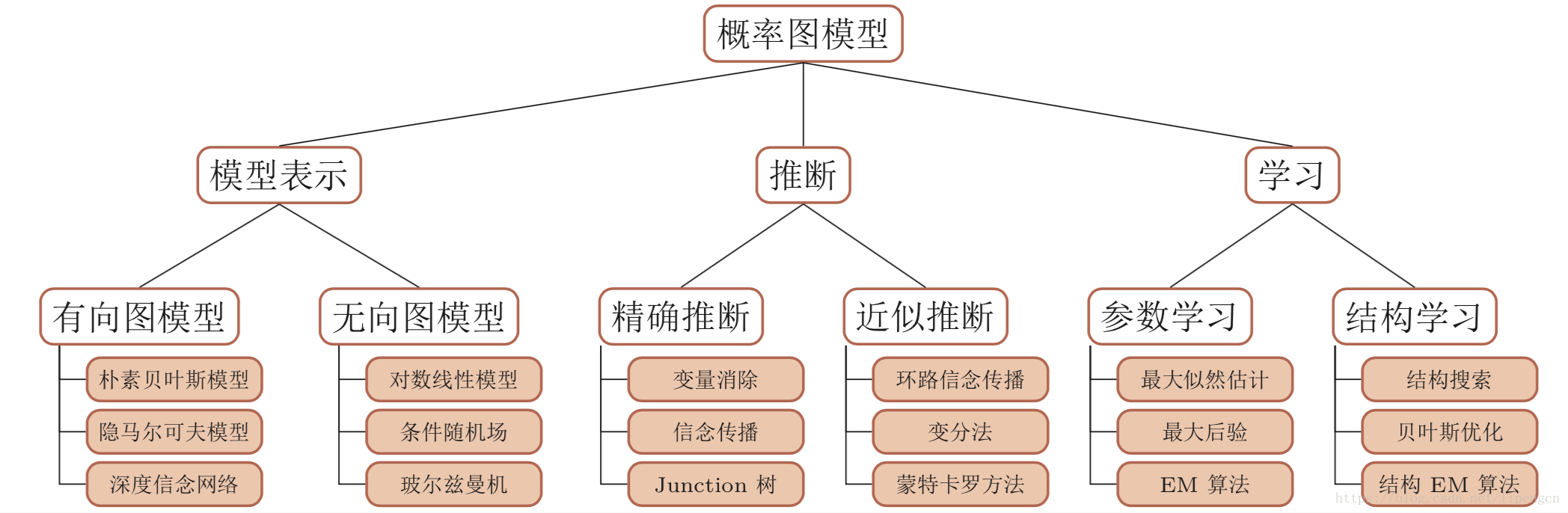
当然,上面只是介绍了 PGM 的一部分,其所蕴含的内容还有很多,体系如下,有空再聊吧。
CRF 应用
这里额外补充一下 CRF 在序列标注问题上的应用。以 POS 为例:
(1)特征构造
- s1(yi,x,i)=1 ,如果 yi=ADVERB 且 xi 以“-ly”结尾;否则为 0 。
- s2(yi,x,i)=1,如果 i=1 、yi=VERB 且 x 以“?”结尾;否则为 0 。
- t3(yi−1,yi,x,i)=1,如果 yi−1=ADJECTIVE 且 yi=NOUN;否则为 0 。
- t4(yi−1,yi,x,i)=1,如果 yi−1=PREPOSITION 且 yi=PREPOSITION;否则为 0 。
可见,CRF 相对 HMM 能 model 到全局 x 信息,且模型参数没有 HMM 中的限制。
(2)CRF++
训练数据、测试数据
下例中tokenizer为标签,pos做额外转移信息:
He PRP B-NP
reckons VBZ B-VP
the DT B-NP
current JJ I-NP
account NN I-NP
deficit NN I-NP
will MD B-VP
narrow VB I-VP
to TO B-PP
only RB B-NP
# # I-NP
1.8 CD I-NP
billion CD I-NP
in IN B-PP
September NNP B-NP
. . OHe PRP B-NP
reckons VBZ B-VP
..
特征模板
Input: Data
He PRP B-NP
reckons VBZ B-VP
the DT B-NP << CURRENT TOKEN
current JJ I-NP
account NN I-NPtemplate expanded feature
%x[0,0] the
%x[0,1] DT
%x[-1,0] reckons
%x[-2,1] PRP
%x[0,0]/%x[0,1] the/DT
ABC%x[0,1]123 ABCDT123
可见,可以利用%x[0,t]中的t控制采用状态特征还是转移特征。
以这样的标准宏将想要的特征写到特征模板文件中,CRF++将自动去提取特征。
(3)biLSTM-CNN-CRF
将”词向量“与”词的基于字符的CNN表征“拼接后,接入biLSTM,隐状态拼接后,当做观测 X 输入CRF,利用 CRF 预测 状态。
5、references
[1] Charles Sutton, An Introduction to Conditional Random Fields.
[2] 邱锡鹏, 神经网络与深度学习.
[3] https://www.cnblogs.com/Determined22/p/6750327.html
[4] https://www.cnblogs.com/Determined22/p/6915730.html