Logistic Regression（逻辑回归）

分类算法是典型的监督学习，分类算法通过对训练样本的学习，得到从样本特征到样本的标签之间的映射关系，也被称为假设函数，之后可利用该假设函数对新数据进行分类。

通过训练数据中的正负样本，学习样本特征到样本标签之间的假设函数，Logistic Regression算法是典型的线性分类器，有算法复杂度低、容易实现等特点。

Logistic Regression模型

线性可分和线性不可分

对于一个分类问题，通常可以分为线性可分与线性不可分两种。如果一个分类问题可以使用线性判别函数正确分类，则称该问题为线性可分否则为线性不可分问题

Logistic Regression模型

对于图1.1 所示的线性可分的问题，需要找到一条直线，能够将两个不同的类区分开，这条直线也称为超平面。 在Logistic Regression算法中，通过对训练样本的学习，最终得到该超平面，将数据分成正负两个类别如图1.1所示，

对于上述的超平面，可以使用如下的线性函数表示：
$$Wx+b=0$$
（W为权重，b为偏置，若在多维的情况下，权重W 和偏置b均为向量）

可以使用阈值函数，将样本映射到不同的类别中，常见的阈值函数有Sigmoid函数，其形式如下所示：
$$f(x)=\frac{1}{1+e^{-x}}$$
Sigmoid函数的图像

从Sigmoid函数的图像可以看出，其函数的值域为（0，1），在0附近的变化比较明显。其导函数 f′（x）为：

Python实现Sigmoid函数

import numpy as np
def sig(x):'''Sigmoid函数input: x(mat):feature*Woutput: sigmoid(x)(mat):Sigmoid值'''return 1.0/(1+np.exp(-x))

Sigmoid函数的输出为sigmoid值，对于输入向量X，其属于正例的概率为：

σ 表示的是Sigmoid函数。那么，对于输入向量X，其属于负例的概率为：

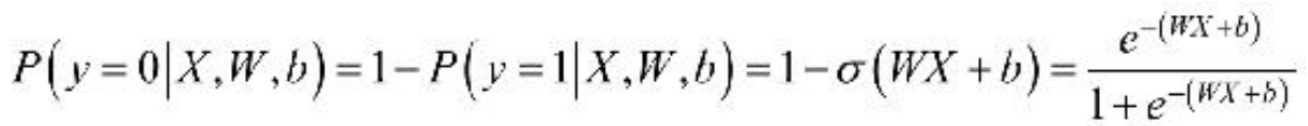
对于Logistic Regression算法来说，需要求解的分隔超平面中的参数，即为权重矩阵W 和偏置向量b，那么，这些参数该如何求解呢？为了求解模型的两个参数，首先必须定义损失函数。

损失函数

对于上述的Logistic Regression算法，其属于类别y的概率为：

要求上述问题中的参数W 和b，可以使用极大似然法对其进行估计。假设训练数据集有m个训练样本{（X（1），y（1）），（X（2），y（2）），…，（X（m） ，y（m））}，则其似然函数为：

其中，假设函数为：

对于似然函数的极大值的求解，通常使用Log似然函数，在Logistic Regression算法中，通常是将负的Log似然函数作为其损失函数，即the negativelog-likelihood （NLL）作为其损失函数，此时，需要计算的是NLL的极小值。损失函数lW，b 为：

为了求得损失函数lW，b 的最小值，可以使用基于梯度的方法进行求解。

梯度下降法

在机器学习算法中，对于很多监督学习模型，需要对原始的模型构建损失函数l，接下来便是通过优化算法对损失函数l进行优化，以便寻找到最优的参数W。在求解机器学习参数W 的优化算法时，使用较多的是基于梯度下降的优化算法（Gradient Descent，GD）。

优点：求解过程中只需求解损失函数的一阶导数，计算成本较小，能在很多大规模数据集上得到应用

含义：通过当前点的梯度方向寻找到新的迭代点，并从当前点移动到新的迭代点继续寻找新的迭代点，直到找到最优解。

梯度下降法的流程

根据初始点在每一次迭代的过程中选择下降法方向，进而改变需要修改的参数，对于优化问题min f（w），梯度下降法的详细过程如下所示。

• 随机选择一个初始点W₀
• 重复以下过程

• 决定梯度下降的方向
• 选择步长a
• 更新：W_i+1=W_i+a·d_i
• 直到满足终止条件

具体过程如图1.4所示

在初始时，在点w₀ 处，选择下降的方向d₀ ，选择步长α ，更新w的值，此时到达w₁ 处，判断是否满足终止的条件，发现并未到达最优解w^∗ ，重复上述的过程，直至到达w^∗。

凸优化与非凸优化

凸优化问题是指只存在一个最优解的优化问题，即任何一个局部最优解即全局最优解，如图1.5所示。

非凸优化是指在解空间中存在多个局部最优解，而全局最优解是其中的某一个局部最优解，如图1.6所示。

最小二乘（Least Squares）、岭回归（Ridge Regression）和Logistic回归（Logistic Regression）的损失函数都是凸优化问题。

利用梯度下降法训练Logistic Regression模型

对于上述的Logistic Regression算法的损失函数可以通过梯度下降法对其进行求解，其梯度为：