枚举算法

article/2025/8/23 14:48:47

一、枚举法的基本思想

枚举法又称穷举法。

基本思想是根据提出的问题枚举所有可能状态，并用问题给定的约束条件检验哪些状态是需要的，哪些状态是不需要的。

能使命题成立的状态，即为其解。

枚举结构：循环+判断语句。

二、枚举法的条件

适合于枚举法求解的问题必须满足以下两个条件：

⑴可预先确定每个状态的元素个数n。

如百钱买百鸡，状态元素可预先确定。

⑵状态元素a1，a2，…，an的可能值为一个连续的值域。

如果值域为实数级，每两个值之间有无穷个数，这就不能枚举出所有可能的值。

对于满足以上两个条件的问题，采用枚举法时，可以先确定枚举对象、枚举范围和判定条件，再一一枚举所有可能的解，验证是否是问题的解。

三、枚举法的框架结构

设ai1—状态元素ai的最小值；aik—状态元素ai的最大值(1≤i≤n)，即a11≤a1≤a1k，a21≤a2≤a2k， ai1≤ai≤aik， ……，an1≤an≤ank for(a1=a11;a1<=a1k;a1++)

for(a1=a11;a1<=a1k;a1++)for(a2=a21;a2<=a2k;a2++).....for(ai=ai1;ai<=aik;ai++).....for(an=an1;an<=ank;an++)if(状态(a1,...,ai...,an)满足检验条件)输出问题的解;

  例题1：数字统计(2010普及)

请统计某个给定范围[L, R]的所有整数中，数字 2 出现的次数。

比如给定范围[2, 22]，数字 2 在数 2 中出现了 1 次，在数 12 中出现 1 次，在数 20 中出现 1 次，在数 21 中出现 1 次，在数 22 中出现 2 次，所以数字 2 在该范围内一共出现了 6次。

输入输出格式

输入格式：

输入共 1 行，为两个正整数 L 和 R，之间用一个空格隔开。

输出格式：

输出共 1 行，表示数字 2 出现的次数。

输入输出样例

【输入样例1】 2 22 【输入样例2】 2 100

【输出样例1】 6 【输出样例2】 20

cin>>m>>n;
ans=0;
for(i=m;i<=n;i++)//枚举n-m+1个状态
{    k=i;while(k)//{    if(k%10==2)ans++;k=k/10;}
}
cout<<ans<<endl;

例题2：砝码称重(NOIP1996)

【问题描述】设有1g、2g、3g、5g、10g、20g的砝码各若干枚（其总重<=1000），求用这些砝码能称出不同的重量的个数。 【输入】    

     输入1g、2g、3g、5g、10g、20g的砝码个数

【输出】  

     能称出不同的重量的个数

【输入样例】        

1 1 0 0 0 0

【输出样例】        

3

题目分析

根据输入的砝码信息，每种砝码可用的最大个数是确定的，而且每种砝码的个数是连续的，能取0到最大个数，所以符合枚举法的两个条件，可以使用枚举法。 枚举时，重量可以由1g,2g,……,20g砝码中的任何一个或者多个构成，枚举对象可以确定为6种重量的砝码，范围为每种砝码的个数。判定时，只需判断这次得到的重量是新得到的，还是前一次已经得到的，即判重。由于重量<=1000g，所以，可以开一个a[1005]的数组来判重，当得到x重量时，把a[x]置为1，下次再得到x时，还是置1，最后只需遍历一下a数组，即可得到重量的个数。算法实现时，伪代码如下：

memset(a,0,sizeof(a));  
cin>>a>>b>>c>>d>>e>>f;
for(c1=0;c1<=a;c1++) //1g砝码的个数for(c2=0;c2<=b;c2++) //2g砝码的个数for(c3=0;c3<=c;c3++) //3g砝码的个数for(c4=0;c4<=d;c4++) //5g砝码的个数for(c5=0;c5<=e;c5++) //10g砝码的个数for(c6=0;c6<=f;c6++) //20g砝码的个数{   sum=c1*1+c2*2+c3*3+c4*5+c5*10+c6*20;a[sum]=1; //标记}
for(i=1;i<=1000;i++)if(a[i])num++; //统计不同重量的个数
cout<<num<<endl;

例题3：防护伞

【题目简述】

平面上有n个点，现要以其中一个点为圆心画一个圆，使得这个圆能够覆盖所有的点，求最小圆的面积。

样例输入

3

0  1

-8  -4

-1  4

样例输出

279.6017

【注意】 精确到小数点后 4 位 π=3.1415926535

【数据范围】  

对于50%的数据：2 <= N <= 100  

对于100%的数据：2<=N<=1000，-10000<=x,y<=10000

题目分析：

依次枚举每一个点i，计算出点i与所有点j的距离dist[i,j]；

则以i为圆心覆盖所有点的圆的半径为：                  

R[i]=max{dist[i,j]|1<=j<=N}

因为要求圆的面积最小，即圆的半径最小，所以答案Ans=min{R[i]|1<=i<=N}。

【时间复杂度】O(N^2)

double x[1005],y[1005];
int main(){int i,j,n;double Max,Min=800000000,Pi=3.1415926535,dis;cin>>n;for(i=0;i<n;i++)cin>>x[i]>>y[i];for(i=0;i<n;i++){//枚举每一个点Max=0;for(j=0;j<n;j++) //找到这个点和其他点的最大距离if(i!=j){dis=(x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]);if(dis>Max)Max=dis;}if(Max<Min)Min=Max;//在所有的最大距离中找一个最小值}printf("%.4lf",Pi*Min);return 0;
}

四、枚举法的优缺点

枚举法的优点：

           比较直观，易于理解，其算法的正确性也比较容易证明。

枚举法的缺点：  

        当枚举的状态很多时，所用时间非常大，效率比较低。

 

五、枚举算法的优化

枚举算法的时间复杂度：状态总数*单个状态的耗时

主要优化方法：

      ⑴ 减少状态总数

      ⑵ 降低单个状态的考察代价

优化过程从以下几个方面考虑：

      ⑴ 枚举对象的选取

      ⑵ 枚举方法的确定

      ⑶ 采用局部枚举或引进其他算法

 

例题4：火柴棒等式（NOIP2008）

【问题描述】给你n根火柴棍，你可以拼出多少个形如“A+B=C”的等式？等式中的A、B、C是用火柴棍拼出的整数（若该数非零，则最高位不能是0）。用火柴棍拼数字0-9的拼法如图所示：

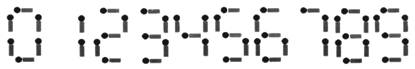
注意：

     1. 加号与等号各自需要两根火柴棍

     2. 如果A≠B，则A+B=C与B+A=C视为不同的等式（A、B、C≥0）

      3. n根火柴棍必须全部用上

【输入】输入文件仅一个整数n（n≤24）。

【输出】输出文件仅一行，表示能拼成的不同等式的数目。

题目分析

【问题简述】

  给你n(n<=24)根火柴棒,叫你拼出 “A+B=C”这样的等式,求方案数。

【思路点拨】

    本题主要考查对枚举法的掌握，可以枚举A和B的取值，考查等式是否刚好用了24根火柴棒。但是1S的时限对枚举的范围有所要求，必须要仔细分析A和B的取值。

n本题最多24根火柴，等号和加号共用4根火柴，所以A,B,C这3个数字需用20根火柴。我们考查A和B的最大的取值可能：0~9这10个数字所用的火柴数为6,2,5,5,4,5,6,3,7,6，很明显数字1用的火柴棒最少只要2根，不妨让B为1，那么A和C最多可以使用18根火柴，而C>=A，满足条件的A的最大取值为1111。所以枚举A和B的范围是从0~1111。

   cin>>n;n=n-4;for(i=0;i<=1111;i++)for(j=0;j<=1111;j++)if(c(i)+c(j)+c(i+j)==n)ans++;cout<<ans<<endl;

优化

为了加快速度，可以将0到2222的所有整数需要的火柴棒数目提前算好保存在数组中。

int n,a[2300]={6,2,5,5,4,5,6,3,7,6};//6,2本身不是连续数值，存入a数组后下标是连续的就可以用枚举int i,j,ans=0;cin>>n; n=n-4;for(i=10;i<=2222;i++)a[i]=a[i/10]+a[i%10];//优化for(i=0;i<=1111;i++)for(j=i;j<=1111;j++)if(a[i]+a[j]+a[i+j]==n)//减低了单个状态检查次数if(i==j)ans=ans+1;else ans=ans+2;cout<<ans<<endl;

例 完美立方数

描述

形如a^3= b^3 + c^3 + d^3的等式被称为完美立方等式。例如12^3= 6^3 + 8^3 + 10^3 。编写一个程序，对任给的正整数N (N≤100)，寻找所有的四元组(a, b, c, d)，使得a^3= b^3 + c^3 + d^3，其中a,b,c,d 大于 1, 小于等于N，且b<=c<=d。

输入

一个正整数N (N≤100)。

输出

每行输出一个完美立方。输出格式为：
a b c d
其中a,b,c,d所在位置分别用实际求出四元组值代入。

请按照a的值，从小到大依次输出。当两个完美立方等式中a的值相同，则b值小的优先输出、仍相同则c值小的优先输出、再相同则d值小的先输出。

样例输入

12

样例输出

6 3 4 5 
12 6 8 10

四重循环直接枚举

int main(){int a,b,c,sa,sb,sc,n,d,sd;cin>>n;for(a=3;a<=n;++a){sa=a*a*a;for(b=2;b<n;++b){sb=b*b*b;for(c=b;c<n;++c){sc=c*c*c;for(d=c;d<n;++d){sd=d*d*d;if(sa==sb+sc+sd)cout<<a<<" "<<b<<' '<<c<<' '<<d<<endl;}}}}return 0;
}

优化为三重循环

int main(){int a,b,c,sa,sb,sc,n,td;double d,sd;cin>>n;for(a=3;a<=n;++a){sa=a*a*a;for(b=2;b<a;++b){sb=b*b*b;for(c=b;c<a;++c){sc=c*c*c;if(sb+sc<sa){sd=sa-sb-sc;d=pow(sd,1.0/3);td=round(d);if(abs(d-td)<0.000001&&td>=c&&td<a)cout<<"Cube = "<<a<<", Triple = ("<<b<<','<<c<<','<<d<<')'<<endl;}}}}return 0;
}

 

连续子段和问题一

Description

　　给你n(n<=200000)个整数，然后要有m (m<=200000)个询问。每个询问两个整数x和y，问第x个数字到第y个数字所有数字之和。

Input

　　输入文件的第一行两个正整数N和M，分别表示序列长度和询问个数。
　　第2行包含N个绝对值不大于10000的整数A[i]，描述了这段序列。
　　接下来M行，每行两个整数x和y

Output

　　输出共计M行，每行一个整数表示该区间元素的和。

Sample Input

7 3

2 -4 3 -1 2 -4 3

1 7

2 4

3 6

Sample Output

1

-2

0

Hint

【数据规模与约定】
　　对于40%的数据，有N,M ≤ 2000。
　　对于100%的数据，有N,M ≤ 200000。

int a[200005],s;
int main(){int m,n,i,x,y;cin>>n>>m;for(i=1;i<=n;++i)scanf("%d",a+i);for(i=0;i<m;i++){//双重循环求区间数的和scanf("%d%d",&x,&y);s=0;for(int j=x;j<=y;j++)s+=a[j];printf("%d\n",s);}return 0;
}

#include<iostream>
#include<cstdio>
using namespace std;
int s[200005],a;
int main(){int m,n,i,x,y;cin>>n>>m;for(i=1;i<=n;++i){scanf("%d",&a);s[i]=s[i-1]+a;//存储前面i个数字之和}for(i=0;i<m;i++){//将双重循环降为了单循环scanf("%d%d",&x,&y);printf("%d\n",s[y]-s[x-1]);}return 0;
}

【枚举练习】子矩阵问题

Description

给定你一个N*M的数字矩形，要求在其中找一个R*C的权值最大矩阵。

Input

第一行两个整数N和M
第二行两个整数R和C。
接下来共计N行，每行M个用空格分开的整数（大于等于0且小于等于100）

Output

输出最大R*C的子矩阵的权值之和。

Sample Input

2  2
1  1
2  0
1  0

Sample Output

2

Hint

【数据规模】
　　对于80%数据,1 <= m,n <= 1000 
　　对于100%数据, 1 <= m,n <= 3000

没有优化的枚举

【 算法一 】 ：枚举每一个 R*C 的矩形区域的左上角坐标，然后求出该区域的权值之和。最后取所有区域中的最大值即可。此算法包含 4 重循环。
n 时间复杂度： O(N^4)   
int a[3005][3005];
int main(){int Max=0,a,i,j,k,l,s,n,m,r,c,i1,j1,ans;scanf("%d%d",&n,&m);scanf("%d%d",&r,&c);for(i=1;i<=n;i++)for(j=1;j<=m;j++){scanf("%d",&a[i][j]);}			for(i=1;i<=n-r+1;i++)for(j=1;j<=m-c+1;j++){ans=0;for(int k=i;k<r+i;k++)for(int l=j;l<c+j;l++)ans+=a[k][l];if(ans>Max)Max=ans;}printf("%d",Max); return 0;
}

优化后的枚举

【算法二】：我们设S[i,j]表示以(1,1)为左上角，(i,j)为右下角区域的权值之和，那么我们以(i,j)为右下角的R*C区域权值之和的计算公式为：

        Area[i,j]=S[i,j]+S[i-R,j-C]-S[i-R,j]-S[i,j-C]

其中S[i,j]的计算公式为：

        S[i,j]=S[i-1,j]+S[i,j-1]-S[i-1,j-1]+a[i,j]

       你可以随手画图出来，很容易即可证明上面两个式子。最后取Area[]中的最大值即可。

       时间复杂度：O(N^2)  

 

 

4565-562
4550565
45612865
65565123
92534532

 

4565-562
4550565
45612865
65565123
92534532
int s[3005][3005];
int main(){int Max=0,a,i,j,k,l,n,m,r,c,ans;scanf("%d%d",&n,&m);scanf("%d%d",&r,&c);for(i=1;i<=n;i++)for(j=1;j<=m;j++){scanf("%d",&a);s[i][j]=s[i][j-1]+s[i-1][j]-s[i-1][j-1]+a;}			for(i=r;i<=n;i++)for(j=c;j<=m;j++){ans=s[i][j]-s[i][j-c]-s[i-r][j]+s[i-r][j-c];if(ans>Max)Max=ans;}printf("%d",Max); return 0;
}

将四重循环优化为双重循环

 

 

 

 


http://chatgpt.dhexx.cn/article/UyEqD3j4.shtml

相关文章

传统人工势场法---经典算法

传统人工势场法---经典算法

网上代码很多&#xff0c;这个可以直接使用。 Xo[0 0];%起点位置 k50;%计算引力需要的增益系数 K0;%初始化 m15;%计算斥力的增益系数&#xff0c;都是自己设定的。 Po0.5;%障碍影响距离&#xff0c;当障碍和车的距离大于这个距离时&#xff0c;斥力为0&#xff0c;即不受该障碍…
阅读更多...
人工势场法（APF） —— Path Planning

人工势场法（APF） —— Path Planning

版权声明&#xff1a;本文为博主原创博文&#xff0c;未经允许不得转载&#xff0c;若要转载&#xff0c;请说明出处并给出博文链接 维基百科说&#xff1a;“人工势场法&#xff08;Artificial Potential Field&#xff0c; APF&#xff09;是一种将机器人的外形视为势场中的一…
阅读更多...
基于人工势场法的移动机器人路径规划研究（Matlab代码实现）

基于人工势场法的移动机器人路径规划研究（Matlab代码实现）

目录 &#x1f4a5;1 概述 &#x1f4da;2 运行结果 &#x1f389;3 参考文献 &#x1f468;‍&#x1f4bb;4 Matlab代码 &#x1f4a5;1 概述 路径规划是移动机器人领域的热点研究方向&#xff0c;人工势场法已在工业机器人路径规划中得到广泛应用&#xff0c;近年来正逐…
阅读更多...
11(0)-AirSim+四旋翼仿真-人工势场法避障

11(0)-AirSim+四旋翼仿真-人工势场法避障

1.基本原理 人工势场法的基本原理为&#xff0c;根据地图内障碍物、目标点等的分布&#xff0c;构造一个人工势场&#xff0c;无人机由势能较高的位置向势能较低的位置移动。就好比是一个电场&#xff0c;电场内不同位置的电势能不同&#xff0c;对带电物体产生的力也不同&…
阅读更多...
局部路径规划中的人工势场法

局部路径规划中的人工势场法

人工势场法是局部路径规划的一种比较常用的方法。这种方法假设机器人在一种虚拟力场下运动。 一、简介 如图所示&#xff0c;机器人在一个二维环境下运动&#xff0c;图中指出了机器人&#xff0c;障碍和目标之间的相对位置。 这个图比较清晰的说明了人工势场法的作用&#…
阅读更多...
matlab箭头梯度方向场,局部路径规划算法——人工势场法

matlab箭头梯度方向场,局部路径规划算法——人工势场法

人工势场法是由Khatib于1986年提出，其方法是将移动机器人所处的环境用势场来定义，通过位置信息来控制机器人的避障行驶，基本思想是构造目标位姿引力场和障碍物周围斥力场共同作用的人工势场，搜索势函数的下降方向来寻找无碰撞路径。人工势场法避障技术使得机器人的移动能很…
阅读更多...
基于人工势场法的车辆编队轨迹规划matlab仿真验证

基于人工势场法的车辆编队轨迹规划matlab仿真验证

给出了完整的MATLAB代码仿真&#xff1b;基于人工势场法编队的基本原理&#xff1a;通过构建车辆相对目标点的引力势场和斥力势场构建车辆所处地图下的整体势场&#xff0c;设置如图所示的势场图&#xff0c; 图中圆心为我们参考的目标点&#xff0c;其可以提供引力方向&#x…
阅读更多...
基于人工势场法的二维平面内无人机的路径规划的matlab仿真,并通过对势场法改进避免了无人机陷入极值的问题

基于人工势场法的二维平面内无人机的路径规划的matlab仿真,并通过对势场法改进避免了无人机陷入极值的问题

目录 1.算法描述 2.matlab算法仿真效果 3.MATLAB核心程序 4.完整MATLAB 1.算法描述 人工势场法原理是&#xff1a;首先构建一个人工虚拟势场&#xff0c;该势场由两部分组成&#xff0c;一部分是目标点对移动机器人产生的引力场&#xff0c;方向由机器人指向目标点&#xf…
阅读更多...
matlab人工势场法三维演示图,运动规划入门 | 5. 白话人工势场法，从原理到Matlab实现...

matlab人工势场法三维演示图,运动规划入门 | 5. 白话人工势场法，从原理到Matlab实现...

如何利用人工势场进行运动规划？ 1.1 引力势场(Attractive Potential Field) 人工势场这个特殊的势场并不是一个单一的场，其实它是由两个场叠加组合而成的，一个是引力场，一个是斥力场。 顾名思义引力势场是具有吸引的性质，会将机器人从起点处朝着终点处吸引，所以引力场的存…
阅读更多...
路径规划算法3 改进的人工势场法（Matlab）

路径规划算法3 改进的人工势场法（Matlab）

目录 传统人工势场 引力势场 斥力势场 合力势场 传统人工势场法存在的问题 改进的人工势场函数 Matlab代码实现 参考链接&#xff1a; [1]朱伟达. 基于改进型人工势场法的车辆避障路径规划研究[D]. 江苏大学, 2017. 1986年Khatib首先提出人工势场法&#xff0c;并将其应用在…
阅读更多...
【控制】人工势场法及人工势场函数

【控制】人工势场法及人工势场函数

目录 人工势场法-维基百科路径规划-人工势场法&#xff08;Artifical Potential Field&#xff09;引力场 (attractive/gravitation field)斥力场 (repulsive field)总场 【机器人路径规划】人工势场法PaperMatlab 代码自己编写的 Matlab1. 仅考虑引力的情况 人工势场法-维基百…
阅读更多...
移动机器人路径规划：人工势场法

移动机器人路径规划：人工势场法

人工势场法是一种原理比较简单的移动机器人路径规划算法&#xff0c;它将目标点位置视做势能最低点&#xff0c;将地图中的障碍物视为势能高点&#xff0c;计算整个已知地图的势场图&#xff0c;然后理想情况下&#xff0c;机器人就像一个滚落的小球&#xff0c;自动避开各个障…
阅读更多...
人工势场法matlab讲解_【机器人路径规划】人工势场法

人工势场法matlab讲解_【机器人路径规划】人工势场法

阅读本文需要的基础知识为： 理解机器人的构型空间。建议阅读：机器人运动规划中的C space怎样理解？为什么不直接在笛卡尔坐标系下运算呢？ 本文的实现程序与使用说明见我的学习工具箱：小明工坊：【个人开源】机器人运动规划学习工具箱使用说明 基本原理 1.概述 我们打两个比…
阅读更多...
学习笔记：人工势场法

学习笔记：人工势场法

一、算法简介 1986年Khatib首先提出人工势场法&#xff0c;并将其应用在机器人避障领域&#xff0c;而现代汽车可以看作是一个高速行驶的机器人&#xff0c;所以该方法也可应用于汽车的避障路径规划领域。 二、算法思想 1、人工势场法的基本思想是在障碍物周围构建障碍物斥力…
阅读更多...
人工势场法matlab讲解,传统人工势场法(matlab)

人工势场法matlab讲解,传统人工势场法(matlab)

【实例简介】 人工势场法路径规划是由Khatib提出的一种虚拟力法(Oussama Khatib，Real-Time obstacle Avoidance for Manipulators and Mobile Robots. Proc of The 1994 IEEE.)。它的基本思想是将机器人在周围环境中的运动，设计成一种抽象的人造引力场中的运动，目标点对移动…
阅读更多...
路径规划-人工势场法（Artifical Potential Field）

路径规划-人工势场法（Artifical Potential Field）

人工势场法是局部路径规划的一种比较常用的方法。这种方法假设机器人在一种虚拟力场下运动。 一、简介 如图所示&#xff0c;机器人在一个二维环境下运动&#xff0c;图中指出了机器人&#xff0c;障碍和目标之间的相对位置。 这个图比较清晰的说明了人工势场法的作用&#…
阅读更多...
人工势场法

人工势场法

文章目录 前言一、人工势场法二、简要理解 1.示例2.代码总结 前言 路径规划是移动机器人领域的一个重要组成部分&#xff0c;传统的路径规划代表算法包括 A*算法、Dijkstra 算法、人工势场法以及仿生学的蚁群算法。人工势场法是机器人路径规划算法中一种简单有效的方法。人工势…
阅读更多...
路径规划-人工势场法(Artificial Potential Field)

路径规划-人工势场法(Artificial Potential Field)

人工势场法是局部路径规划的一种比较常用的方法。这种方法假设机器人在一种虚拟力场下运动。 1. 简介 如图所示&#xff0c;机器人在一个二维环境下运动&#xff0c;图中指出了机器人&#xff0c;障碍和目标之间的相对位置。 这个图比较清晰的说明了人工势场法的作用&#xf…
阅读更多...
路径规划算法3.1 人工势场法APF

路径规划算法3.1 人工势场法APF

路径规划算法3.1 人工势场法APF 前言电场与电势场人工势场人工势场的构建梯度下降与局部最小问题后记 前言 人工势场法APF(Artificial Potential Field)&#xff0c;是非场经典的寻路方法&#xff0c;常用于移动机器人的局部路径规划&#xff0c;其主要思想是通过目标的引力与…
阅读更多...
【路径规划】局部路径规划算法——人工势场法（含python实现 | c++实现）

【路径规划】局部路径规划算法——人工势场法（含python实现 | c++实现）

文章目录 参考资料1. 算法简介2. 算法精讲2.1 引力势场2.2 斥力势场2.3 合力势场 3. 引力斥力推导计算4. 算法缺陷与改进4.1 目标不可达的问题4.2 陷入局部最优的问题4.3 解决方案4.3.1 改进障碍物斥力势场函数4.3.2 道路边界斥力势场 5. python实现6. c实现 参考资料 路径规划…
阅读更多...
推荐文章

Copyright @ 2022~2023