1.基本原理
人工势场法的基本原理为,根据地图内障碍物、目标点等的分布,构造一个人工势场,无人机由势能较高的位置向势能较低的位置移动。就好比是一个电场,电场内不同位置的电势能不同,对带电物体产生的力也不同,但这个力对物体运动的影响一定是由高势能到低势能的。只不过电场内的势能是物理上定义的,而人工势场的势能是根据我们的需求自己定义的。只需要定义合适的势函数,使得障碍物附近的势能大、目标点附近的势能小,就可以引导无人机飞往目标点而原理障碍物。这种方法不依赖于全局的障碍物信息,可以实现局部范围内的障碍物检测+避障。
这里使用常见的势函数定义,在python实现避障仿真,并参考文献[^1]中方法,针对人工势场法可能出现的局部极小值等问题进行改进。
2.势函数和势场
在单机飞行的避障中,对无人机产生影响的因素有障碍物和目标点,如果是多机编队还需考虑机间的影响。这里只考虑障碍物产生的斥力场和目标点产生的引力场。
常见的斥力势函数为
U r e p ( P ) = { 1 2 η ( 1 d ( P , P o b ) − 1 Q ) 2 , i f d ( P , P o b ) ≤ Q 0 , i f d ( P , P o b ) > Q U_{rep}(P)= \left\{\begin{aligned} \frac{1}{2}\eta(\frac{1}{d(P,P_{ob})}-\frac{1}{Q})^2,if\quad d(P,P_{ob})\leq Q \\0,if\quad d(P,P_{ob})> Q \end{aligned}\right. Urep(P)=⎩ ⎨ ⎧21η(d(P,Pob)1−Q1)2,ifd(P,Pob)≤Q0,ifd(P,Pob)>Q
其中 P P P为无人机当前坐标, P o b P_{ob} Pob为被计算势函数的障碍物坐标; Q Q Q为障碍物作用范围,该范围外的障碍物不会对无人机飞行产生影响; η \eta η为比例系数。
常见的引力势函数为
U a t t ( P ) = 1 2 ξ d 2 ( P , P g o a l ) U_{att}(P)=\frac{1}{2}\xi d^2(P,P_{goal}) Uatt(P)=21ξd2(P,Pgoal)
其中 P P P为无人机当前坐标, P g o a l P_{goal} Pgoal为目标点坐标, ξ \xi ξ为比例系数。
在以上势函数的定义下,物体距离目标点越近,目标点产生的引力势越小;物体距离障碍物越近,障碍物产生的引力势越大。物体向势较小的位置移动,故能接近目标点而远离障碍物。
得到势场内势的分布后,可以通过两种方法引导无人机飞行。一种为计算无人机周边位置的势,以势能最小的位置作为下一位置,由于只使用位置控制而不考虑速度和加速度,故在复杂场景下使用这种方法,得到的仿真轨迹不平滑。
另一种方法为对势能计算负梯度得到下降方向,以该方向作为加速度的方向,通过加速度-速度-位置的方法实现控制。具体计算方法为
F a t t = − ∇ U a t t ( P ) = − ξ ( P − P g o a l ) F r e p i = − ∇ U r e p ( P ) = { η ( 1 d ( P , P o b ) − 1 Q ) ⋅ 1 d ( P , P o b ) 3 ⋅ ( P − P o b ) , i f d ( P , P o b ) ≤ Q 0 , i f d ( P , P o b ) > Q F r e p = ∑ i F e q p i \begin{align} F_{att}&=-\nabla U_{att}(P)=-\xi(P-P_{goal}) \\F_{rep}^i&=-\nabla U_{rep}(P)= \left\{\begin{aligned} \eta(\frac{1}{d(P,P_{ob})}-\frac{1}{Q})·\frac{1}{d(P,P_{ob})^3}·(P-P_{ob}),if\quad d(P,P_{ob})\leq Q \\0,if\quad d(P,P_{ob})> Q \end{aligned}\right. \\F_{rep}&=\sum_i F_{eqp}^i \end{align} FattFrepiFrep=−∇Uatt(P)=−ξ(P−Pgoal)=−∇Urep(P)=⎩ ⎨ ⎧η(d(P,Pob)1−Q1)⋅d(P,Pob)31⋅(P−Pob),ifd(P,Pob)≤Q0,ifd(P,Pob)>Q=i∑Feqpi
3.方法改进
如果仅使用以上的方法,笔者遇到的主要问题有:
-
局部极小值,这是梯度下降算法中的一个常见问题。某一位置处势能低于其周边所有点,但是它并不是目标点,就好比是一个小球自上而下滚落,途中落入一个小坑,如下图所示(图片来源[^2])。由于物体移动的趋势为向势能更低处,所以此时它无论如何是无法离开这个极小值点的。

或者是如下图所示的情况,障碍物产生的斥力和目标点产生的引力方向相反,
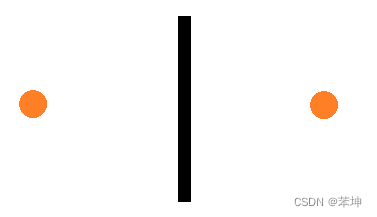
物体没有纵向的力,无法越过障碍物。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-b5jM8Ghv-1658911680145)(https://cdn.jsdelivr.net/gh/kun-k/blogweb/imageimage-20220715112653149.png)]
-
目标点与障碍物过于接近时,物体总是无法到达。由于障碍物存在斥力,目标点存在引力,如果此时斥力大于引力,则物体只能在目标点附近徘徊。如果设置参数、调小引力,则可能导致物体在移动过程中与障碍物过近或撞上障碍物。
-
目标点产生的势与距离正相关,物体距离目标点很远时,引力远大于斥力,导致斥力相对小、避障效果差。
接下来针对以上3个问题设计解决方案。
-
针对局部极小值问题,首先需对是否陷入局部极小进行检测,方法为在时间 t t t内计算物体的位移,如果该位移小于某一阈值,则认为陷入局部极小值。论文[^1]中提出的方法为,计算时间 t t t内物体相对目标点的位移
V r a = Δ X t = ∣ ∣ P 0 − P G ∣ ∣ − ∣ ∣ P 1 − P G ∣ ∣ t V_{ra}=\frac{\Delta X}{t}=\frac{||P_0-P_G||-||P_1-P_G||}{t} Vra=tΔX=t∣∣P0−PG∣∣−∣∣P1−PG∣∣
当 V r a V_{ra} Vra小于一阈值时认为陷入局部极小值。笔者尝试了两种解决方案。第一种为随机游走,在陷入局部极小值后物体随意改变移动方向一次,一段时间后再次进行判断。在很多情况下,这种方法可以时物体最终走出局部极小值点,但是由于移动方向是随机的,物体往往需要徘徊一段时间后才能离开。
第二种方法为论文[^1]中的方法,首先有计划地改变斥力的方向。
F r e p − n i = [ c o s θ − s i n θ s i n θ c o s θ ] F r e p i F_{rep-n}^i= \begin{bmatrix} cos\theta&-sin\theta\\sin\theta&cos\theta \end{bmatrix}F_{rep}^i Frep−ni=[cosθsinθ−sinθcosθ]Frepi
即将每个斥力都逆时针旋转一个角度 θ \theta θ。同时对引力进行调整
K v = 3 l 2 l + V r a K d = 3 ⋅ e − ( ∣ ∣ P − P G ∣ ∣ − 0.5 ) 2 2 + 1 K e ≥ 1 F a t t − n = K v K d K e F a t t K_v=\frac{3l}{2l+V_{ra}} \\K_d=3·e^{-\frac{(||P-P_G||-0.5)^2}{2}}+1 \\K_e\geq1 \\F_{att-n}=K_vK_dK_eF_{att} Kv=2l+Vra3lKd=3⋅e−2(∣∣P−PG∣∣−0.5)2+1Ke≥1Fatt−n=KvKdKeFatt
其中, l l l为移动步长,即无斥力影响下每个时间步的位移。而 V r a V_{ra} Vra总是小于步长的,所以 K v K_v Kv总是大于1,且随着 V r a V_{ra} Vra的减小而增大。在局部极小中起到的效果为,当物体陷入局部极小, V r a V_{ra} Vra会减小, K v K_v Kv增大,进而使引力的影响增大。同时斥力的方向改变,起到的效果示意如下,图片取自参考论文中。![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-CyolRSSR-1658911586576)(C:\Users\kun_s\AppData\Roaming\Typora\typora-user-images\image-20220715121303940.png)]](https://img-blog.csdnimg.cn/4c454a17565944e6a9c89832eebadf53.png)
此外,针对 θ \theta θ的选取,这里再做一些改进。论文中选择了 θ = 60 ° \theta=60° θ=60°对上图的情况进行测试,得到的效果很好。但是在很多情况下,固定角度 θ \theta θ不能离开局部极小值,陷入局部游走,或得到的解不理想,如下图所示的情况:


左侧是在 θ = 60 ° \theta=60° θ=60°下求解的情况,右侧为 θ = − 60 ° \theta=-60° θ=−60°,显然右侧的情况更好一些。考虑到 θ \theta θ的作用为增加侧向的力,使物体沿侧向离开障碍物的趋势更大,可以根据引力和斥力的方向设计 θ \theta θ的正负。如下图所示,沿逆时针方向,引力与斥力的角度小于180°时,斥力逆时针旋转,否则顺时针旋转。
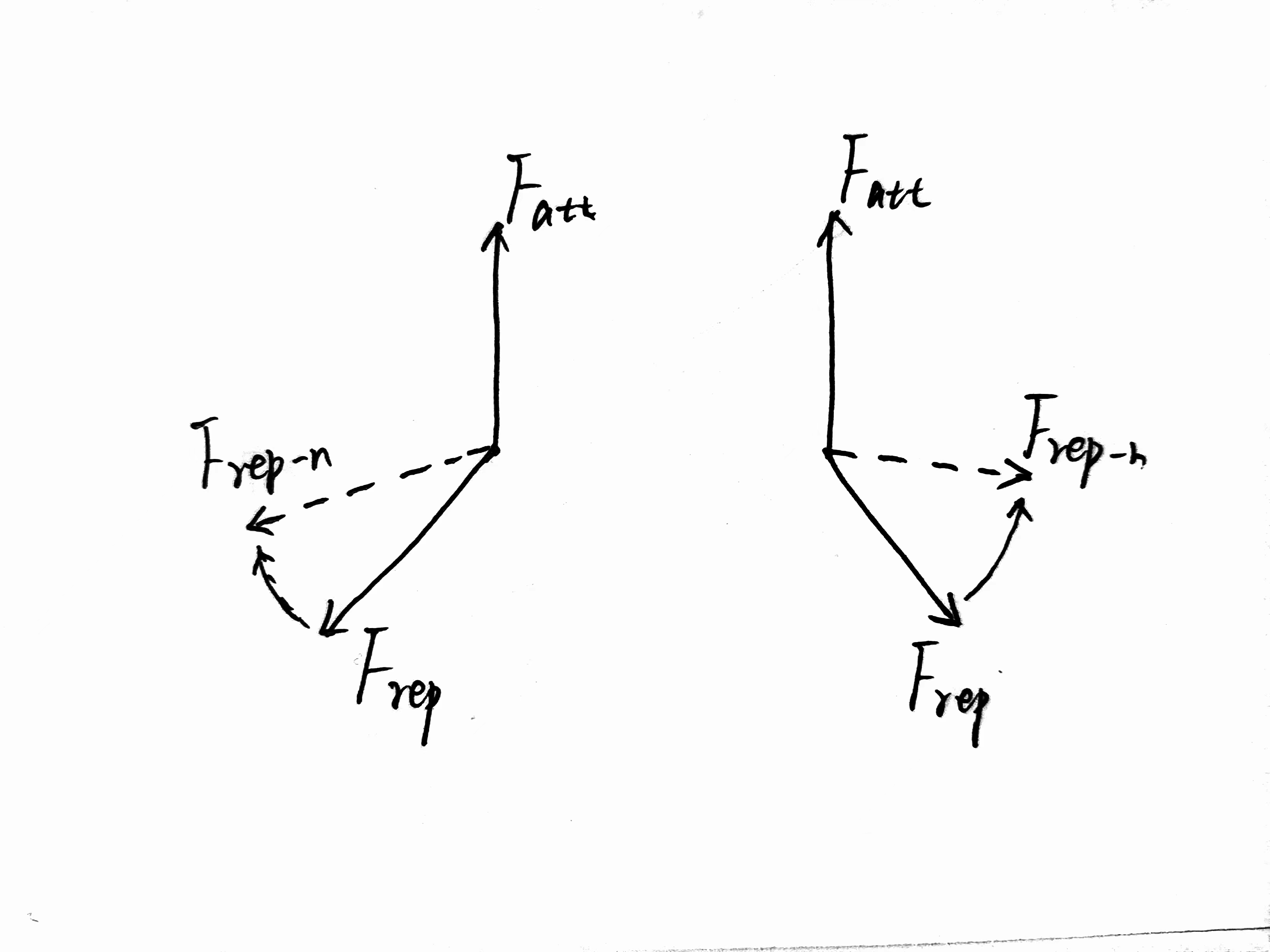
-
目标点与障碍物接近的问题,1.中的参数 K d K_d Kd可以解决该问题。
K d K_d Kd与物体距离目标点的距离相关,物体距离目标点的距离接近 0.5 0.5 0.5时, K d K_d Kd的值会比较大,而物体远离目标点时, K d K_d Kd指数减小至1。绘制 K d K_d Kd关于距离的变换图像为

故当物体距离目标点很近时,引力的作用显著增大,障碍物的作用相对减小。可以根据实际需求适当调整 K d K_d Kd中的参数。
- 目标点产生的势与距离成正相关,导致距离很远时斥力的作用相对小,避障效果差。一种常见的解决方法为,为斥力势乘以一个系数 ∣ ∣ P o b , P g o a l ∣ ∣ 2 k ||P_{ob},P_{goal}||_2^k ∣∣Pob,Pgoal∣∣2k, k k k可取2,此时相当于为斥力乘以障碍物到目标点的距离,使斥力大小也与距离相关。
4.实现过程和效果
经过以上改进后, F r e p F_{rep} Frep和 F a t t F_{att} Fatt的计算公式为:
K v = 3 l 2 l + V r a K d = 3 ⋅ e − ( ∣ ∣ P − P G ∣ ∣ − 0.5 ) 2 2 + 1 K e ≥ 1 F a t t = − K v K d K e ∇ U a t t ( P ) = − ξ ( P − P g o a l ) K_v=\frac{3l}{2l+V_{ra}} \\K_d=3·e^{-\frac{(||P-P_G||-0.5)^2}{2}}+1 \\K_e\geq1 \\F_{att}=-K_vK_dK_e\nabla U_{att}(P)=-\xi(P-P_{goal}) Kv=2l+Vra3lKd=3⋅e−2(∣∣P−PG∣∣−0.5)2+1Ke≥1Fatt=−KvKdKe∇Uatt(P)=−ξ(P−Pgoal)
F r e p F_{rep} Frep的计算公式为
F r e p i = − ∇ U r e p ( P ) = { η ( 1 d ( P , P o b ) − 1 Q ) ⋅ d ( P g o a l , P o b ) 2 d ( P , P o b ) 3 ⋅ ( P − P o b ) , i f d ( P , P o b ) ≤ Q 0 , i f d ( P , P o b ) > Q F r e p = ∑ i F e q p i \\F_{rep}^i=-\nabla U_{rep}(P)= \left\{\begin{aligned} \eta(\frac{1}{d(P,P_{ob})}-\frac{1}{Q})·\frac{d(P_{goal},P_{ob})^2}{d(P,P_{ob})^3}·(P-P_{ob}),if\quad d(P,P_{ob})\leq Q \\0,if\quad d(P,P_{ob})> Q \end{aligned}\right. \\F_{rep}=\sum_i F_{eqp}^i Frepi=−∇Urep(P)=⎩ ⎨ ⎧η(d(P,Pob)1−Q1)⋅d(P,Pob)3d(Pgoal,Pob)2⋅(P−Pob),ifd(P,Pob)≤Q0,ifd(P,Pob)>QFrep=i∑Feqpi
局部极小值下的 F r e p F_{rep} Frep为
F r e p − n = [ c o s θ − s i n θ s i n θ c o s θ ] F r e p F_{rep-n}= \begin{bmatrix} cos\theta&-sin\theta\\sin\theta&cos\theta \end{bmatrix}F_{rep} Frep−n=[cosθsinθ−sinθcosθ]Frep
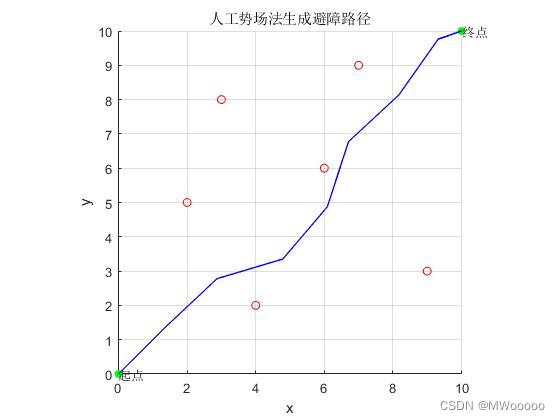
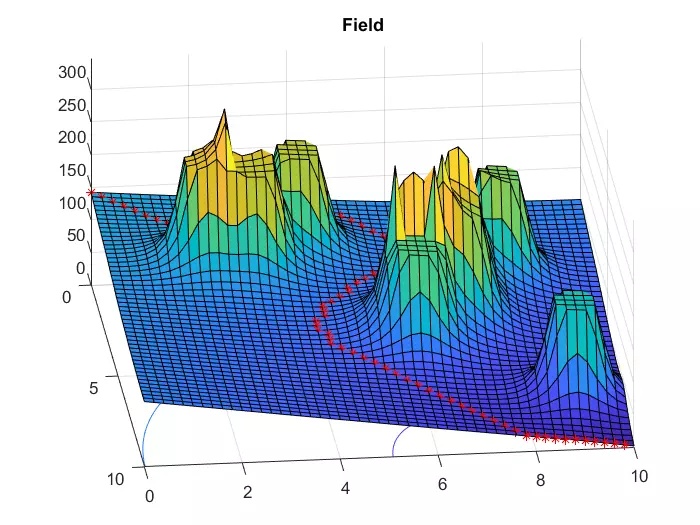
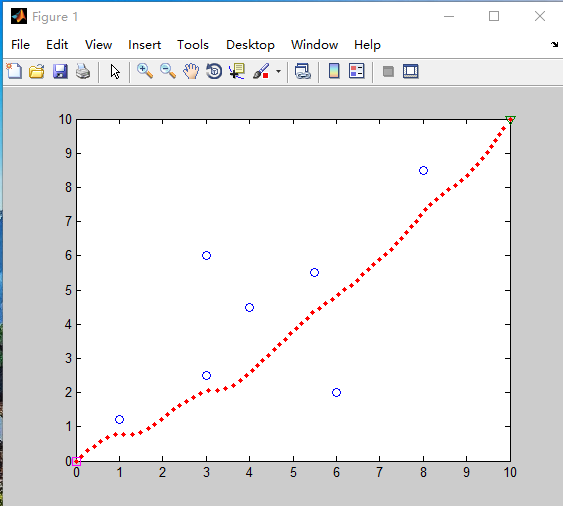
展示几组结果:
 |  |
|---|---|
 | 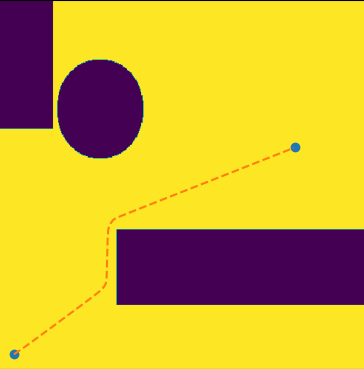 |
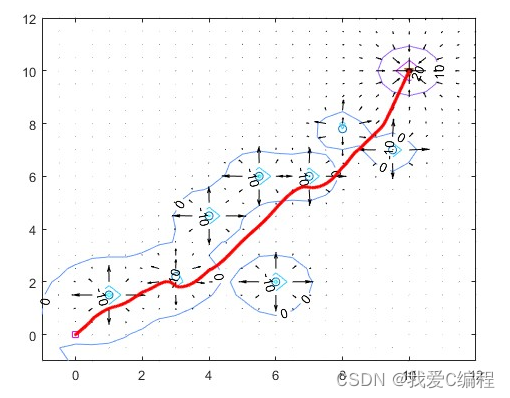
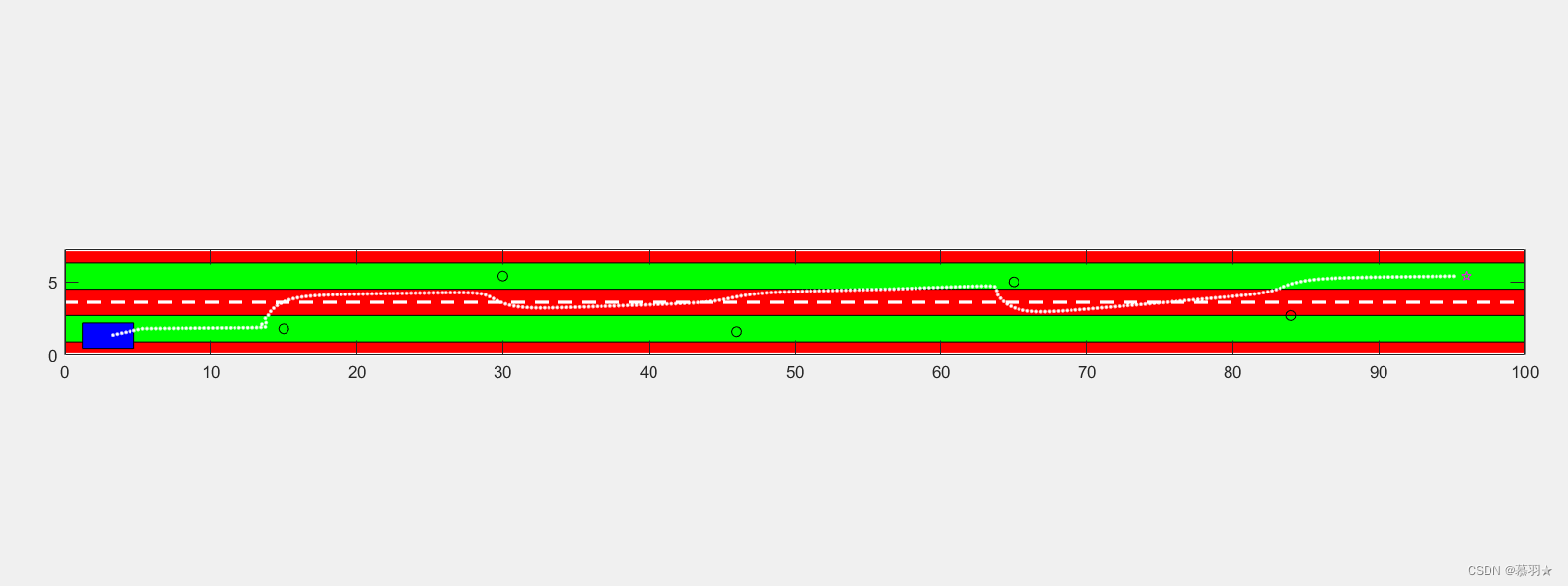
将避障与之前已经实现的轨迹规划结合,得到的结果为
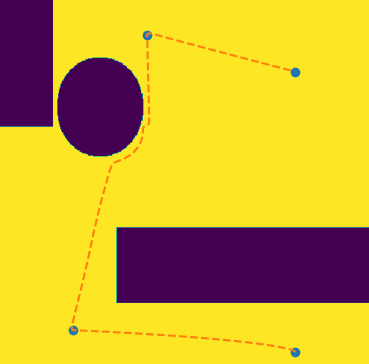 |  |
|---|
5.代码
'''
python_avoid_APF.py
人工势场法避障的python实现
'''import math
import matplotlib.pyplot as plt
import numpy as np
import cv2'''
P 初始位置
V 初始速度
P_aim 目标点
mymap 储存有障碍物信息的地图
Kg,Kr 避障控制器参数(引力,斥力)
Q_search 搜索障碍物距离
epsilon 误差上限
Vl 速率上限
Ul 控制器输出上限
dt 迭代时间
'''
def avoid_APF(P_start, V_start, P_aim, mymap, Kg=0.5, kr=20,Q_search=20, epsilon=2, Vl=2, Ul=2, dt=0.2):def distance(A, B):return math.sqrt((A[0] - B[0]) ** 2 + (A[1] - B[1]) ** 2)def myatan(a, b):if a == 0 and b == 0:return Noneif a == 0:return math.pi / 2 if b > 0 else math.pi * 3 / 2if b == 0:return 0 if a > 0 else -math.piif b > 0:return math.atan(b / a) if a > 0 else (math.atan(b / a) + math.pi)return math.atan(b / a + 2 * math.pi) if a > 0 else math.atan(b / a) + math.pidef isClockwise(a, b):da = b - aif 0 < da < math.pi or -math.pi * 2 < da < -math.pi:return Falsereturn True# 读取初始状态P_start = np.array(P_start) # 初始位置pos_record = [P_start] # 记录位置V_start = np.array(V_start).T # 初始速度# 地图尺寸size_x = mymap.shape[0]size_y = mymap.shape[1]# 设置绘图参数plt.axis('equal')plt.xlim(0, size_x)plt.ylim(0, size_y)# 绘制地图(障碍物和航路点)for i in range(mymap.shape[0]):for j in range(mymap.shape[1]):if mymap[i][j] == 0:plt.plot(i, j, 'o', c='black')plt.plot([P_start[0], P_aim[0]], [P_start[1], P_aim[1]], 'o')# 计算周边障碍物搜素位置direction_search = np.array([-2, -1, 0, 1, 2]) * math.pi / 4# 开始飞行pos_num = 0 # 已经记录的位置的总数P_curr = P_start # 当前位置V_curr = V_startob_flag = False # 用于判断局部极小值while distance(P_curr, P_aim) > epsilon:Frep = np.array([0, 0]) # 斥力angle_curr = myatan(V_curr[0], V_curr[1])for dir in direction_search:angle_search = angle_curr + dirfor dis_search in range(Q_search):P_search = [int(P_curr[0] + dis_search * math.sin(angle_search)),int(P_curr[1] + dis_search * math.cos(angle_search))]if not (0 <= P_search[0] < size_x and # 超出地图范围,地图内障碍,均视作障碍物0 <= P_search[1] < size_y andmymap[int(P_search[0])][int(P_search[1])] == 1):d_search = distance(P_curr, P_search) # 被搜索点与当前点的距离Frep = Frep + \kr * (1 / d_search - 1 / Q_search) / (d_search ** 3) * \(P_curr - P_search) * (distance(P_search, P_aim) ** 2)breakFatt = -Kg * (P_curr - P_aim) # 计算引力if pos_num >= 1:# 计算上两个时刻物体相对终点的位移,以判断是否陷入局部极小值p0 = pos_record[pos_num - 1]p1 = pos_record[pos_num - 2]Vra = (distance(p0, P_aim) - distance(p1, P_aim)) / dtif abs(Vra) < 0.6 * Vl: # 陷入局部极小值if ob_flag == False:# 之前不是局部极小状态时,根据当前位置计算斥力偏向角thetaangle_g = myatan(Fatt[0], Fatt[1])angle_r = myatan(Frep[0], Frep[1])if angle_r == None or angle_g == None:print('111')if isClockwise(angle_g, angle_r):theta = 15 * math.pi / 180else:theta = -15 * math.pi / 180ob_flag = True# 之前为局部极小,则继续使用上一时刻的斥力偏向角thetaFrep = [math.cos(theta) * Frep[0] - math.sin(theta) * Frep[1],math.sin(theta) * Frep[0] + math.cos(theta) * Frep[1]]else: # 离开局部极小值ob_flag = Falsel = VlKv = 3 * l / (2 * l + abs(Vra))Kd = 15 * math.exp(-(distance(P_curr, P_aim) - 3) ** 2 / 2) + 1Ke = 3Fatt = Kv * Kd * Ke * Fatt # 改进引力U = Fatt + Frep # 计算合力if np.linalg.norm(U, ord=np.inf) > Ul: # 控制器输出限幅U = Ul * U / np.linalg.norm(U, ord=np.inf)V_curr = V_curr + U * dt # 计算速度if np.linalg.norm(V_curr) > Vl: # 速度限幅V_curr = Vl * V_curr / np.linalg.norm(V_curr)P_curr = P_curr + V_curr * dt # 计算位置print(P_curr, V_curr, distance(P_curr, P_aim))pos_record.append(P_curr)pos_num += 1pos_record = np.array(pos_record).Tplt.plot(pos_record[0], pos_record[1], '--')plt.show()if __name__ == "__main__":# 读取地图图像并二值化img = cv2.imread('map.png')gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)retval, dst = cv2.threshold(gray, 0, 255, cv2.THRESH_OTSU)dst = cv2.dilate(dst, None, iterations=1)dst = cv2.erode(dst, None, iterations=4) / 255avoid_APF([0, 0], [1, 1], [80, 80], dst)
代码中参数比较多,可能会有些乱,但是我都增加了注释,思路也还可以,和上面说明的算法原理都是一致的。地图我使用Windows画图工具简单绘制,黑色表示障碍物。
目前还存在一些避障失败的情况,也没有设置安全距离,比较刁钻的情况下可能会直接跨越障碍物,之后还会继续调试改进。更加复杂的情况可以则使用路径规划,设置更多航路点再进行飞行。
也还没有实现三维空间内的避障,但是根据算法原理来看,应该是可以直接扩展到三维空间内的,这部分等拿到AirSim中无人机障碍物检测的接口后再继续修改调试。
参考来源:
[1] Li H . Robotic Path Planning Strategy Based on Improved Artificial Potential Field[C]// 2020 International Conference on Artificial Intelligence and Computer Engineering (ICAICE). 2020.
[2]https://mp.weixin.qq.com/s/JwpQAXDw9Rt1vlDDIZJMXA