本文收录于《深入浅出讲解自然语言处理》专栏，此专栏聚焦于自然语言处理领域的各大经典算法，将持续更新，欢迎大家订阅！
个人主页：有梦想的程序星空
个人介绍：小编是人工智能领域硕士，全栈工程师，深耕Flask后端开发、数据挖掘、NLP、Android开发、自动化等领域，有较丰富的软件系统、人工智能算法服务的研究和开发经验。
如果文章对你有帮助，欢迎
关注、
点赞、收藏、订阅。
1、决策树的背景
最早的决策树算法是由Hunt等人于1966年提出，Hunt算法是许多决策树算法的基础，包括ID3、C4.5和CART等。
决策树算法是一种有监督学习算法，利用分类的思想，根据数据的特征构建数学模型，从而达到数据的筛选，决策的目标。
2、决策树的原理
决策树( Decision Tree) 又称为判定树，是数据挖掘技术中的一种重要的分类与回归方法，它是一种以树结构（包括二叉树和多叉树）形式来表达的预测分析模型。其每个非叶节点表示一个特征属性上的测试，每个分支代表这个特征属性在某个值域上的输出，而每个叶节点存放一个类别。
一般，一棵决策树包含一个根节点，若干个内部结点和若干个叶结点。
叶结点对应于决策结果，其他每个结点对应于一个属性测试。每个结点包含的样本集合根据属性测试的结果划分到子结点中，根结点包含样本全集，从根结点到每个叶结点的路径对应了一个判定的测试序列。决策树学习的目的是产生一棵泛化能力强，即处理未见示例强的决策树。
使用决策树进行决策的过程就是从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，直到到达叶子节点，将叶子节点存放的类别作为决策结果。
3、决策树的构建
- 特征选择：选取有较强分类能力的特征。
- 决策树生成：典型的算法有 ID3 和 C4.5， 它们生成决策树过程相似， ID3 是采用信息增益作为特征选择度量， 而 C4.5 采用信息增益比率。
- 决策树剪枝：剪枝原因是决策树生成算法生成的树对训练数据的预测很准确， 但是对于未知数据分类很差， 这就产生了过拟合的现象。涉及算法有CART算法。
4、决策树的划分选择
熵：物理意义是体系混乱程度的度量。
信息熵：表示事物不确定性的度量标准，可以根据数学中的概率计算，出现的概率就大，出现的机会就多，不确定性就小（信息熵小）。
（1）信息增益（ID3使用的划分方式）
假设训练数据集和特征
，根据如下步骤计算信息增益：
第一步：计算数据集的经验熵：
其中，为第
类样本的数目，
为数据集D的数目。
第二步：计算特征对数据集
的经验条件熵
：
第三步：计算信息增益：
一般而言，信息增益越大，则意味着使用属性来进行划分所获得的“纯度提升” 越大。因此，我们可使用信息增益来进行决策树的划分属性选择。ID3决策树学习算法就是以信息增益为准则来选择划分属性的。
（2）信息增益率（C4.5所用划分准则）
特征对于数据集
的信息增益比定义为：
其中，称为数据集
关于
的取值熵。
增益率准则就可取值数目较少的属性有所偏好，因此，C4.5算法并不是直接选择增益率最大的候选划分属性，而是使用了一个启发式：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。
（3）基尼指数
分类问题中，假设有个类，样本点属于
的概率
，则概率分布的基尼指数：
二分类问题：
对给定的样本集合，基尼指数：
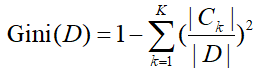
CART决策树使用“基尼指数”来选择划分属性。数据集的纯度可用基尼值来度量，
越小，则数据集的纯度越高。CART生成的是二叉树，计算量相对来说不是很大，可以处理连续和离散变量，能够对缺失值进行处理。
5、决策树的剪枝
剪枝：顾名思义就是给决策树 "去掉" 一些判断分支，同时在剩下的树结构下仍然能得到不错的结果。之所以进行剪枝，是为了防止或减少 "过拟合现象" 的发生，是决策树具有更好的泛化能力。
具体做法：去掉过于细分的叶节点，使其回退到父节点，甚至更高的节点，然后将父节点或更高的叶节点改为新的叶节点。
剪枝的两种方法：
预剪枝：在决策树构造时就进行剪枝。在决策树构造过程中，对节点进行评估，如果对其划分并不能再验证集中提高准确性，那么该节点就不要继续王下划分。这时就会把当前节点作为叶节点。
后剪枝：在生成决策树之后再剪枝。通常会从决策树的叶节点开始，逐层向上对每个节点进行评估。如果剪掉该节点，带来的验证集中准确性差别不大或有明显提升，则可以对它进行剪枝，用叶子节点来代填该节点。
注意：决策树的生成只考虑局部最优，相对地，决策树的剪枝则考虑全局最优。
6、决策树的优缺点
优点:
速度快:计算量相对较小，且容易转化成分类规则。只要沿着树根向下一直走到叶，沿途的分裂条件就能够唯一确定一条分类的谓词。
准确性高:挖掘出的分类规则准确性高，便于理解，决策树可以清晰的显示哪些字段比较重要。
非参数学习，不需要设置参数。
缺点：
决策树很容易过拟合，很多时候即使进行后剪枝也无法避免过拟合的问题，因此可以通过设置树深或者叶节点中的样本个数来进行预剪枝控制；
决策树属于样本敏感型，即使样本发生一点点改动，也会导致整个树结构的变化，可以通过集成算法来解决；
关注微信公众号【有梦想的程序星空】，了解软件系统和人工智能算法领域的前沿知识，让我们一起学习、一起进步吧！
