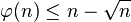一、欧拉函数
- 给定正整数n,欧拉函数φ(n)=不大于n且和n互质的正整数的个数(包括1)。
- φ(1)=1
- φ ( n ) = Σ i = 1 n [ g c d ( i , n ) = = 1 ] \varphi \left( n \right) =\varSigma_{i=1}^{n}\left[ gcd\left( i,n \right) ==1 \right] φ(n)=Σi=1n[gcd(i,n)==1]
完全余数集合: Zn={ 不大于n 且和n 互质的数} |Zn| =φ(n)
性质
(1)p为素数 ,则 φ( p)=p -1
质数与小于它的每一个,都构成互关系。 质数与小于它的每一个,都构成互关系。
(2)p为素数,正整数 n = p k n=p^k n=pk,则 φ ( n ) = p k − p k − 1 \varphi \left( n \right) =p^k-p^{k-1} φ(n)=pk−pk−1 或者写作 φ ( n ) = p k − 1 ( p − 1 ) = p k ( 1 − 1 p ) \varphi \left( n \right) =p^{k-1}\left(p-1 \right) =p^k\left( 1-\frac{1}{p} \right) φ(n)=pk−1(p−1)=pk(1−p1)
证明:
小于 p k p^k pk 的正整数个数为 p k − 1 p^k-1 pk−1个,其中与 p k p^k pk不互质的正整数有{p,2p,3p,4p,…, ( p k − 1 − 1 ) p (p^{k-1}-1)p (pk−1−1)p},共计 p k − 1 − 1 p^{k-1}-1 pk−1−1个
所以 φ ( n ) = p k − 1 − ( p k − 1 − 1 ) = p k − p k − 1 \varphi \left( n \right) =p^k-1-\left( p^{k-1}-1\right) =p^k-p^{k-1} φ(n)=pk−1−(pk−1−1)=pk−pk−1
(3)两个素数 p,q ,n=p * q,则 φ(n) =( p-1) * ( q-1)
证明:
Zn={1,2,3,…,n-1}-{p,2p,3p,…,(q-1)p}-{q,2q,3q,…,(p-1)q}
φ(n)=(n-1)-(q-1)-(p-1)
=(p * q-1)-(p-1)-(q-1)
=(p * q-p)-(q-1)
=p(q-1)-(q-1)
=(p-1)(q-1)

(4)当b时质数,a%b=0,则φ(ab)=φ(a)b
证明:
设 a = k b n a=kb^n a=kbn 且gcd(k,b)=1,则 φ ( a ) = φ ( k ) φ ( b n ) φ(a)=φ(k)φ(b^n) φ(a)=φ(k)φ(bn), φ ( k ) = φ ( a ) φ ( b n ) φ(k)=\frac{φ(a)}{φ(b^n)} φ(k)=φ(bn)φ(a)
φ ( a b ) = φ ( k b n + 1 ) = φ ( k ) φ ( b n + 1 ) = φ ( a ) φ ( b n ) φ ( b n + 1 ) = φ ( a ) ( φ ( b n + 1 ) φ ( b n ) ) = φ ( a ) b φ(ab)=φ(kb^{n+1})=φ(k)φ(b^{n+1})=\frac{φ(a)}{φ(b^n)}φ(b^{n+1})=φ(a)(\frac{φ(b^{n+1})}{φ(b^n)})=φ(a)b φ(ab)=φ(kbn+1)=φ(k)φ(bn+1)=φ(bn)φ(a)φ(bn+1)=φ(a)(φ(bn)φ(bn+1))=φ(a)b
φ ( b n + ! ) = b n + 1 − b n , φ ( b n ) = b n − b n − 1 φ(b^{n+!})=b^{n+1}-b^n,φ(b^n)=b^n-b^{n-1} φ(bn+!)=bn+1−bn,φ(bn)=bn−bn−1
(5)任意正整数n: n = p 1 a 1 p 2 a 2 . . . p m a m n=p^{a_1}_1p^{a_2}_2...p^{a_m}_m n=p1a1p2a2...pmam ( p i p_i pi 为素数), φ ( n ) = n ( 1 − 1 p 1 ) ( 1 − 1 p 2 ) . . . ( 1 − 1 p m ) φ(n)=n(1-\frac{1}{p_1})(1-\frac{1}{p_2})...(1-\frac{1}{p_m}) φ(n)=n(1−p11)(1−p21)...(1−pm1)
证明:
φ ( n ) = φ ( p 1 a 1 ) φ ( p 2 a 2 ) . . . φ ( p m a m ) φ(n)=φ(p^{a_1}_1)φ(p^{a_2}_2)...φ(p^{a_m}_m) φ(n)=φ(p1a1)φ(p2a2)...φ(pmam)
= ( p 1 a 1 p 2 a 2 . . . p m a m ) ( 1 − 1 p 1 ) ( 1 − 1 p 2 ) . . . ( 1 − 1 p m ) =(p^{a_1}_1p^{a_2}_2...p^{a_m}_m)(1-\frac{1}{p_1})(1-\frac{1}{p_2})...(1-\frac{1}{p_m}) =(p1a1p2a2...pmam)(1−p11)(1−p21)...(1−pm1) (由性质(2)知)
= n ( 1 − 1 p 1 ) ( 1 − 1 p 2 ) . . . ( 1 − 1 p m ) =n(1-\frac{1}{p_1})(1-\frac{1}{p_2})...(1-\frac{1}{p_m}) =n(1−p11)(1−p21)...(1−pm1) (被称为欧拉函数计算公式)
如何进一步理解欧拉函数计算公式?

(6)欧拉函数递推式:可用于线性求1~n所有数的欧拉函数
给定质数p,满足p|x,
若p2|x不成立,则 φ ( x ) = φ ( x p ) ∗ ( p − 1 ) φ(x)=φ(\frac{x}{p})*(p-1) φ(x)=φ(px)∗(p−1)
若p2|x成立,则 φ ( x ) = φ ( x p ) ∗ p φ(x)=φ(\frac{x}{p})*p φ(x)=φ(px)∗p
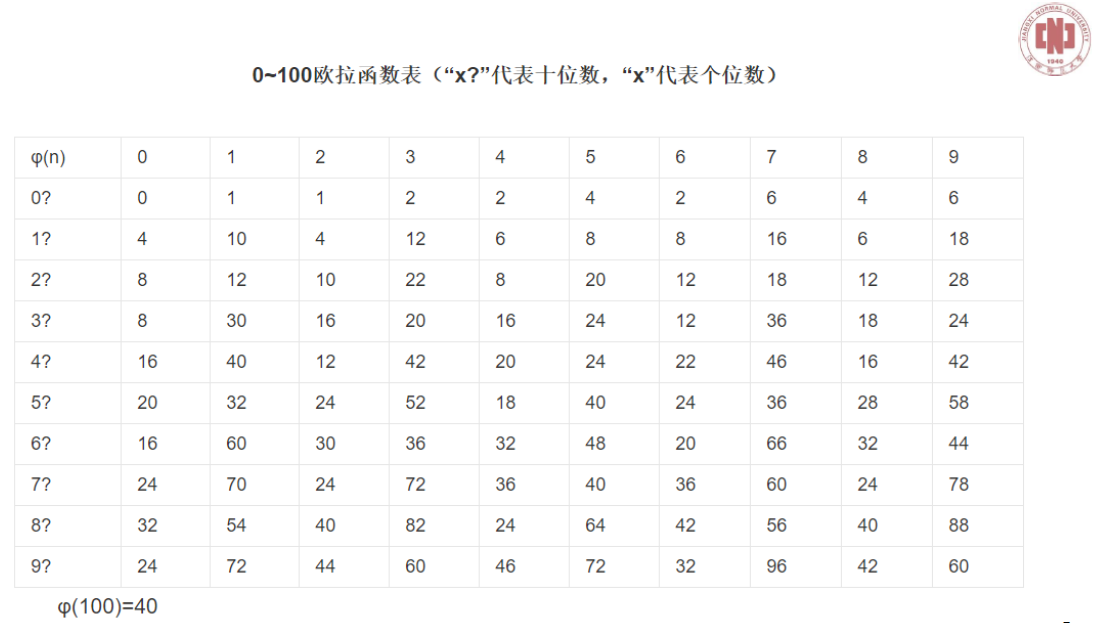
欧拉函数打表:
int primes[N], euler[N], cnt;
bool st[N];
void get_eulers(int n)
{euler[1] = 1;for (int i=2; i <= n; i++ ){if ( !st[i] ){primes[cnt++] = i;euler[i] = i-1;}for ( int j=0; primes[ j] <= n/i; j++ ){st[ primes[ j]*i ] = true;if ( i % primes[ j] == 0 ) {euler[ i*primes[ j] ] = euler[i] * primes[ j];break;}euler[ i*primes[ j] ] = euler[i] * ( primes[j]-1 );}}
}
(7)整数n 等于n的所有约数(包括1和n)的欧拉函数之和,即 n = Σ d ∣ n φ ( d ) n=\varSigma_{d|n}\varphi \left( d \right) n=Σd∣nφ(d)


(8)给定整数n,所有小于n且与n互质的数的和是 n ∗ φ ( n ) 2 n∗\frac{φ(n)}{2} n∗2φ(n)
-
小于n的与n互质数i 和n-i 总是成对出现,且它们的和是n;
小于n的且与n互质 数的个数是φ(n)。
-
所以, Σ i = 1 n − 1 i [ g c d ( i , n ) = = 1 ] = n ∗ φ ( n ) / 2 \varSigma _{i=1}^{n-1}i\left[ gcd\left( i,n\right) ==1 \right] =n*\varphi \left( n \right) /2 Σi=1n−1i[gcd(i,n)==1]=n∗φ(n)/2,还需分析i=n-i的情况 (即n为偶数情况)
(1)如果n是奇数,i≠n-i
(2)如果n是大于2的偶数,gcd(n,n/2)≠1
(3)如果n是2, n ∗ φ ( n ) 2 = 2 ∗ 1 2 = 1 n* \frac{φ(n)}{2}=2*\frac{1}{2}=1 n∗2φ(n)=2∗21=1
性质:若 gcd(n,i)=1,则 gcd(n,n-i)=1(1≤i≤n)
反证法:
如果存在k≠1 使gcd(n,n-i)=k,那么(n-i)%k=0,n%k=0,n=k * j
→ (k * j-i)%k=0 → k * j%k-i%k=0 → i%k=0
因为k是n的因子, i%k=0 → gcd(n,i)=k,与原命题矛盾。

二、欧拉定理
1.欧拉定理
正整数a和n互质,有 a φ ( n ) ≡ 1 m o d n a^{φ(n)}≡1\ mod\ n aφ(n)≡1 mod n
证明:
1.令Zn={ x 1 , x 2 , . . . , x φ ( n ) x_1,x_2,...,x_{φ(n)} x1,x2,...,xφ(n) }为 φ(n)个<n且与n互质的数 x i x_i xi ,
构造S={ a x 1 ax_1 ax1%n , a x 2 ax_2 ax2%2 , … a x φ ( n ) ax_{φ(n)} axφ(n)%n}
即要证:Zn=S
(1)a与n互质 且 x i x_i xi与n互质 → a x i ax_i axi 与n互质 → a x i m o d n ∈ Z n ax_i\ mod\ n∈Zn axi mod n∈Zn
(2)若i≠j,则 x i ≠ x j x_i≠x_j xi=xj → a x i ax_i axi%n ≠ a x j ax_j axj%n (否则由模运算消去律, x i = x j x_i=x_j xi=xj)
2.证: a φ ( n ) x 1 x 2 . . . x φ ( n ) m o d n ≡ ( a x 1 ) ( a x 2 ) . . . ( a x φ ( n ) m o d n ) a^{φ(n)}x_1x_2...x_{φ(n)}\ mod\ n≡(ax_1)(ax_2)...(ax_{φ(n)}\ mod\ n) aφ(n)x1x2...xφ(n) mod n≡(ax1)(ax2)...(axφ(n) mod n)
≡ ( a x 1 m o d n ) ( a x 2 m o d n ) . . . ( a x φ ( n ) m o d n ) ≡ x 1 x 2 . . . x φ ( n ) m o d n ≡(ax_1\ mod\ n)(ax_2\ mod\ n)...(ax_{φ(n)}\ mod\ n)≡x_1x_2...x_{φ(n)}\ mod\ n ≡(ax1 mod n)(ax2 mod n)...(axφ(n) mod n)≡x1x2...xφ(n) mod n
所以有: a φ ( n ) x 1 x 2 . . . x φ ( n ) ≡ x 1 x 2 . . . x φ ( n ) m o d n a^{φ(n)}x_1x_2...x_{φ(n)}≡x_1x_2...x_{φ(n)}\ mod\ n aφ(n)x1x2...xφ(n)≡x1x2...xφ(n) mod n
因为 x i x_i xi (1≤i≤φ(n) )与n互质,所以 a φ ( n ) ≡ 1 m o d n a^{φ(n)}≡1\ mod\ n aφ(n)≡1 mod n (消去律)
模运算消去律:若gcd(c,p)=1,则ac≡bc mod p → a≡b mod p
证明:
ac ≡ bc mod p → c(a -b) = kp
gcd (c,p )=1 → 存在 2种可能: 1) c 能整除 k 2)a=b
如果 2) 成立,命题 a ≡ b mod p 显然成立
如果 1) 成立 ,则 k = ck‘
→ c(a -b)= kp 可改写为 c(a -b) = ck‘p
所以 a-b= k‘p,得出 a ≡ b mod p
2.费马小定理
若正整数a与素数p互质,则有 a p − 1 ≡ 1 ( m o d p ) a^{p-1}≡1(mod\ p) ap−1≡1(mod p),或写为 a p ≡ a ( m o d p ) a^p≡a(mod\ p) ap≡a(mod p)
φ§=p-1
费马小定理求逆元
若p为素数, a p − 1 ≡ 1 ( m o d p ) a^{p-1}≡1(mod\ p) ap−1≡1(mod p) → a a p − 2 ≡ 1 ( m o d p ) aa^{p-2}≡1(mod\ p) aap−2≡1(mod p)
欧拉定理求逆元
若a,p互素, a φ ( p ) ≡ 1 ( m o d p ) a^{φ(p)}≡1(mod\ p) aφ(p)≡1(mod p) → a a φ ( p ) − 1 ≡ 1 ( m o d p ) aa^{φ(p)-1}≡1(mod\ p) aaφ(p)−1≡1(mod p)
3.整数的阶
设a与n是互质的正整数,使得 a x ≡ 1 a^x≡1 ax≡1 mod n 成立的最小正整数x 称为整数a模n的阶,记为 o r d n a ord_n\ a ordn a

4.原根
设a与n是互质的正整数且n>0,则当 o r d n a ∣ φ ( n ) ord_n\ a|φ(n) ordn a∣φ(n) 时,称a为模n的原根,即a满足 a φ ( n ) ≡ 1 m o d n a^{φ(n)}≡1\ mod\ n aφ(n)≡1 mod n
特点:
-
所有的素数p一定有原根,且模p的原根个数为φ(p-1)。
-
不是所有的整数都有原根。
原根存在的条件
模m有原根的充要条件:m=2, 4, p t p^t pt, 2 ⋅ p t 2⋅p^t 2⋅pt ,其中p为奇质数,t为正整数
性质
-
设a与m是互质的正整数且m>0,则如果a是模m的一个原根,那么整数a, a 2 a^2 a2 , … , a φ ( m ) a^{φ(m)} aφ(m) 构成模m的简化剩余系。
-
设g 是模m的一个原根,i 是一个正整数,那么 g i g^i gi 也是模m的原根的充要条件是gcd(i,φ(m))=1 。
o r d m ( a u ) ord_m(au) ordm(au) 的性质:若u是一个正整数,且 o r d m a = t ord_ma=t ordma=t ,则 o r d m ( a u ) = t g c d ( t , u ) ord_m(a^u)=\frac{t}{gcd(t,u)} ordm(au)=gcd(t,u)t
推论:当正整数m 有原根时,则有φ(φ(m)) 个原根。
- 一个数的最小原根的不超过 m 1 4 m^{\frac{1}{4} } m41
求最小原根:依次枚举2~ m 1 4 m^{\frac{1}{4} } m41 判断即可
求所有原根:枚举最小原根的指数即可
5.计算大数取模
求 (ab)%m 的值,其中a,b都可能很大
快速幂求 (ab)%m
-
(ab)%m =(a%m)b)%m
-
用带模快速幂计算,时间复杂度O(log b);但当b是超大数时,我们还需要更快的算法。

三、欧拉降幂
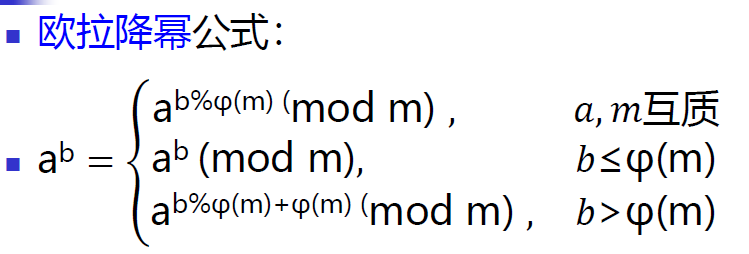

四、习题
Euler Function HDU-6322
Farey Sequence POJ-2478
LCM SUM SPOJ-5971
Longge的问题 BZOJ-2705
Count a × b HDU-5528
The Luckiest number POJ-3696
Period of Inf. Bin. Exp. POJ-3358
Sum HDU-4704
A ternary string 2018牛客暑期训练营
Xyjj’s sequence 2019ICPC南昌邀请赛
Visible Lattice Points POJ-3090 (欧拉函数)
Stern-Brocot Tree HDU-4556 (法里数列)
沙拉公主的困惑 SDOI2008 (欧拉函数+模逆)
欧拉心算 BZOJ-4804 (欧拉函数)
Bi-shoe and Phi-shoe LightOJ-1370 (欧拉函数)
BZOJ-4173 (欧拉函数)
Description has only two Sentences HDU-3307 (欧拉定理)
上帝与集合的正确用法 BZOJ-3884 (欧拉降幂)
Brute-force Algorithm HDU-3221 (欧拉降幂+矩阵快速幂)
子序列 (欧拉降幂)
五、相关链接
原根