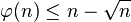在之前的博客中介绍过一次协方差矩阵：

浅谈协方差矩阵_Yunlong_Luo的博客-CSDN博客

这次希望在之前的基础上，把协方差矩阵介绍的更清楚一些，本文的很多素材来自于：

A geometric interpretation of the covariance matrix

期望和方差

期望和方差是描述一组数据分布的统计上的指标，如下图所示：

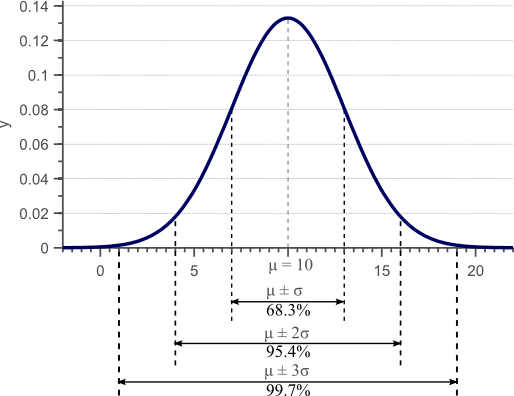
图1

这个数据只是1维的，什么叫1维的，可以理解为这个数据只有一个属性，比如一组数据都是描述x等于多少。方差定义的公式为：

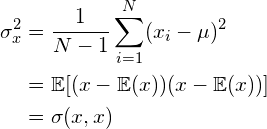
但是如果这组数据是2维的或者高维的，比如下图：

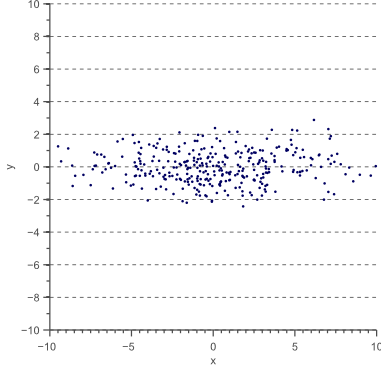
图2

如何描述上面这组数据的分布呢？这组数据包含了x和y两个属性，可以分别计算x的方差和y方差。很显然这组数据x的方差和y的方差不一样，x的分布更散乱，所以x的方差更大。

协方差

只用方差可以描述一个1维的数据的分布情况，但是2维或者高维的数据，只用方差能完整的描述分布情况吗？比如下图

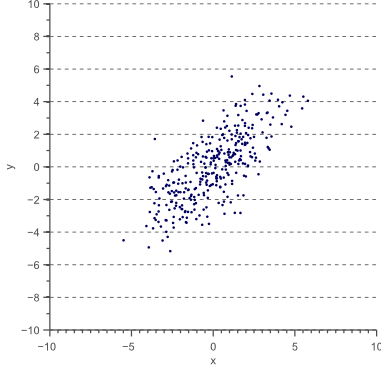
图3

图2和图3的差别是什么？差别在于这个数据的分布发生了旋转，怎么去理解这种旋转呢？

通常的解释是称这种关系叫做相关性，x和y之间存在相关性，用协方差来表示这种关系：

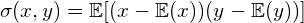
但是这个解释还是太抽象了，不好理解。

协方差矩阵

2维的协方差矩阵的示例如下

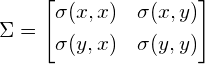
推导过程如下

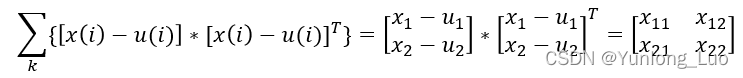
所以x11描述的是第一组的数据的波动程度，x22表示第二组的数据的波动程度。

 但是x12和x21表示什么呢？通过公式上来理解就是协方差，表示的是x1和x2这两组数据的相关性。

但是到这依然不好理解协方差的几何含义。继续往下看。

协方差矩阵的特征分解

协方差矩阵定义了数据的散布（方差）和方向（协方差）。所以，如果我们想用一个向量和它的大小来表示协方差矩阵，我们应该简单地尝试找到指向数据最大传播方向的向量，并且它的大小等于这个传播（方差）方向。

根据特征值和特征向量的定义：

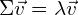
v是特征向量，lambda是特征值。

协方差矩阵的最大特征向量总是指向数据方差最大的方向，这个向量的大小等于对应的特征值。第二大特征向量始终与最大特征向量正交，并指向数据的第二大传播方向。

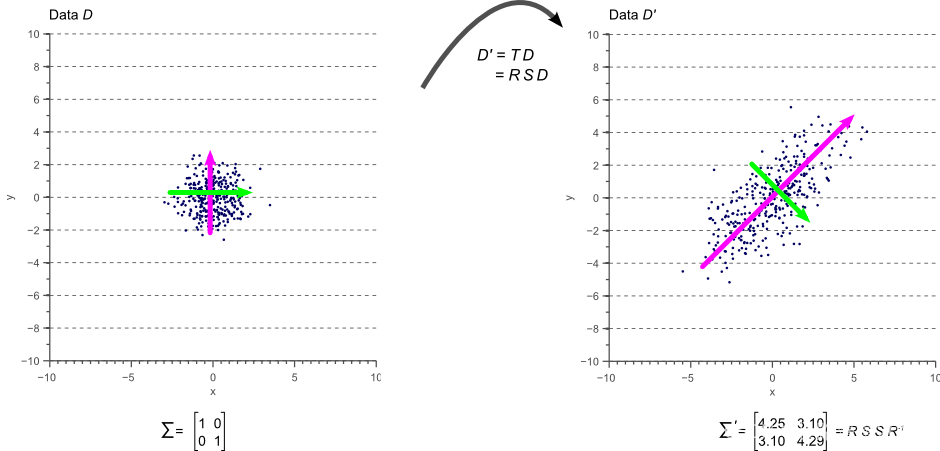
下面来看几个图：

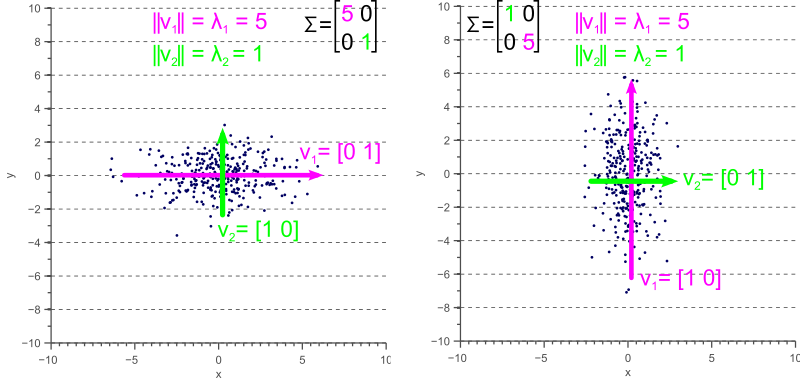
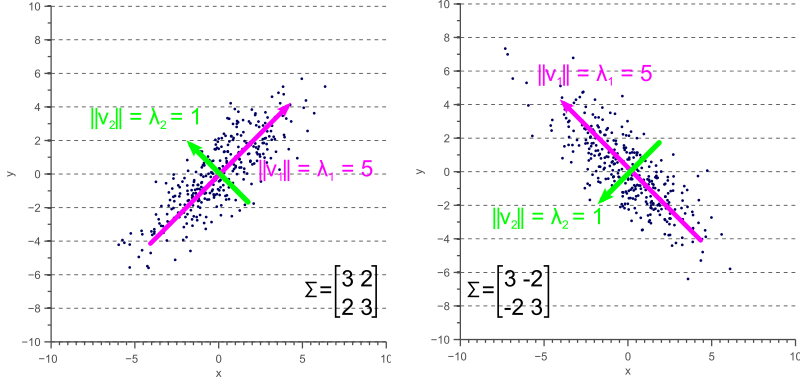
这几个图中数据的分布特征没有变，只是进行了旋转，我们看到协方差矩阵跟着变了，但是特征值没有变。

既然说协方差矩阵定义了数据的散布和方向，是如何定义的呢？其实是协方差矩阵的特征分解结果中特征向量表示方向，特征值表示所对应的方向的数据分布的方差。

比如特征向量的方向就是x轴和y轴的方向，那么协方差矩阵的对角元素的值就是方差值，也就是特征值，此时非对角元素为0。

但是特性向量的方向和x轴和y轴不相同时，协方差的对角元素的值不等于方差值，非对角元素不一定0。

如何进一步理解呢？

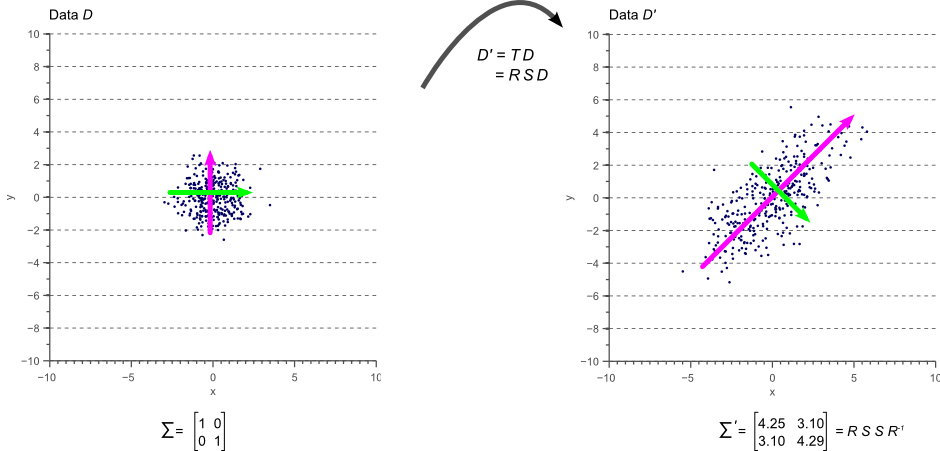
通过这张图可以看到，可以通过对一个协方差矩阵进行变换得到新的数据分布特征的方向特征。数据分布特征可以通过改变特征值，方向特征可以改变特征向量。怎么改变呢？

特征分解，得到特征向量V和对应的特征值L

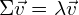
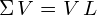
协方差矩阵可以写成特征向量和特征值的表达式

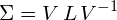
S等于根号L

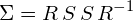
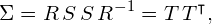
最后得出的结果显示，对一个协方差矩阵可以修改特征值和特征向量进行旋转和缩放。