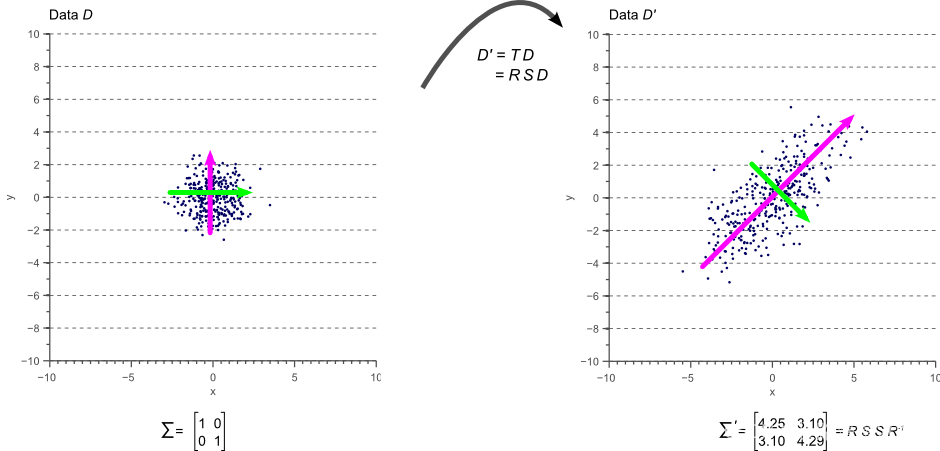
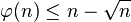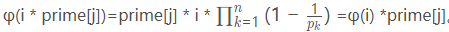协方差矩阵-Covariance Matrix

article/2025/11/10 22:24:23

首先我们要明白，协方差实际是在概率论和统计学中用于衡量两个变量的总体误差,当然方差是协方差的一种特殊情况，即当两个变量是相同情况。它表示的是两个变量的总体的误差，这与只表示一个变量误差的方差不同。如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。

而矩阵就比较直接了，就是一个按照长方阵列排列的复数或实数集合。看看下面定义

这m×n 个数称为矩阵A的元素，简称为元，数aij位于矩阵A的第i行第j列，称为矩阵A的(i,j)元，以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n，m×n矩阵A也记作Amn。

科普over了之后我们回归到正题，协方差矩阵是什么？

协方差矩阵在统计学和机器学习中随处可见，一般而言，可视作方差和协方差两部分组成，即方差构成了对角线上的元素，协方差构成了非对角线上的元素。说白了，就是方差及协方差在一个矩阵中表现出来。这里就体现了变量间的联动关系。

这里我们同样以一个例子切入

1.先解方差

$\sigma_{x} ^{2}= \frac{1}{3}*((179-180.3)^{2} +(187-180.3)^{2} +(175-180.3)^{2} ) = 24.87$

$\sigma_{y} ^{2}= \frac{1}{3}*((74-75)^{2} +(80-75)^{2} +(71-75)^{2} ) = 14$

$\sigma_{z} ^{2}= \frac{1}{3}*((33-30.7)^{2} +(31-30.7)^{2} +(28-30.7)^{2} ) = 4.22$

2.再看下协方差

$\sigma _{x}\sigma _{y} = \frac{1}{3}((179-180.3)*(74-75)+(187-180.3)*(80-75)+(175-180.3)*(71-75)) = 18.7$

$\sigma _{x}\sigma _{z} = \frac{1}{3}((179-180.3)*(33-30.7)+(187-180.3)*(31-30.7)+(175-180.3)*(28-30.7)) = 4.4$

$\sigma _{y}\sigma _{z} = \frac{1}{3}((74-75)*(33-30.7)+(80-75)*(31-30.7)+(71-75)*(28-30.7)) = 3.3$

3.来构建协方差矩阵P(把方差和协方差结果带入，例子只有3组数据就是如下图所示)

$P = \begin{bmatrix} \sigma _{x}^{2} & \sigma _{x}\sigma _{y} & \sigma _{x}\sigma _{z}\\ \sigma _{y}\sigma _{x} & \sigma _{y}^{2}& \sigma _{y}\sigma _{z} \\ \sigma _{z}\sigma _{x} & \sigma _{z}\sigma _{y} & \sigma _{z}^{2} \end{bmatrix} = \begin{bmatrix} 24.89&18.7 &4.4 \\18.7 &14 &3.3 \\ 4.4&3.3 &4.22 \end{bmatrix}$

我们在看看定义，即方差构成了对角线上的元素，协方差构成了非对角线上的元素。

对角上元素：方差

那么如何通过矩阵的运算，来计算协方差并且如何使用它来解决实际问题呢？

首先我们要求一个过渡矩阵，再通过它来算得协方差矩阵

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

$a = \begin{bmatrix} x_{1}& y_{1} &z_{1} \\ x_{2}& y_{2} &z_{2} \\ x_{3}& y_{3} &z_{3} \end{bmatrix} - \frac{1}{3}\begin{bmatrix} 1 &1 &1 \\ 1& 1 &1 \\ 1& 1 & 1 \end{bmatrix}\begin{bmatrix} x_{1}& y_{1} &z_{1} \\ x_{2}& y_{2} &z_{2} \\ x_{3}& y_{3} &z_{3} \end{bmatrix}$