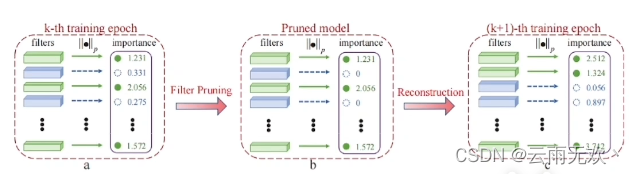
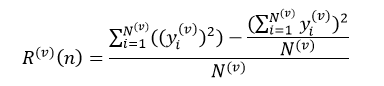在讲α、β剪枝法之前,我们先了解一下极大极小值算法;因为α、β剪枝法是为了简化极大极小值的计算而提出的。
极大极小值法
Minimax算法 又名极小化极大算法,是一种找出失败的最大可能性中的最小值的算法(即最小化对手的最大得益)。通常以递归形式来实现。这一算法通常是用于零和博弈中,即双方的获利与损失之和永远为零。为了使己方利益最大化,我们会选择对自己最有利的条件,而尽可能地让对方陷入不利的条件中。并且该算法的前提是,对方是绝对聪明的,即对方不会在决策时出现失误。
因此,在极大极小值算法中,我们可以假定本方为A,而对方为B;同时我们假定所有的数值都代表本方获胜的值。当本方进行决策时,我们一定希望这个值越大越好,即我们会尽可能地让α的值变大;而当轮到对方进行决策时,对方一定希望这个值越小越好,即对方会尽可能地让β的值变小(要记住,无论是α还是β,代表的都只是一方(这里我们取为本方)获胜的值)。
在这一情况下,如果我们对每一种可能出现的结果都进行评估,就会发现计算量很大。并且,并不是每一种情况都有可能出现;例如当本方知道如果做出这一选择,本方一定会输时,无论如何本方都不会做出这一选择。所以,为了简化计算,α、β剪枝法由此诞生。
α、β剪枝法
在搜索算法中优化中,剪枝,就是通过某种判断,避免一些不必要的计算。类比园丁,就是剪去了搜索树中的某些“枝条”,让其他的更有用的枝干能够更好地生长,故称剪枝。应用剪枝优化的核心问题是设计剪枝判断方法,即确定哪些枝条应当舍弃,哪些枝条应当保留的方法。在α、β剪枝法中,枝条被舍弃的条件就是——α>β。
这一条件并不是随便给出的,而是有博弈理论基础的。其实这一条件应该细分为两个:
1、当A(即本方)进行决策后,现在的α>原先的β,这种状况是B(即对方)不希望看到的,所以他会避免这种情况的发生,即不让A有做出这一选择的机会,即B会在自己前一轮的选择中避开这一情况出现的可能。所以我们不必考虑A所做出的这个选择即其下面的分支,这也叫做α剪枝。
2、当B进行决策后,原先的α>现在的β,这种状况是A不希望看到的(因为无论αβ都是A获胜的可能),即A会避免这种情况,不让B有可能做出这一决策,同理,不必考虑B所做出的这个选择即下面的分支,这也叫做β剪枝。
下面,我将用例子来进行说明。
首先,我们先自下而上来看
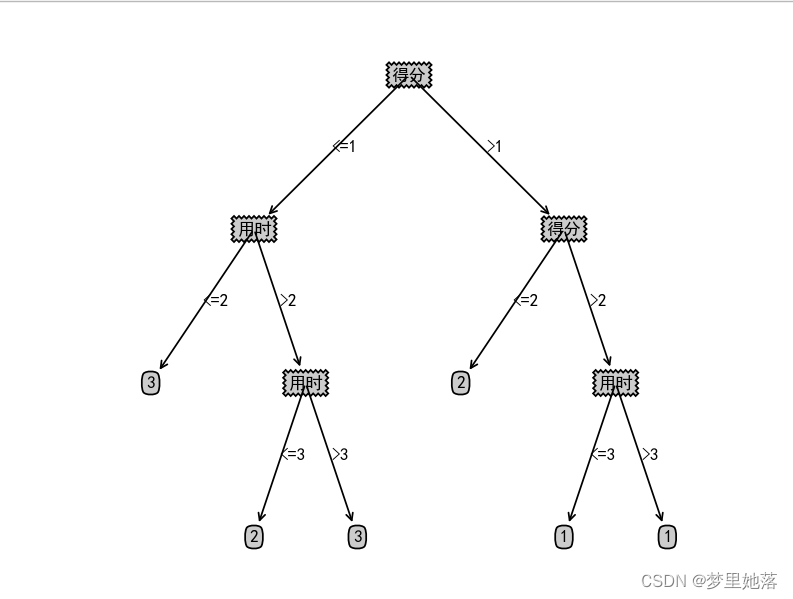
首先需要先明白几个点,第一层是伴随A进行第一次选择而开始的。矩形表示A的回合,圆形表示B的回合;同时,无论是A还是B,他们进行选择之后的值,将被写在下一次的框内。同时,我们定义,α的初始值为-∞,而β的初始值为+∞(我个人地理解是,互相把对手想得十分厉害,所以自己胜利的可能很小);换言之,为了实现自己利益最大化,A会尽量修改α的值,找到可能的最大值,而B则会修改β使之尽可能的小。

在第四层中,有1、5两种选择,对于B来说,他要使β值尽可能地小,所以他会对比1、5和+∞,比较之后,他当然会选择min值,即1,即此时β=1;也即目前第三层的⚪中的数值为1。
接着我们再来看A上一轮的选择,即从第二层到第三层。

如果A在第二层时选择了第二个方案,表面上α的值更大了,但是当A这样选择之后,B可以做出相应的选择,让β=-2,此时,α>β。而A不可能让这种情况发生,所以A不会在第二层时选择第三层的第二个方案,所以不用再考虑这一分支的其他可能情况了,出现了第一次剪枝。

既然我们已经看完了从第一层的第一种选择衍生出来的各种情况,接下来我们可以考虑第一层的另外一种选择,姑且称之为PLAN B。

在PLAN B 中,如果B在第二层选择了让β=2,那么将会出现A在第三层让α=4,此时α>β,是B所不希望看到的,所以B不可能在第二层进行这个选择,所以这一分支也可以不用考虑。

综上,α、β剪枝法之所以会规定在α>β时就抹去该分支及其下属的情况,是因为当这一不等式成立时,A、B两方总有一方是绝对失利的,因而他们会提早规避,从而不让这种情况发生,因而我们无需为不可能出现的情况而担忧。当然,你也可以从另外一个角度,即公共解的方面进行了解,因为篇幅以及个人能力有限的原因,在这里我就不做赘述了,感兴趣的朋友可以参考这篇文章。
这是我第一次接触算法,对这个算法的研究也花了好几天的时间,但其中难免还是有许多不足的地方;加之本人画图能力实在有限,有许多需要用图表示的都没办法很好地表达出来;希望能够得到大家的批评指正和包涵;也希望这篇文章能够帮助刚接触到这一算法而还有许多疑惑的朋友们。