本文始发于个人公众号:TechFlow,原创不易,求个关注
今天是高等数学专题的第13篇文章,我们来看看定积分究竟应该怎么计算。
定积分的实际意义
通过之前的文章,我们基本上熟悉了定积分这个概念和它的一些简单性质,今天终于到了正题,我们要试着来算一算这个积分了。
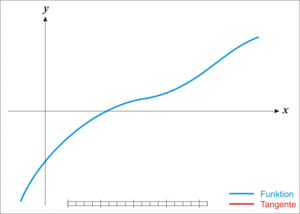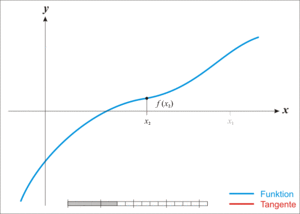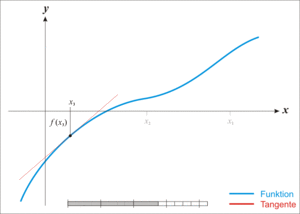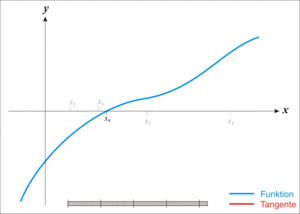
我们先来回忆一下对定积分的直观感受,它可以代表一段曲形面积,比如:

如果我们把上图当中的f(x)看成是速度函数,x轴看成是时间,那么f(x)就表示时刻x时物体运动的速度。那么我们把所有瞬时移动的距离累加,就得到了物体在某个时间段内的位移矢量,而这个位移长度恰好就是我们曲形的面积。我们把定积分和物理上的位移进行挂钩之后,很容易得出一个结论,在物理学上,一个物体发生的位移和时间也是一一映射的关系,所以这也是一个函数。
有了这个结论之后,我们就可以做一个假设,假设一个函数s(t)满足:
\[s(t) = \int_a^t f(t)dt
\]
计算推导
当我们把定积分和物理位移挂钩的时候,我们距离求解它已经很接近了。
根据物理上的定义,物体的运动速度其实就等于位置矢量随时间的变化率,虽然不够严谨,但其实这是一个微分量,可以近似看成是位移函数的导数。当然这个只是直观的认识,我们还需要用严谨的数学语言来表达。
我们假设f(x)函数在区间[a, b]上连续,并且\(\Phi(x) = \int_a^x f(t)dt, (a \leq x \leq b)\),我们试着证明\(\Phi'(x) = f(x)\)。
我们取一个绝对值足够小的\(\Delta x\),使得\(x + \Delta x \in (a, b)\),那么:
\[\Phi(x + \Delta x) = \int_a^{x+\Delta x}f(t)dt
\]
\[\begin{aligned}
\Delta \Phi &= \Phi(x+\Delta x) - \Phi(x) \\
&= \int_a^{x+\Delta x} f(t)dt - \int_a^x f(t)dt\\
&= \int_x^{x+\Delta x}f(t)dt
\end{aligned}
\]
\[\begin{aligned}
\Delta \Phi &= f(\xi) \Delta x\\
\frac{\Delta \Phi}{\Delta x} &= f(\xi)
\end{aligned}
\]
\[\Phi'(x) = f(x)
\]
为了避免引战,很多课本上都把它叫做牛顿-莱布尼茨公式,用两个人的名字共同命名。
牛顿-莱布尼茨公式
根据原函数的定义,从上面的结论当中我们可以得到\(\Phi(x)\)是函数\(f(x)\)在[a, b]上的一个原函数。我们假设F(x)也是f(x)的一个原函数,所以我们可以知道\(F(x) - \Phi(x) = C\),这里的C是一个常数。
令x = a,那么可以得到\(F(a) - \Phi(a) = C\),根据\(\Phi(x)\)的定义,我们可以知道\(\Phi(a) = 0\),所以\(F(a) = C\),并且\(\Phi(x) = \int_a^x f(t)dt\),代入可以得到:
\[\begin{aligned}
F(x) - \Phi(x) &= C\\
F(x) - \int_a^x f(t)dt &= F(a)\\
\int_a^x f(t)dt &= F(x) - F(a)
\end{aligned}
\]
我们回顾一下上面的推导过程,难度并不大,但是几个代换处理非常巧妙,不然的话即使我们可以得到结论,也并不严谨。
总结
有了定积分的计算公式之后,很多我们之前无法解决的问题就都可以解决了,由此奠定了整个微积分的基础,不仅推动了数学的发展,也带动了理工科几乎所有的学科。在各大理工学科之中几乎都有用到微积分进行一些复杂的计算,即使是看起来和数学不那么相关的计算机领域也不例外,这也是大学里为什么给所有理工科的学生开设了这门课的原因。
但遗憾的是,在我们学习的时候往往很难预见它的重要性,然而当我们预见这一点的时候,往往已经是很多年之后,没有那样的环境和时间给我们去好好学习了。
今天的文章就是这些,如果觉得有所收获,请顺手点个关注或者转发吧,你们的举手之劳对我来说很重要。

![[计算机数值分析]牛顿插值公式](https://img-blog.csdnimg.cn/8650057526d844c8a0371b30f005f4a0.png)