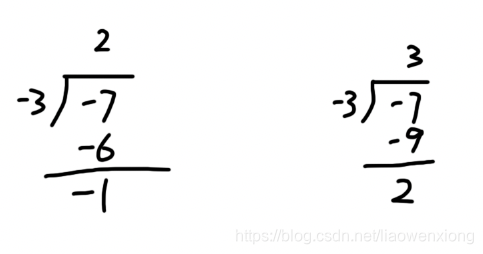目录
壹:科赫雪花曲线(Koch Snowflake Curve)
贰:想法(ideas)
叁:代码实现(Code Implementation)
肆:打包(Packing)
伍:附录(Appendix)
壹:科赫雪花曲线(Koch Snowflake Curve)
在正式开始本文的叙述前,我们需要先了解一些小知识——什么是“科赫雪花曲线”?
1904年,瑞典数学家冯·科赫(H·V·Koch)提出了科赫曲线的概念。因为科赫曲线的形状类似雪花,科赫曲线也被称为雪花曲线。
科赫曲线的绘制方法:
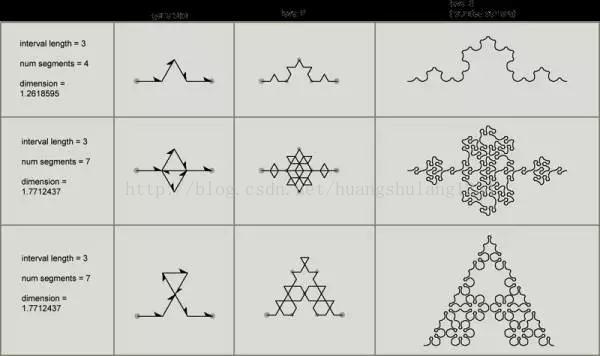
- 正整数“n”代表科赫曲线的阶数,表示生成科赫曲线过程的操作次数。
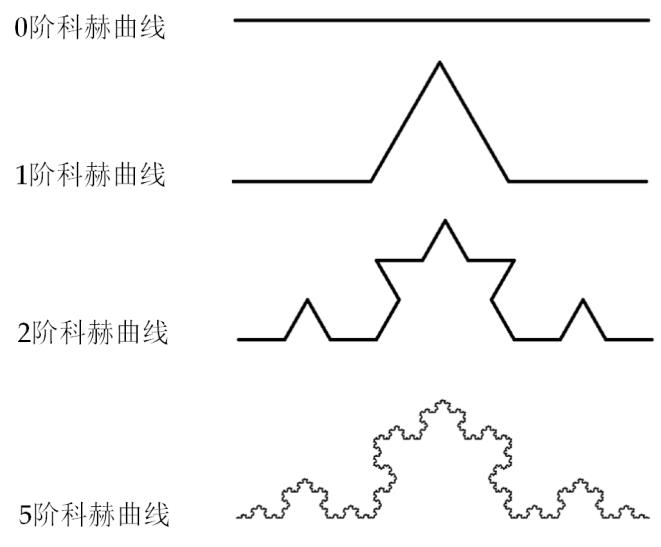
- 0阶科赫曲线,表示,一条长度为L的直线。
- 1阶科赫曲线:
- 首先,将长度为L的直线三等分;其次,将中间的一段用边长为L/3的等边三角形的另外两边代替;最后,1阶科赫曲线就是这样啦。
- 更高阶的科赫曲线以此类推(即,分别对已经等分的线段再进行等分)。
一阶科赫曲线:
二阶科赫曲线:
"Okay, so much. Time to go ahead!"
当"turtle库"与“科赫雪花曲线”相遇,会发生怎样的作用呢?更精美的图形!
科赫雪花曲线(5阶):

5阶的科赫雪花曲线很漂亮,对吧?但,怎么觉得哪里有问题呢?哈哈,我想你应该发现了,上图是一个组合图形(狗头.png)。它是我们用科赫曲线(5阶)替换了等边三角形的三条边得到的。
那,我们怎么绘制上图呢?
贰:想法(ideas)
我们要调用哪些函数库呢?嗯……让我想好好想。
既然要作图,那么"turtle库"是必须的;科赫雪花曲线的话,很有趣,我希望分享给朋友的".py"文件能够直接运行,那么……"pyinstaller库"!别的库,应该用不到了。
那么,我需要用到哪些知识点呢?
毋庸置疑的,关于"turtle库"的相关知识我要掌握;根据科赫曲线的定义,我们知道,绘图的过程是不断重复重复重复……的。那么我要用到"def"来帮我封装函数。“分别对已经等分的线段再进行等分”,是用到了“函数的递归”吗?
欸,“函数的递归”是什么意思来着?我查查。
(3000 years later……)
“函数的递归——我们在定义的函数中再次调用该函数。即,我调用了我自己。”当我们在使用函数的递归时,需要特别注意一点:基例的构建。不然,函数一直在调用自己调用自己……我们还怎么得到结果呢?
叁:代码实现(Code Implementation)
好啦,现在,让我们看一下怎么用代码来实现我们的思路吧~
我们应该怎么做呢?
# Created by Yuriko, all rights reserved!'''说明:壹:是,绘制“科赫雪花曲线”的,脚本。贰:函数“koch_curve(length,n)”中,“n”表示科赫曲线的阶数。且,“n”的取值为自然数。叁:推荐“n”,取值:[0,5]。'''#%%
# 调用函数库。import turtle as t#%%# 封装函数。def koch_curve(length,n):if n == 0:t.fd(length) # 基例。else:for x in [0,60,-120,60]:t.lt(x)koch_curve(length/3,n-1) # 递归,我调用了我自己。def draw_it():t.speed('fastest');t.color('lightblue')length = 300n = eval(input('需要绘制几阶的科赫雪花曲线?'))for x in range(3):koch_curve(length,n)t.rt(120)def main():t.setup(600,600)t.up(); t.goto(-150,100); t.down() # 调整画笔位置。draw_it() # 作图。t.hideturtle()t.done()#%%
# “F5”运行脚本。main()#%%
# To be continued.大功告成啦!好耶!!!
接下来,就让我们的搬家公司("pyinstaller库")将代码打包吧~
肆:打包(Packing)
以Anaconda环境为例:
首先,在开始菜单(Start Menu)找到“命令提示符”;然后,分别敲入下行代码。
Microsoft Windows [版本 10.0.19043.2006]
(c) Microsoft Corporation。保留所有权利。C:\Users\will>conda activate(base) C:\Users\will>activate violet(violet) C:\Users\will>D:(violet) D:\>pyinstaller -F Koch_Curve.py然后,我们去“dist”文件夹找到打包好了的“Koch_Curve.exe”文件。

运行ing……
“啊这,啊这,啊这——出现了什么问题呢?”
在冷静、思考、总结后,我们发现,问题出在“n = eval(input('需要绘制几阶的科赫雪花曲线?'))”。那好吧,我们还是内定“n”的值吧。
n = 5
# Created by Yuriko, all rights reserved!'''说明:壹:是,绘制“科赫雪花曲线”的,脚本。贰:函数“koch_curve(length,n)”中,“n”表示科赫曲线的阶数。且,“n”的取值为自然数。叁:推荐“n”,取值:[0,5]。'''#%%
# 调用函数库。import turtle as t#%%# 封装函数。def koch_curve(length,n):if n == 0:t.fd(length) # 基例。else:for x in [0,60,-120,60]:t.lt(x)koch_curve(length/3,n-1) # 递归,我调用了我自己。def draw_it():t.speed('fastest');t.color('lightblue')length = 300# n = eval(input('需要绘制几阶的科赫雪花曲线?'))n = 5for x in range(3):koch_curve(length,n)t.right(120)def main():t.setup(600,600)t.up(); t.goto(-150,100); t.down() # 调整画笔位置。draw_it() # 作图。t.hideturtle()t.done()#%%
# “F5”运行脚本。main()#%%
# To be continued.
# 一个建议,修改代码时,有时,“#”要比直接“Del”掉好。
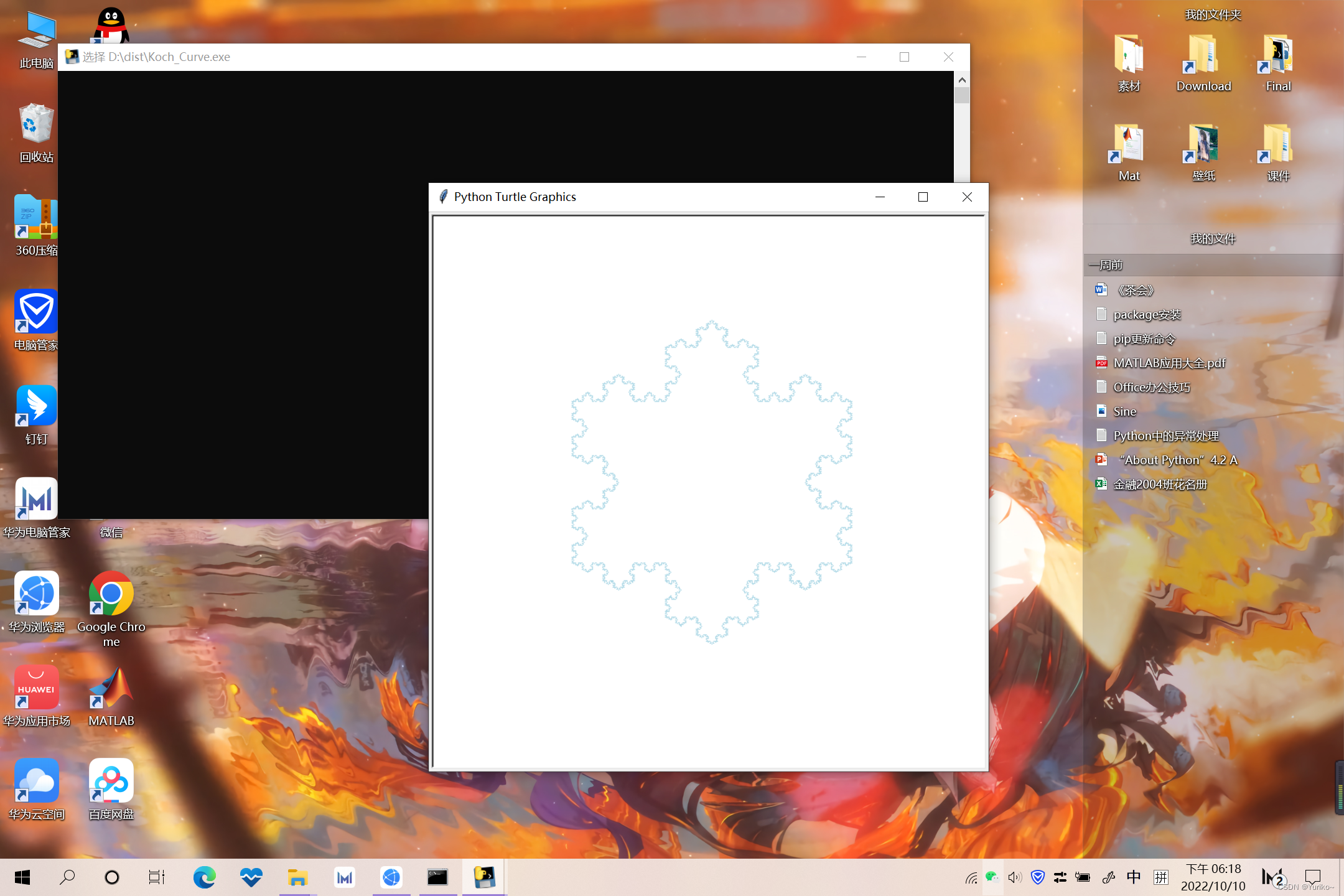
大成功!
伍:附录(Appendix)
不知道大家有没有遇到过这种情况:我们用"pyinstaller库"将代码文件打包好了,但是但是但是,运行“.exe”文件时,命令窗口一闪而过!灵异事件?!
嗯,关于这个问题的解决很简单。
#%%
# 调用函数库。import os#%%
# Body.'''你的代码的主体部分'''os.system('pause')#%%
# To be continued.你学会了吗?