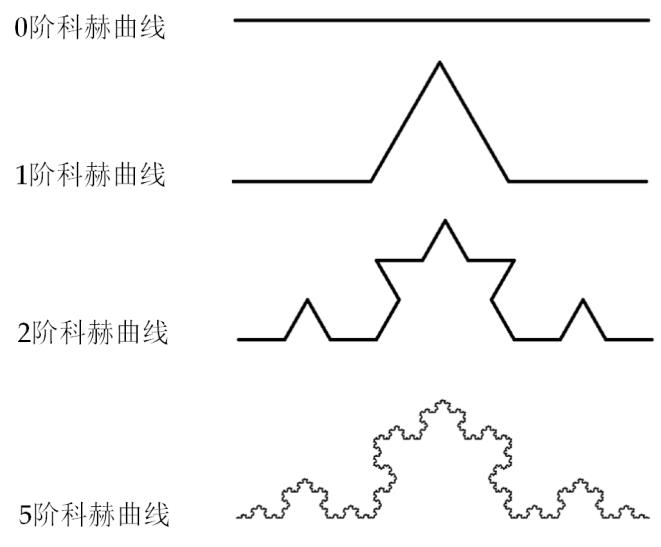
首先我们来绘制一个基本的3阶科赫雪花,由于和课上用的软件不一样,所以在课上看的代码只能当参考,实际比较繁琐。
代码如下
import turtle # 引入决解问题需要的工具——turtle作图包# 定义turtle画笔和画布的参数
def huabi(): turtle.speed(0) # speed()参数有[0,10]:“0”特殊、代表最快速度,其余[1,10]值越大、速度越快turtle.pensize(2) # 设置画笔宽度为2turtle.setup(800,800, 100, 10) # setup()参数有4个:前两个代表画布的“宽”和“高”,当数值为整数时、表示绝对像素大小,当小数时、表示站屏幕的比例。后两个可以省略,默认为屏幕中心位置,代表距离“屏幕左上角”的距离,单位是像素密度,turtle.penup() # 抬起画笔,之后的画笔动作、就不会产生图线turtle.goto(-300, 100) # 以画布中心点为坐标原点(0,0),将画笔移动到坐标(-300,100)处turtle.pendown() # 落下画笔,以便画图# 定义“尖”
def koch(size, n):if n==0: # 0阶的科赫雪花曲线就是一条线,大小为输入的“size”turtle.fd(size)else: # 高阶科赫雪花曲线for i in [0, 60, -120, 60]: # turtle在“尖”的四条线上改变的角度,分别为0°,60°,-129°,60°turtle.left(i) # 对应上边四个角度,一共需要转4次弯,画出本阶的四条线,koch(size/3, n-1) # 每个角度下的一个边,对应低一阶的客户雪花曲线的“尖”;至此完成函数本身的循环和复用,自动画出一个完整的n阶“尖”# 定义“边”
def sdkoch(size, n): # 完整的科赫雪花曲线由3个“边”组成,我们以上完成的是一个由“尖”组成的“边”,koch(size, n)turtle.right(120) # 2行代码一组,koch(size, n)turtle.right(120)koch(size, n) # 至此,得到完整的n阶科赫雪花曲线turtle.hideturtle() # 把turtle的光标隐藏turtle.done() # 结束turtle# 定义main()主函数
def main(size, n): # 设定参数接口huabi()sdkoch(size, n)main(500, 2) # 在设定参数之后,调用主函数import turtle
def koch(size, n):if n == 0:turtle.fd(size)else:for angle in [0, 60, -120, 60]:turtle.left(angle)koch(size/3, n-1)
def main():turtle.setup(600, 600)turtle.penup()turtle.goto(-200,100)turtle.pendown()turtle.pensize(2)level = 3 #三阶的科赫曲线koch(400, level) turtle.right(120) #转动120度,使得科赫曲线能围城一个三角形,形成最终的科赫雪花koch(400, level)turtle.right(120)koch(400, level)turtle.hideturtle() #隐藏画笔
main()
效果如下

接下来我们可以动用自己的创意来改进,可惜我失败了最后参考了许多大佬的代码和讲解,copy了这份代码
如下
import turtle
import timedef koch(size, n): # 定义弯曲的直线使其有棱角if n == 0:turtle.fd(size)else:for angle in [0, 60, -120, 60]: # 每一次都对其进行合理的角度改变turtle.left(angle)koch(size / 3, n - 1)def main(n):global aglobal sif a == 1:turtle.color("black") # 这边是控制画笔的颜色elif a == 2:turtle.color("purple")elif a == 3:turtle.color("blue")elif a == 4:turtle.color("Cyan")elif a == 5:turtle.color("green")elif a == 6:turtle.color("yellow")elif a == 7:turtle.color("orange")elif a == 8:turtle.color("red")if n != 0:a += 1turtle.penup()turtle.goto(-200 * (4 / 7) ** (s - n), 100 * (4 / 7) ** (s - n))# 每一次都是需要合理的等比例的扩大或是缩小turtle.pendown()turtle.pensize(2)level = 5koch(400 * (4 / 7) ** (s - n), level) # 大小是一个一个试出来的# 不能超过setup的设定的范围 600,不然就越界了turtle.right(120)koch(400 * (4 / 7) ** (s - n), level)turtle.right(120)koch(400 * (4 / 7) ** (s - n), level) # 注意这里koch一次就要转一次角度turtle.right(120)turtle.hideturtle() # 隐藏画笔main(n - 1)a=1
s = int(input()) # 输入其中的科赫曲线的个数
turtle.setup(600, 600)
turtle.speed(0)
main(s) # main(8)效果如下

但是此代码绘制时间过于缓慢,本人需求广大网友指点迷津。