作者:Milo Yip
链接:https://zhuanlan.zhihu.com/p/24688522
1. 科赫雪花和科赫曲线
科赫曲线(Koch curve)是一个简单的分形(fractal)图形。瑞典数学家海里格·冯·科赫(Helge von Koch:https://en.wikipedia.org/wiki/Helge_von_Koch)于 1904 年的论文 [1] 中提及科赫曲线的构造方法。
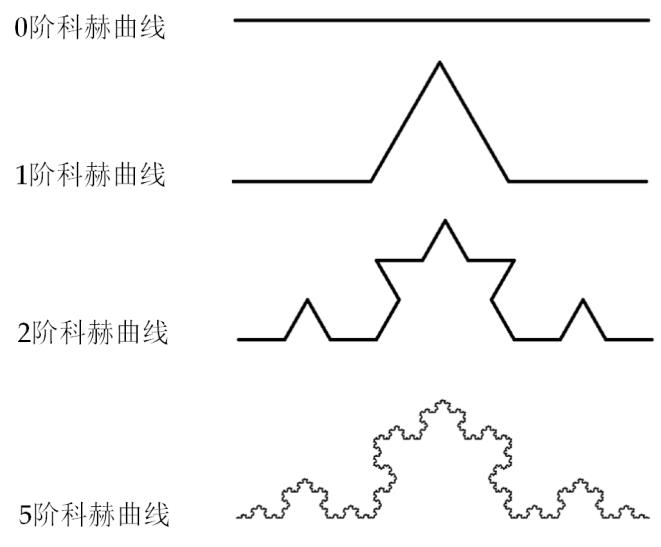
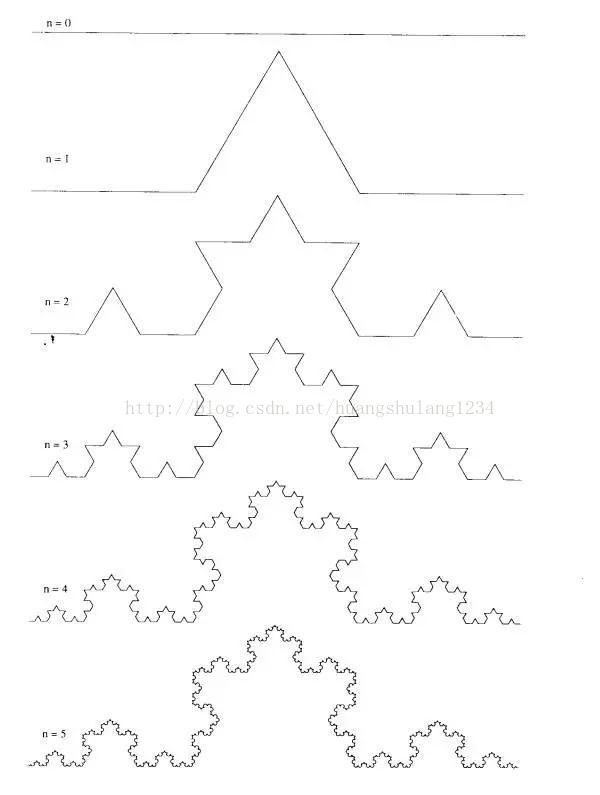
给定一直线线段,把它等分三段,加入一个等边三角形,以三段的中间一段为底对齐,再去除该段线段。然后,对每个新线段重复进行上述步骤,就能形成科赫曲线:
 当
当

,科赫曲线的长度也是无穷的。
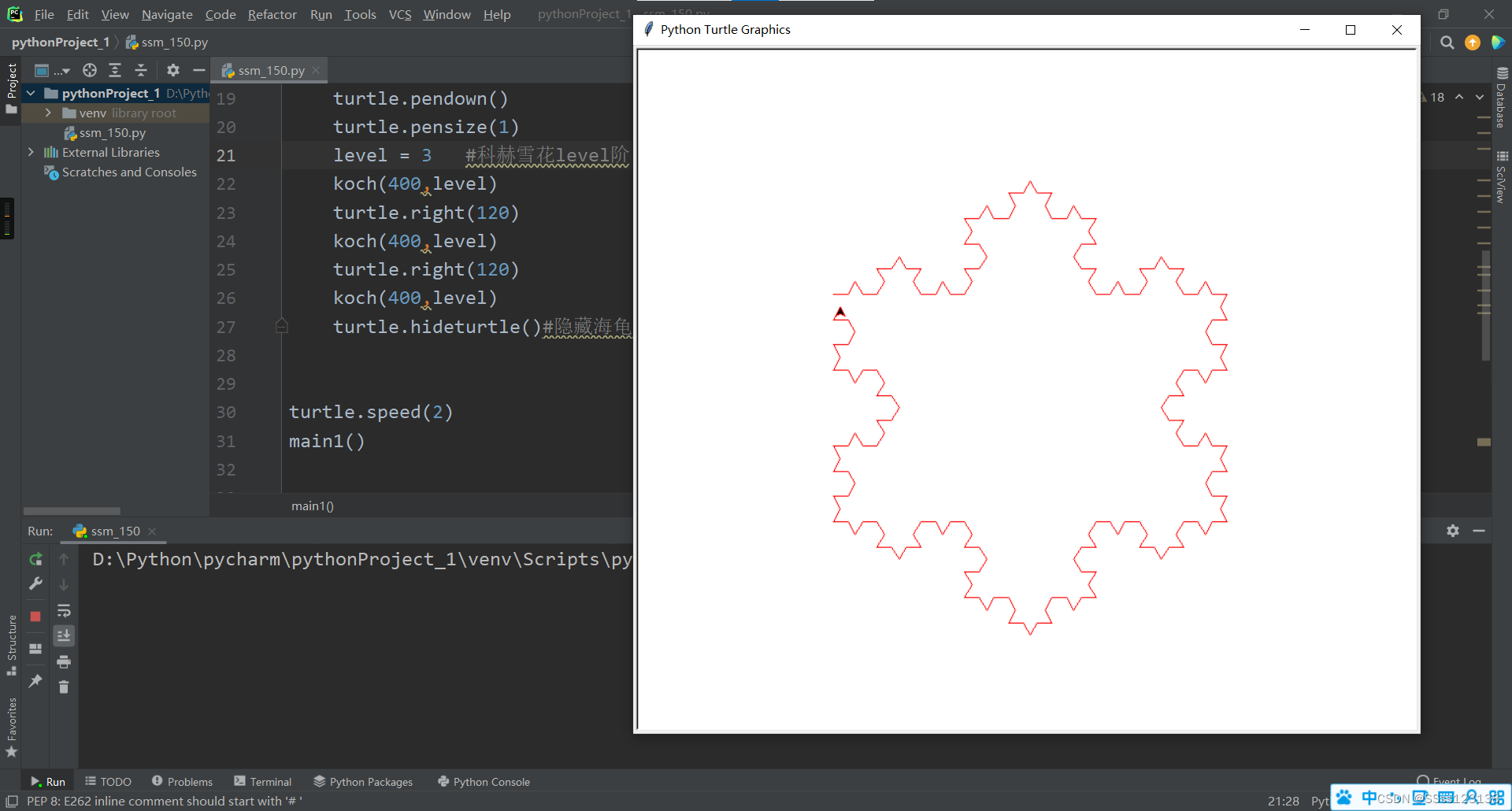
如果画 3 条科赫曲线,每次旋转 120 度,就能得到科赫雪花(Koch snowflake:https://en.wikipedia.org/wiki/Koch_snowflake):

2. 用 ASCII 字符绘画
我们可以用斜线 /、反斜线 \、下划线 _ 和空格这 4 个 ASCII 字符来绘画这个图形:
n=0
__
n=1
__/\__
n=2
__/\__
\ /
__/\__/ \__/\__
但有些情况我们需要在一个字符中画下划线和斜线,例如 n = 3 的时候:
n=3
__/\__
\ /
__/\__/ \__/\__
\ /
这里 -> /_ _\
这时候我们可以选择只画斜线、反斜线。
3. 用 C 语言实现科赫曲线
我们创建一个字符数组 image 作为画布,用于存储绘画的中间结果,最后再把数组打印出来。数组的大小为画布宽长之积 w * h。
设坐标系统是 x 向右、y 向下,并定义字符的左下角为坐标。例如,画笔从 (x, y) 之处往右画,便赋值 image[y * w + x] = '_' ,并把 x 增 1。
我们也定义 6 个方向,0 代表向右,1代表右上,2 代表左上等。注意水平方向(0 和 3)需要画两个下划线,其他方向只画一个字符。
每次调用 KochCurve(n, dir) 函数,表示我们要从当前位置 (x, y) 向 dir 方向绘画一条 n 阶科赫曲线。那么要画一条 n 阶科赫曲线,其实就只需要根据所需方向画 4 条 n - 1 阶科赫曲线。直到 n = 0,一条 0 阶科赫曲线就是一条直线,我们届时只需按 dir 用字符画一条直线。
完整代码如下:
#include #include static char* image;static int x, y, w, h;static void Put(int i, int j, char c) {
char *p = image + j * w + i;
if (*p == ' ' || *p == '_') // _ can be overridden by / or \.
*p = c;}static void KochCurve(int n, int dir) {
if (n == 0)
switch (dir % 6) {
case 0: Put(x++, y , '_' );
Put(x++, y, '_' ); break;
case 1: Put(x++, y--, '/' ); break;
case 2: Put(--x, y--, '\\'); break;
case 3: Put(--x, y, '_' );
Put(--x, y, '_' ); break;
case 4: Put(--x, ++y, '/' ); break;
case 5: Put(x++, ++y, '\\'); break;
}
else {
KochCurve(n - 1, dir );
KochCurve(n - 1, dir + 1);
KochCurve(n - 1, dir + 5);
KochCurve(n - 1, dir );
}}int main() {
w = 2;
h = 1;
for (int n = 0; n < 4; n++) {
char b[w * h];
image = b;
memset(image, ' ', w * h);
x = 0;
y = h - 1;
KochCurve(n, 0);
printf("\nn=%d\n\n", n);
for (int j = 0; j < h; j++) {
for (int i = 0; i < w; i++)
putchar(image[j * w + i]);
putchar('\n');
}
w *= 3;
h = n == 0 ? 1 : h * 3;
}}
main() 中使用了 C99 的 VLA 分配 image 数组,如用 C89 可改为 malloc()/free()。
4. 实现科赫雪花
科赫雪花仅仅是由 3 科赫曲线组成。我们只需改一下 main(),把画布变大一点,以及在合适的起始坐标画 3 条科赫曲线:
int main() {
w = 2;
h = 4;
for (int n = 0; n < 4; n++) {
char b[w * h];
image = b;
memset(image, ' ', w * h);
x = 0;
y = h / 4 - 1;
KochCurve(n, 0);
KochCurve(n, 4);
KochCurve(n, 2);
printf("\nn=%d\n\n", n);
for (int j = 0; j < h; j++) {
for (int i = 0; i < w; i++)
putchar(image[j * w + i]);
putchar('\n');
}
w *= 3;
h = n == 0 ? 4 : h * 3;
}}
输出(只展示 n = 3):

5. 总结与扩展
分形图形可以用极简单的定义,生成复杂的图形。在本文中,展示如何用 C 语言中,利用递归和 ASCII 字符绘画出科赫曲线和科赫雪花。
你还可以简单地改变 KochCurve() 中的实现,产生不同的变种,如The Root 9 Triangle Grid Family展示的:
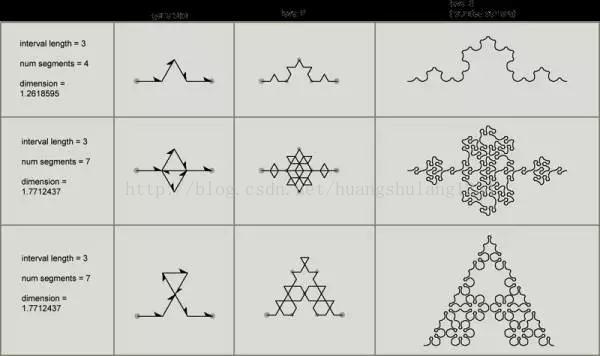
你还可以尝试一下,不使用画布,而是用《如何用 C 语言画这个图:https://zhuanlan.zhihu.com/p/23692828》的框架来绘画,但这样需要在每个字符格子绘画整条曲线,性能较差。要提升性能,可使用每阶科赫曲线的包围盒( bounding box)作剔除──如果现时的坐标不在包围盒之内,也毋须递归到低一阶的科赫曲线了。
参考
[1] Von Koch, Helge. "Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire."Arkiv för Matematik1 (1904): 681-704.
版权申明:内容来源网络,版权归原创者所有。除非无法确认,我们都会标明作者及出处,如有侵权烦请告知,我们会立即删除并表示歉意。谢谢。
-END-