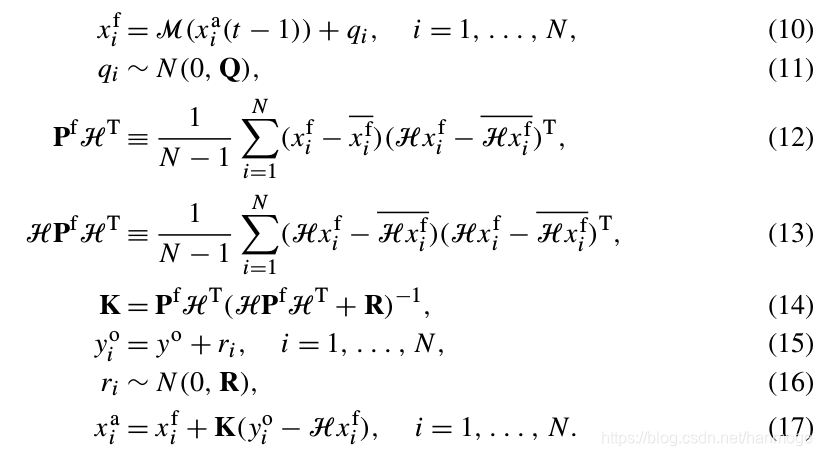卡尔曼滤波（Kalman filter）及预测

article/2025/10/5 19:40:01

参考文章：https://blog.csdn.net/baidu_38172402/article/details/82289998; https://www.jianshu.com/p/2768642e3abf

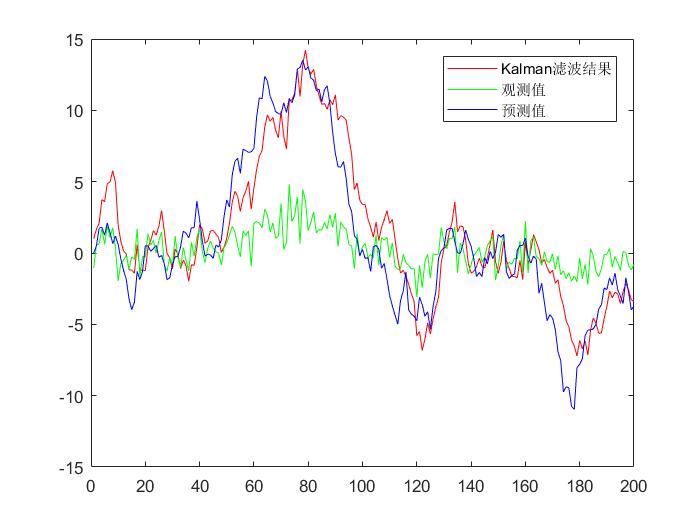
kalman滤波的作用：1.数据滤波；2.数据预测 3.数据融合。其基本原理：是通过协方差来进行加权。

1.什么是Kalman

A Linear Dynamical System is a partially observed stochastic process with linear dynamics and linear observations, both subject to Gaussian noise. It can be defined as follows, where X(t) is the hidden state at time t, and Y(t) is the observation.

   x(t+1) = F*x(t) + w(t),  w ~ N(0, Q),  x(0) ~ N(X(0), V(0))y(t)   = H*x(t) + v(t),  v ~ N(0, R)

The Kalman filter is an algorithm for performing filtering on this model, i.e., computing P(X(t) | Y(1), ..., Y(t)).
The Rauch-Tung-Striebel (RTS) algorithm performs fixed-interval offline smoothing, i.e., computing P(X(t) | Y(1), ..., Y(T)), for t <= T.

噪声（不确定性）来源： 1.本身的高斯噪声 2. 观测存在的噪声。

其优势在于：它的优点是在预测时并不需要记录很多系统过去的状态，只需要知道上一状态的预测结果的误差协方差矩阵就可以了，所以kf可以算得很快，可以用于实时的动态系统。迭代

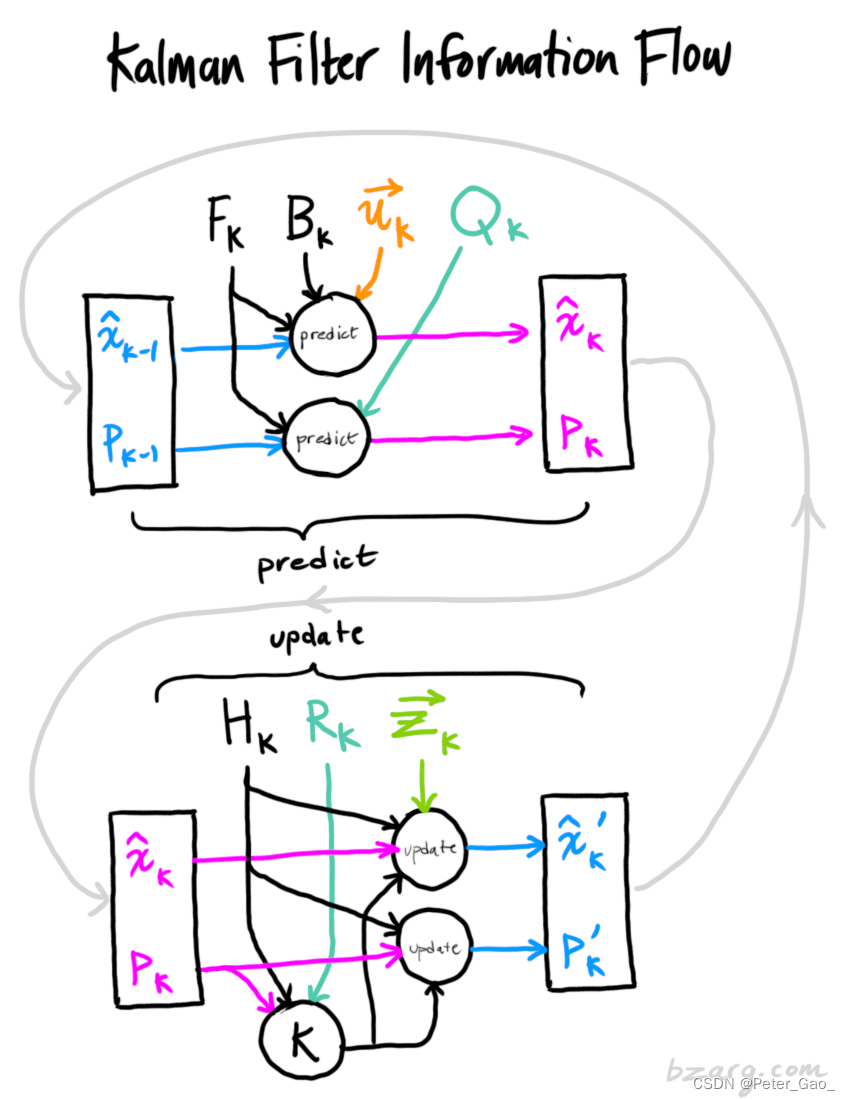
状态方程（即怎么从x(k-1)更新到x(k)）:

状态方程之后，就是协方差了。初始协方差矩阵=【1 0；0 1】，后面根据协方差矩阵性质与状态空间矩阵，更新了协方差矩阵。

但是这个状态方程只是一个很基础的，我们还需要考虑其他因素对系统的影响，比如说电机对机器人的控制，外界干扰等等。

我们首先考虑电机对机器人的控制，如果加上电机的加速度，则空间状态方程为：

Bk就是控制矩阵，uk就是加速度向量。

此外还要考虑噪声的影响，如果加上噪声，则每一个（k－1）时的点不会对应到K时的一个点，而是对应到一片区域，所以对应关系如下：

因为每一个点都对应到一片区域，所有的对应叠加在一起，得到的新的K的分布范围应该比以前要大，如下图所示：

面积明显比上图要大，同时我们假设噪声是高斯白噪声，所以期望为0，所以加上噪声后K的期望不变。假设噪声所造成的那个小绿圈的速度与位置的协方差矩阵为Qk，则新的主观预测和协方差矩阵为：

通过这个方程我们可以在X（k－1）时主观的预测出Xk时的状态。下一步就是得到客观测量的结果。

【分析：Fk根据内在联系，速度与位置的关系，可以得出状态空间方程，Bk也是，Pk开始设立初始值，后续更新。Qk为噪音矩阵如何求取呢？可以设一个固定值Q = 0.1*eye(2)=0.1*【1 0；0 1】】】

到这里，预测就完成了。

example【参考：2】:

z=[0.39	0.50	0.48	0.29	0.25	0.32	0.34	0.48	0.41	0.45]
%% 初始参数设定
ss = 1; % state size  状态矩阵只有角度,矩阵为[1]
os = 1; % observation size  观察矩阵也是如此
%Q=[0.001]  %观测噪音矩阵
P=[1]; 
A=[1]  %状态矩阵
xbar=A*z(1);
R=0.01*[1];
H=[1]  %Z=H*xk+vk，H为测量值与真实值的映射矩阵
xbar(1)=0;
Pbar(1)=1;
x(1)=z(1);    for t=2:length(z)%预测Pbar(t)=A*P(t-1)*A';   %对于协方差来说，我们认为观测协方差（方差）是稳定的，R=0.1，但是预测的协方差在改变xbar(t)=A* x(t-1);%引入测量值滤波%K(t)=Pbar(t)*H'*inv(H*Pbar(t)*H'+R);K(t)=(Pbar(t)*H')/(H*Pbar(t)*H'+R);x(t)=xbar(t)+K(t)*(z(t)-H*xbar(t));P(t)=(1-K(t)*H)*Pbar(t);
end
plot(xbar,'r')
hold on 
plot(x,'b--')
plot(z,'y*')
hold off
legend('预测值xbar','滤波值x','观测值z')

2.预测

在很多场景，比如角度传感器。人们往往希望驱动机构到某个位置，即存在提前预测，并以预测的数据作为控制依据。

滤波后的这个最优预测并不是用于实际的使用，实际中还是使用主观预测部分为估计，但是当到下一个时间点得到客观测量后，我们可以修正我们的估计，得到最优估计，这个估计是作为参数传递给下一次估计，这样一次次修正，我们的估计会更加精确。

简而言之，假如你要提前预测值控制，你可以先用着，这不是最好的值。后面可以滤波更新，迭代下去。

许多场景下，我们试图预测更长步数，但是预测主要是基于模型，比如温度，我们预测t2=t1，即短时间内，温度变化不大，既然是基于模型，那么预测的准确度就不大。

与三次指数平滑预测相比，三次指数平滑其基于其数据特征（趋势，周期性），其最简单的预测是y=kx+b线性预测。可以预测多步。

据此，我们认为kalman滤波不适宜多步预测，尤其在预测模型不足够准确的情况下（期待讨论）。

3. 数据融合

下面我们考虑多个变量的情况，这时数据的波动情况就不能用方差表示了，应该用协方差矩阵来表示，所以直接替换得到的新的分布和新的K：

这样，我们就得到多变量时的Kalman Gain。这个分布期望就是我们最终的预测。协方差矩阵就是我们要传给下一次预测的信息。

资源下载：

【1】.kalman matlab工具箱：https://blog.csdn.net/congduan/article/details/8163407；这个工具箱 supports filtering, smoothing and parameter estimation (using EM) for Linear Dynamical Systems.

【2】.一维数据kalman滤波的例子，http://bilgin.esme.org/BitsAndBytes/KalmanFilterforDummies