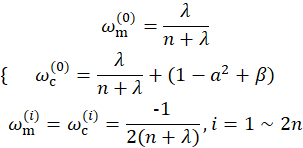此篇为第⑤篇，多目标跟踪系列文章：
基础demor入门①②；公式推导③④；深入分析初始化参数的影响⑤；
① Matlab Kalman滤波例子——小球跟踪解析 ：matlab官方例子，单目标跟踪。匀速模型和匀加速模型
②Matlab Kalman Filter based Multiple object Tracking 官方例子 多目标跟踪_hello world-CSDN博客matlab官方例子，多目标跟踪。注意有匈牙利轨迹分配算法，且其中的距离计算公式为观测与预测的马氏距离，这个来源于1987年的作者的著作中。 
③kalman滤波——公式推导_hello world-CSDN博客_卡尔曼滤波递推公式
理解马氏距离的公式！ 理解残差和残差协方差！
④多目标跟踪——阶段性进展_hello world-CSDN博客_多目标跟踪 多目标综述、Kalman滤波公式推导
⑤kalman简单例子——初始化参数对kalman性能的影响_hello world-CSDN博客
⑥多目标跟踪中的目标是否静止判断_hello world-CSDN博客 判断是否静止，如何计算速度
CheckStatic代码原理解析，数学公式推导。
其它优秀的博客参考：
⑦多目标跟踪（MOT）入门 - 知乎 比较好的多目标MOT综述！
⑧《Towards Real-Time Multi-Object Tracking》论文翻译 - 知乎
⑨ 视频轨迹跟踪分析——他山之石_hello world-CSDN博客

---

一、简单功能实现 

一维信号的，匀速运动，位移预测。有观测Yn+1(S)。状态为Posx和vx。有过程噪声Vn，观测噪声Wn。具体数学模型如下： 

代码来源：卡尔曼滤波_周先森爱吃素的博客-CSDN博客_卡尔曼滤波的步骤

  注意：第34行和第35行的代码区别。34行为矩阵点乘，不是矩阵乘法。

 第一个为点乘，第二个为矩阵乘法。

    # p_predict = f * p * f.T + qp_predict = (f.dot(p)).dot(f.T) + q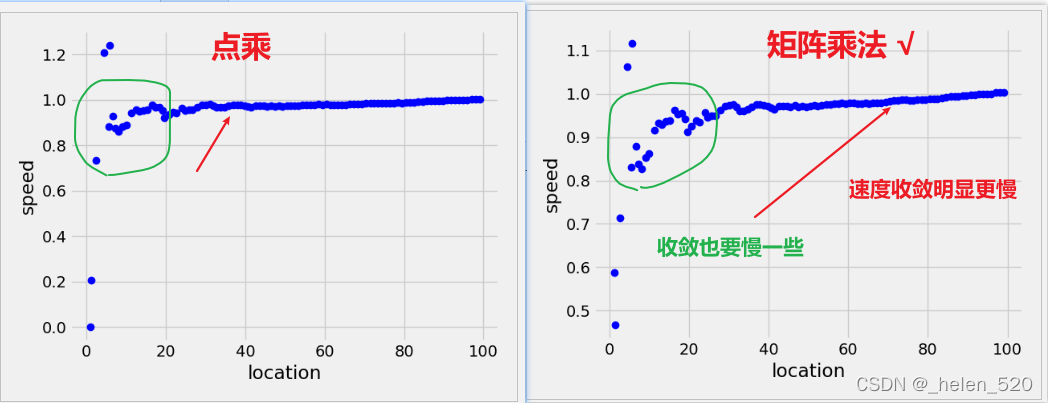

1.1 代码如下：

"""
Author: Zhou Chen
Date: 2020/3/27
Desc: 使用卡尔曼滤波进行状态预测
"""import numpy as np
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')# 创建位置观测矩阵，表示0-99的位移
z_observed = np.arange(100)
# 创建高斯噪声矩阵np.random.seed(0)
z_noise = np.random.normal(0, 1, 100)
z = z_observed + z_noise
# 创建初始状态矩阵Xn|n
x = np.array([[0, ], [0, ]])
# 创建初始状态协方差矩阵P，这里的1也可以是一个较为合适的较大数字 Pn|n
p = np.array([[1, 0], [0, 1]])
# 创建状态转移矩阵，采样频率为1秒，所以△t为1 Fn transition
f = np.array([[1, 1], [0, 1]])
# 创建状态转移协方差矩阵，协方差较小  Qn
q = np.array([[1e-6, 0], [0, 1e-6]])
# 创建观测矩阵 Hn
h = np.mat([1, 0])
# 创建观测噪声的协方差矩阵 Rn
r = np.mat([1])for i in range(100):# 迭代，计算5大步骤x_predict = f * x# p_predict = f * p * f.T + qp_predict = (f.dot(p)).dot(f.T) + qkalman = (p_predict * h.T) / (h * p_predict * h.T + r)x = x_predict + kalman * (z[i] - h * x_predict)p = (np.eye(2) - kalman * h) * p_predictplt.plot(x[0, 0], x[1, 0], 'bo')plt.xlabel("location")
plt.ylabel("speed")
plt.savefig("rst.png")
plt.show()

二、残差分析

此处的：X=（posx, Vx）一维情况，x的位置，x方向的速度。

观测 vx=1. Yn+1 = x + vx * Δt + noise
状态 X=(posx, vx)
初始化：Pn|n, Xn|n，Hn, Fn, Qn=1e-6, Rn=1 

 从上图可以看出：
① kalman校正的（蓝色点）更加接近真实值。这也是观测越来越权重小的表现
②观测Yn+1(绿色点) 由于观测误差Rn=1，值太大了。所以观测误差较大
③速度的估计情况（红色点）速度的估计误差要远小于位移的估计