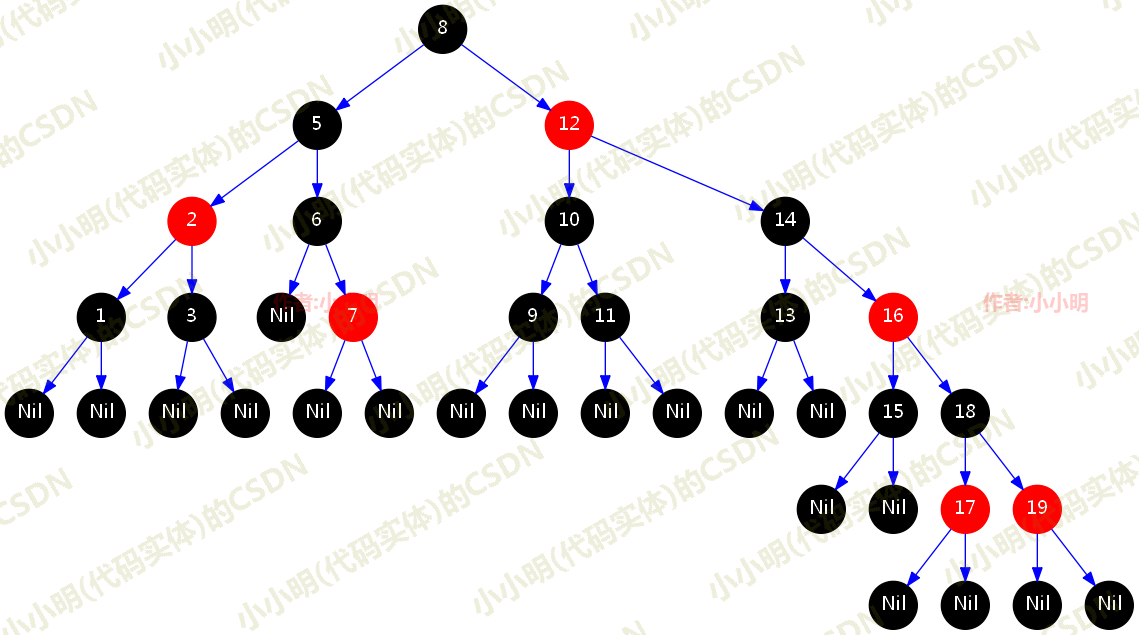
随处可见的红黑树

article/2025/5/15 6:33:51

随处可见的红黑树

    • 红黑树为什么常用
    • 那么红黑树怎么实现?
      • 红黑树的定义
    • 红黑树节点旋转
    • 红黑树的添加问题

红黑树为什么常用

1.当做查找以key-value
通过key去查找value,查找性能比较快
比如通过socket去查找客户端id,还有内核内存怎么使用?每用malloc分配一个内存就加入一颗红黑树,free(ptr)释放的时候key-value去查找对应的块
2.通过中序遍历是顺序的
进程的调度与红黑树什么关系呢?有些进程由于需要满足某些条件而处于等待状态等待某一个时间在未来某个时刻会再次运行,就把这些等待的再未来某个时刻会再次运行的进程加入红黑树去管理,
在这里插入图片描述

那么红黑树怎么实现?

那就不得不先聊二叉排序树了,名义上是二叉树,但是二叉树有一种最坏的情况是链表,违背了快速查找,为了更好的解决这个问题就引入了红黑树

在这里插入图片描述

二叉树的定义与实现

#include <stdio.h>
#include <stdlib.h>
#include <string.h>#include <assert.h>#if 0typedef int KEY_VALUE;struct bstree_node {KEY_VALUE data;struct bstree_node *left;struct bstree_node *right;
};struct bstree {struct bstree_node *root;
};struct bstree_node *bstree_create_node(KEY_VALUE key) {struct bstree_node *node = (struct bstree_node*)malloc(sizeof(struct bstree_node));if (node == NULL) {assert(0);}node->data = key;node->left = node->right = NULL;return node;
}int bstree_insert(struct bstree *T, int key) {assert(T != NULL);if (T->root == NULL) {T->root = bstree_create_node(key);return 0;}struct bstree_node *node = T->root;struct bstree_node *tmp = T->root;while (node != NULL) {tmp = node;if (key < node->data) {node = node->left;} else {node = node->right;}}if (key < tmp->data) {tmp->left = bstree_create_node(key);} else {tmp->right = bstree_create_node(key);}return 0;
}int bstree_traversal(struct bstree_node *node) {if (node == NULL) return 0;bstree_traversal(node->left);printf("%4d ", node->data);bstree_traversal(node->right);
}#define ARRAY_LENGTH		20
int main() {int keyArray[ARRAY_LENGTH] = {24,25,13,35,23, 26,67,47,38,98, 20,13,17,49,12, 21,9,18,14,15};struct bstree T = {0};int i = 0;for (i = 0;i < ARRAY_LENGTH;i ++) {bstree_insert(&T, keyArray[i]);}bstree_traversal(T.root);printf("\n");
}#elsetypedef int KEY_VALUE;#define BSTREE_ENTRY(name, type) 	\struct name {					\struct type *left;			\struct type *right;			\}struct bstree_node {KEY_VALUE data;BSTREE_ENTRY(, bstree_node) bst;
};struct bstree {struct bstree_node *root;
};struct bstree_node *bstree_create_node(KEY_VALUE key) {struct bstree_node *node = (struct bstree_node*)malloc(sizeof(struct bstree_node));if (node == NULL) {assert(0);}node->data = key;node->bst.left = node->bst.right = NULL;return node;
}int bstree_insert(struct bstree *T, int key) {assert(T != NULL);if (T->root == NULL) {T->root = bstree_create_node(key);return 0;}struct bstree_node *node = T->root;struct bstree_node *tmp = T->root;while (node != NULL) {tmp = node;if (key < node->data) {node = node->bst.left;} else {node = node->bst.right;}}if (key < tmp->data) {tmp->bst.left = bstree_create_node(key);} else {tmp->bst.right = bstree_create_node(key);}return 0;
}int bstree_traversal(struct bstree_node *node) {if (node == NULL) return 0;bstree_traversal(node->bst.left);printf("%4d ", node->data);bstree_traversal(node->bst.right);
}#define ARRAY_LENGTH		20
int main() {int keyArray[ARRAY_LENGTH] = {24,25,13,35,23, 26,67,47,38,98, 20,13,17,49,12, 21,9,18,14,15};struct bstree T = {0};int i = 0;for (i = 0;i < ARRAY_LENGTH;i ++) {bstree_insert(&T, keyArray[i]);}bstree_traversal(T.root);printf("\n");
}#endif

业务与数据结构混合在一起,同样的这套树能不能在不同的业务,比如进程的各种状态,就是这棵树的左右子节点不一样
1.如何创建
void* value ps:没有问题,还是需要再次寻址找内存,往往是这个value不知道是什么的时候写它,不管你定义什么把值直接往里面放,考虑到进程可有不同状态树就按这个技巧可以落在不同的树上结果,宏有美观作用;
malloc 红黑树内存分配如何组织起来,看到这个malloc应该就能想到在虚拟内存堆上面分配一块内存把它加入操作系统的内核,红黑树就是在这个基础上的一个变种;

红黑树的定义

在这里插入图片描述

定义怎么来的?可以有数学归纳法去证明
与二叉树这里还有不同之处是定义多一个nil,所有的叶子节点都指向这个nil

在这里插入图片描述

#include <stdio.h>
#include <stdlib.h>
#include <string.h>#define RED				1
#define BLACK 			2typedef int KEY_TYPE;typedef struct _rbtree_node {unsigned char color;struct _rbtree_node *right;struct _rbtree_node *left;struct _rbtree_node *parent;KEY_TYPE key;void *value;
} rbtree_node;typedef struct _rbtree {rbtree_node *root;rbtree_node *nil;
} rbtree;rbtree_node *rbtree_mini(rbtree *T, rbtree_node *x) {while (x->left != T->nil) {x = x->left;}return x;
}rbtree_node *rbtree_maxi(rbtree *T, rbtree_node *x) {while (x->right != T->nil) {x = x->right;}return x;
}rbtree_node *rbtree_successor(rbtree *T, rbtree_node *x) {rbtree_node *y = x->parent;if (x->right != T->nil) {return rbtree_mini(T, x->right);}while ((y != T->nil) && (x == y->right)) {x = y;y = y->parent;}return y;
}void rbtree_left_rotate(rbtree *T, rbtree_node *x) {rbtree_node *y = x->right;  // x  --> y  ,  y --> x,   right --> left,  left --> rightx->right = y->left; //1 1if (y->left != T->nil) { //1 2y->left->parent = x;}y->parent = x->parent; //1 3if (x->parent == T->nil) { //1 4T->root = y;} else if (x == x->parent->left) {x->parent->left = y;} else {x->parent->right = y;}y->left = x; //1 5x->parent = y; //1 6
}void rbtree_right_rotate(rbtree *T, rbtree_node *y) {rbtree_node *x = y->left;y->left = x->right;if (x->right != T->nil) {x->right->parent = y;}x->parent = y->parent;if (y->parent == T->nil) {T->root = x;} else if (y == y->parent->right) {y->parent->right = x;} else {y->parent->left = x;}x->right = y;y->parent = x;
}void rbtree_insert_fixup(rbtree *T, rbtree_node *z) {while (z->parent->color == RED) { //z ---> REDif (z->parent == z->parent->parent->left) {rbtree_node *y = z->parent->parent->right;if (y->color == RED) {z->parent->color = BLACK;y->color = BLACK;z->parent->parent->color = RED;z = z->parent->parent; //z --> RED} else {if (z == z->parent->right) {z = z->parent;rbtree_left_rotate(T, z);}z->parent->color = BLACK;z->parent->parent->color = RED;rbtree_right_rotate(T, z->parent->parent);}}else {rbtree_node *y = z->parent->parent->left;if (y->color == RED) {z->parent->color = BLACK;y->color = BLACK;z->parent->parent->color = RED;z = z->parent->parent; //z --> RED} else {if (z == z->parent->left) {z = z->parent;rbtree_right_rotate(T, z);}z->parent->color = BLACK;z->parent->parent->color = RED;rbtree_left_rotate(T, z->parent->parent);}}}T->root->color = BLACK;
}void rbtree_insert(rbtree *T, rbtree_node *z) {rbtree_node *y = T->nil;rbtree_node *x = T->root;while (x != T->nil) {y = x;if (z->key < x->key) {x = x->left;} else if (z->key > x->key) {x = x->right;} else { //Existreturn ;}}z->parent = y;if (y == T->nil) {T->root = z;} else if (z->key < y->key) {y->left = z;} else {y->right = z;}z->left = T->nil;z->right = T->nil;z->color = RED;rbtree_insert_fixup(T, z);
}void rbtree_delete_fixup(rbtree *T, rbtree_node *x) {while ((x != T->root) && (x->color == BLACK)) {if (x == x->parent->left) {rbtree_node *w= x->parent->right;if (w->color == RED) {w->color = BLACK;x->parent->color = RED;rbtree_left_rotate(T, x->parent);w = x->parent->right;}if ((w->left->color == BLACK) && (w->right->color == BLACK)) {w->color = RED;x = x->parent;} else {if (w->right->color == BLACK) {w->left->color = BLACK;w->color = RED;rbtree_right_rotate(T, w);w = x->parent->right;}w->color = x->parent->color;x->parent->color = BLACK;w->right->color = BLACK;rbtree_left_rotate(T, x->parent);x = T->root;}} else {rbtree_node *w = x->parent->left;if (w->color == RED) {w->color = BLACK;x->parent->color = RED;rbtree_right_rotate(T, x->parent);w = x->parent->left;}if ((w->left->color == BLACK) && (w->right->color == BLACK)) {w->color = RED;x = x->parent;} else {if (w->left->color == BLACK) {w->right->color = BLACK;w->color = RED;rbtree_left_rotate(T, w);w = x->parent->left;}w->color = x->parent->color;x->parent->color = BLACK;w->left->color = BLACK;rbtree_right_rotate(T, x->parent);x = T->root;}}}x->color = BLACK;
}rbtree_node *rbtree_delete(rbtree *T, rbtree_node *z) {rbtree_node *y = T->nil;rbtree_node *x = T->nil;if ((z->left == T->nil) || (z->right == T->nil)) {y = z;} else {y = rbtree_successor(T, z);}if (y->left != T->nil) {x = y->left;} else if (y->right != T->nil) {x = y->right;}x->parent = y->parent;if (y->parent == T->nil) {T->root = x;} else if (y == y->parent->left) {y->parent->left = x;} else {y->parent->right = x;}if (y != z) {z->key = y->key;z->value = y->value;}if (y->color == BLACK) {rbtree_delete_fixup(T, x);}return y;
}rbtree_node *rbtree_search(rbtree *T, KEY_TYPE key) {rbtree_node *node = T->root;while (node != T->nil) {if (key < node->key) {node = node->left;} else if (key > node->key) {node = node->right;} else {return node;}	}return T->nil;
}void rbtree_traversal(rbtree *T, rbtree_node *node) {if (node != T->nil) {rbtree_traversal(T, node->left);printf("key:%d, color:%d\n", node->key, node->color);rbtree_traversal(T, node->right);}
}int main() {int keyArray[20] = {24,25,13,35,23, 26,67,47,38,98, 20,19,17,49,12, 21,9,18,14,15};rbtree *T = (rbtree *)malloc(sizeof(rbtree));if (T == NULL) {printf("malloc failed\n");return -1;}T->nil = (rbtree_node*)malloc(sizeof(rbtree_node));T->nil->color = BLACK;T->root = T->nil;rbtree_node *node = T->nil;int i = 0;for (i = 0;i < 20;i ++) {node = (rbtree_node*)malloc(sizeof(rbtree_node));node->key = keyArray[i];node->value = NULL;rbtree_insert(T, node);}rbtree_traversal(T, T->root);printf("----------------------------------------\n");for (i = 0;i < 20;i ++) {rbtree_node *node = rbtree_search(T, keyArray[i]);rbtree_node *cur = rbtree_delete(T, node);free(cur);rbtree_traversal(T, T->root);printf("----------------------------------------\n");}}

红黑树节点旋转

在这里插入图片描述
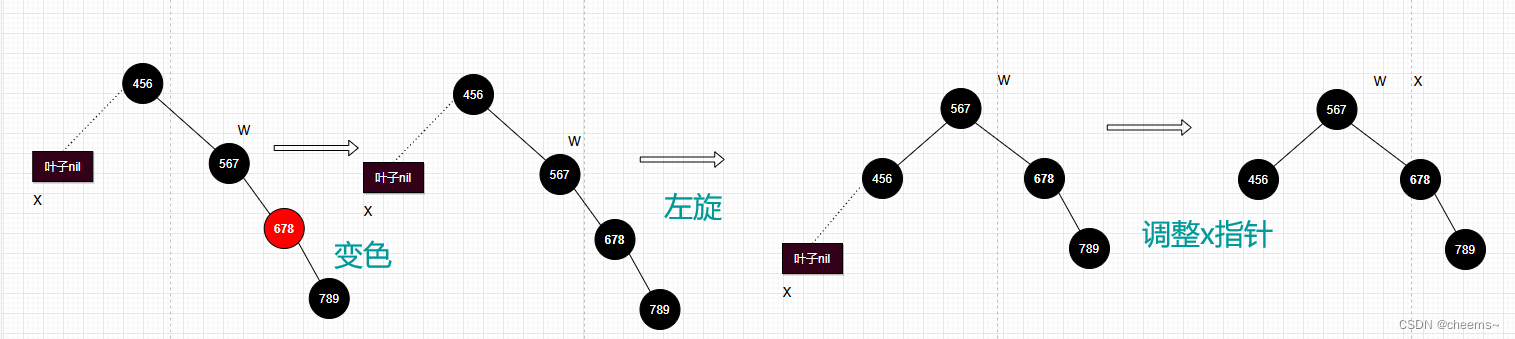
左旋与右旋,一个操作6根指针,成双成对的先x后y,从右下开始直接下层X

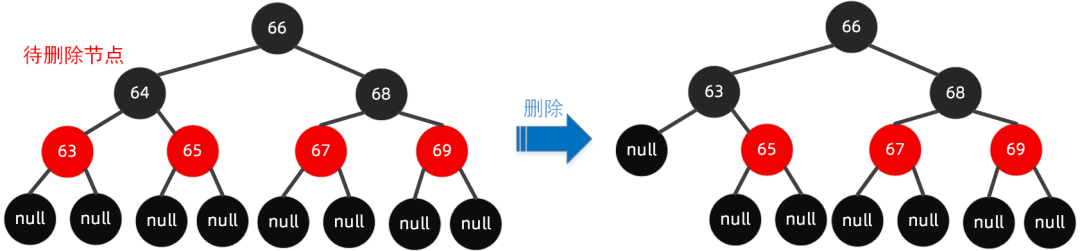
红黑树的添加问题

1.添加之前满足红黑树的性质
它就是一个合法的树,
插入的这个节点是红色的好还是黑色的好?
红色好,是因为红色更容易满足性质,
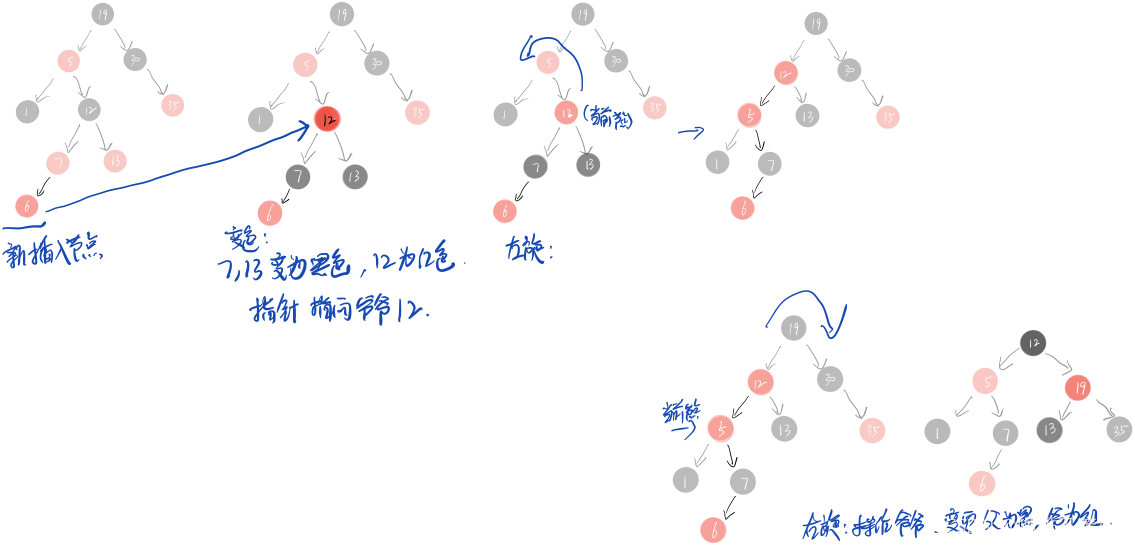
什么时候需要调整?
只有性质四如果一个结点是红的，则它的两个儿子都是黑的违背
违背当前节点是红色的,同时父节点是红色的,从而出现多种情况?
在这里插入图片描述
父结点是祖父结点的左子树的情况

  1. 叔结点是红色的
    在这里插入图片描述
  2. 叔结点是黑色的，而且当前结点是右孩子
    在这里插入图片描述
  3. 叔结点是黑色的，而且当前结点是左孩子
    在这里插入图片描述
void rbtree_insert(rbtree *T, rbtree_node *z) {rbtree_node *y = T->nil;rbtree_node *x = T->root;while (x != T->nil) {y = x;if (z->key < x->key) {x = x->left;} else if (z->key > x->key) {x = x->right;} else { //Existreturn ;}}z->parent = y;if (y == T->nil) {T->root = z;} else if (z->key < y->key) {y->left = z;} else {y->right = z;}z->left = T->nil;z->right = T->nil;z->color = RED;rbtree_insert_fixup(T, z);
}void rbtree_delete_fixup(rbtree *T, rbtree_node *x) {while ((x != T->root) && (x->color == BLACK)) {if (x == x->parent->left) {rbtree_node *w= x->parent->right;if (w->color == RED) {w->color = BLACK;x->parent->color = RED;rbtree_left_rotate(T, x->parent);w = x->parent->right;}if ((w->left->color == BLACK) && (w->right->color == BLACK)) {w->color = RED;x = x->parent;} else {if (w->right->color == BLACK) {w->left->color = BLACK;w->color = RED;rbtree_right_rotate(T, w);w = x->parent->right;}w->color = x->parent->color;x->parent->color = BLACK;w->right->color = BLACK;rbtree_left_rotate(T, x->parent);x = T->root;}} else {rbtree_node *w = x->parent->left;if (w->color == RED) {w->color = BLACK;x->parent->color = RED;rbtree_right_rotate(T, x->parent);w = x->parent->left;}if ((w->left->color == BLACK) && (w->right->color == BLACK)) {w->color = RED;x = x->parent;} else {if (w->left->color == BLACK) {w->right->color = BLACK;w->color = RED;rbtree_left_rotate(T, w);w = x->parent->left;}w->color = x->parent->color;x->parent->color = BLACK;w->left->color = BLACK;rbtree_right_rotate(T, x->parent);x = T->root;}}}x->color = BLACK;
}

if 可以?还是while 肯定得是while直到root的根节点始终扣红色,层层迭代
z=z->parent->parent是关键,z一直是红色


http://chatgpt.dhexx.cn/article/Sie907pW.shtml

相关文章

【数据结构】 AVL树与红黑树

【数据结构】 AVL树与红黑树

目录 一.AVL树&#xff08;平衡二叉树&#xff09; 1.1 AVL树的概念 1.2 AVL树的插入 1.3 AVL树插入的实现 1.4 AVL树的旋转 1.5 AVL树的性能 二.红黑树 2.1 红黑树的概念 2.2 红黑树的性质 2.3 红黑树结构 2.4 红黑树的插入操作 2.5 红黑树插入的代码实现 2.6 …
阅读更多...
Nginx中对红黑树的使用

Nginx中对红黑树的使用

nginx哪些地方用了红黑树 一、Nginx定义的红黑树二、Nginx使用红黑树的地方2.1、ngx_cycle2.2、ngx_open_file_cache 总结 一、Nginx定义的红黑树 Nginx定义的红黑树在/src/core/ngx_rbtree.h和/src/core/ngx_rbtree.c。定义了红黑树节点、红黑树、红黑树插入函数等等。 其中…
阅读更多...
为什么要有红黑树？什么是红黑树？画了20张图，看完这篇你就明白了

为什么要有红黑树？什么是红黑树？画了20张图，看完这篇你就明白了

为什么要有红黑树 想必大家对二叉树搜索树都不陌生&#xff0c;首先看一下二叉搜索树的定义&#xff1a; 二叉搜索树&#xff08;Binary Search Tree&#xff09;&#xff0c;或者是一棵空树&#xff0c;或者是具有下列性质的二叉树&#xff1a; 若它的左子树不空&#xff0c;…
阅读更多...
“红黑树”详解丨红黑树的应用场景

“红黑树”详解丨红黑树的应用场景

今天我们要说的红黑树就是就是一棵非严格均衡的二叉树&#xff0c;均衡二叉树又是在二叉搜索树的基础上增加了自动维持平衡的性质&#xff0c;插入、搜索、删除的效率都比较高。红黑树也是实现 TreeMap 存储结构的基石。 文章相关视频讲解&#xff1a; 红黑树在linux中的3种应…
阅读更多...
AVL树与红黑树（RBTree）的概念与区别

AVL树与红黑树（RBTree）的概念与区别

要想了解AVL树与红黑树的区别&#xff0c;首先我们要先知道&#xff0c;这两棵树是属于自平衡二叉树&#xff0c;那么什么是平衡二叉树呢&#xff1f; 一、平衡二叉树 二叉树的每一个节点的左右子树的深度差不超过1。 二、如何实现自平衡&#xff1f; 通过旋转&#xff0c;…
阅读更多...
HashMap 链表与红黑树转换

HashMap 链表与红黑树转换

链表转换为红黑树 //此处遍历链表for (int binCount 0; ; binCount) {//遍历到链表最后一个节点if ((e p.next) null) {p.next newNode(hash, key, value, null);//如果链表元素个数大于等于TREEIFY_THRESHOLDif (binCount > TREEIFY_THRESHOLD - 1) // -1 for 1st//红黑…
阅读更多...
为什么要有红黑树？什么是红黑树？

为什么要有红黑树？什么是红黑树？

为什么要有红黑树 想必大家对二叉树搜索树都不陌生&#xff0c;首先看一下二叉搜索树的定义&#xff1a;二叉搜索树&#xff08;Binary Search Tree&#xff09;&#xff0c;或者是一棵空树&#xff0c;或者是具有下列性质的二叉树&#xff1a; 若它的左子树不空&#xff0c;则…
阅读更多...
HashMap与红黑树

HashMap与红黑树

一、为什么需要HashMap? 在我们写程序的时候经常会遇到数据检索等操作&#xff0c;对于几百个数据的小程序而言&#xff0c;数据的存储方式或是检索策略没有太大影响&#xff0c;但对于大数据&#xff0c;效率就会差很远。 1、线性检索&#xff1a; 线性检索是最为直白的方法…
阅读更多...
数据结构：什么是红黑树？为什么要用红黑树？

数据结构：什么是红黑树？为什么要用红黑树？

本篇主要谈谈对红黑树的理解&#xff0c;大家都晓得JDK8中的hashmap底层是数组链表红黑树实现的&#xff0c;当面试官问你&#xff1a;为啥要加上红黑树实现呢&#xff1f;&#xff1f; 那我们首先从概念来了解一下&#xff1a; 一、什么是红黑树&#xff1f; 红黑树是一个接…
阅读更多...
随处可见的红黑树详解

随处可见的红黑树详解

随处可见的红黑树详解 前言为什么要有红黑树二叉搜索树平衡二叉搜索树红黑树 红黑树的应用场景红黑树的性质&#xff08;重点&#xff09;红黑树的定义红黑树的左旋与右旋红黑树插入结点与插入维护红黑树的三种情况插入结点插入结点后维护红黑树父结点是爷结点是左子树1. 叔结点…
阅读更多...
HashMap-链表与红黑树转换触发条件

HashMap-链表与红黑树转换触发条件

JDK1.8对HashMap进行了很多优化。 例如当一个槽位slot上的链表个数过多时&#xff0c;则会将链表转换为红黑树&#xff0c;以提高查询检索的效率。 访问节点方式&#xff1a;先找到节点所在的数组index索引位置&#xff0c;然后判断节点是什么结构进行遍历。 节点结构是非树…
阅读更多...
9.HashMap里的红黑树是什么

9.HashMap里的红黑树是什么

1. 简介 红黑树是一种自平衡二叉查找树。它的统计性能要好于平衡二叉树&#xff08;AVL树&#xff09;&#xff0c;因此&#xff0c;红黑树在很多地方都有应用。在C STL中&#xff0c;很多部分(目前包括set, multiset, map,multimap)应用了红黑树的变体(SGI STL中的红黑树有一…
阅读更多...
算法：什么是红黑树

算法：什么是红黑树

红黑树的定义 红黑树的英文是“Red-Black Tree”&#xff0c;简称 R-B Tree。它是一种不严格的平衡二叉查找树。顾名思义&#xff0c;红黑树中的节点&#xff0c;一类被标记为黑色&#xff0c;一类被标记为红色。除此之外&#xff0c;一棵红黑树还需要满足这样几个要求&#x…
阅读更多...
pygraphviz的安装与红黑树可视化

pygraphviz的安装与红黑树可视化

大家好&#xff0c;我是小小明&#xff0c;今天我将带大家安装pygraphviz&#xff0c;并通过它对红黑树这种数据结构进行可视化。 pygraphviz的安装与红黑树的可视化 安装graphviz 下载地址&#xff1a;http://www.graphviz.org/download/ windows平台下可以选择&#xff1…
阅读更多...
到底什么是红黑树？

到底什么是红黑树？

到底什么是红黑树&#xff1f; 首先&#xff0c;可以这么简单粗暴的理解&#xff0c;红黑树≈平衡的二叉排序树。 那么很显然&#xff0c;要想弄懂红黑树&#xff0c;得先明白什么是树、二叉树、二叉排序树、平衡树以及不平衡树。下面我们一个个来了解。 1.第一个问题&#x…
阅读更多...
面试常问：什么是红黑树？

面试常问：什么是红黑树？

什么是红黑树&#xff1f; ———————————— 二叉查找树&#xff08;BST&#xff09;具备什么特性呢&#xff1f; 1.左子树上所有结点的值均小于或等于它的根结点的值。 2.右子树上所有结点的值均大于或等于它的根结点的值。 3.左、右子树也分别为二叉排序树。 下图…
阅读更多...
红黑树简介

红黑树简介

一、什么是红黑树 红黑树&#xff08;Red Black Tree&#xff09; 是一种自平衡二叉查找树&#xff0c;是在计算机科学中用到的一种数据结构&#xff0c;典型的用途是实现关联数组。 红黑树是在1972年由Rudolf Bayer发明的&#xff0c;当时被称为平衡二叉B树&#xff08;symme…
阅读更多...
什么是红黑树？

什么是红黑树？

一、红黑树的产生 1.二叉树 定义&#xff1a;二叉树&#xff08;binary tree&#xff09;是指树中节点的度不大于2的有序树&#xff0c;它是一种最简单且最重要的树。二叉树的递归定义为&#xff1a;二叉树是一棵空树&#xff0c;或者是一棵由一个根节点和两棵互不相交的&…
阅读更多...
说说什么是红黑树？

说说什么是红黑树？

分析&回答 红黑树介绍 R-B Tree&#xff0c;全称是Red-Black Tree&#xff0c;又称为“红黑树”&#xff0c;红黑树就是一种平衡的二叉查找树&#xff0c;说他平衡的意思是他不会变成“瘸子”&#xff0c;左腿特别长或者右腿特别长。除了符合二叉查找树的特性之外&#xf…
阅读更多...
漫画：什么是红黑树？（整合版）

漫画：什么是红黑树？（整合版）

前段时间&#xff0c;小灰发布了红黑树相关的文章&#xff0c;分成上下篇来讲解。 这一次&#xff0c;小灰把两篇文章做了整合&#xff0c;并且修正了红黑树删除部分的图片错误&#xff0c;感谢大家的指正。 ————— 第二天 ————— ———————————— 二叉查找…
阅读更多...
推荐文章

Copyright @ 2022~2023