HashMap 链表与红黑树转换

article/2025/6/9 15:54:39

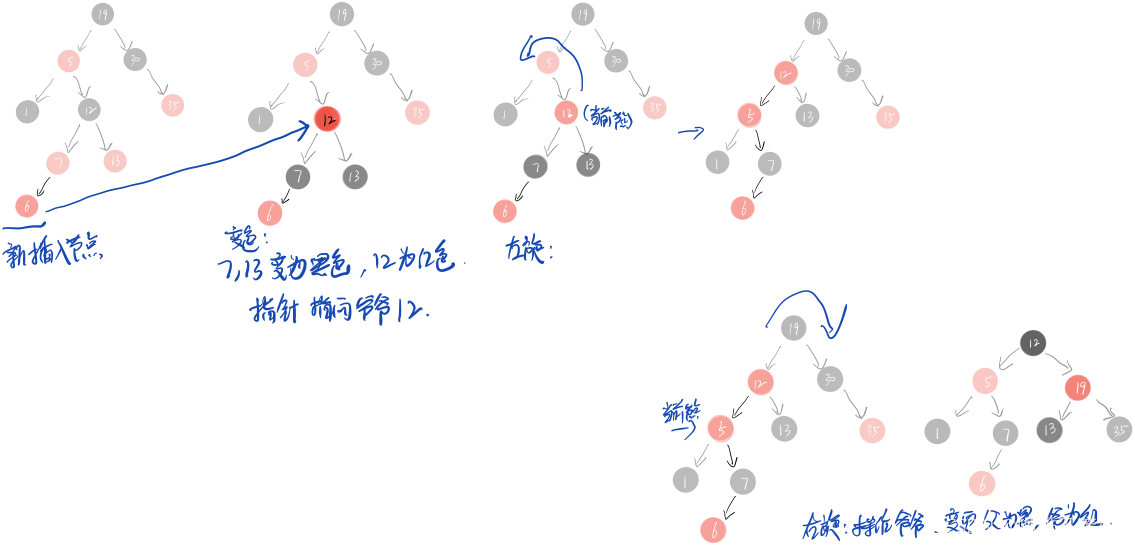
链表转换为红黑树

                //此处遍历链表for (int binCount = 0; ; ++binCount) {//遍历到链表最后一个节点if ((e = p.next) == null) {p.next = newNode(hash, key, value, null);//如果链表元素个数大于等于TREEIFY_THRESHOLDif (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st//红黑树转换逻辑treeifyBin(tab, hash);break;}if (e.hash == hash &&((k = e.key) == key || (key != null && key.equals(k))))break;p = e;}

    static final int MIN_TREEIFY_CAPACITY = 64;static final int UNTREEIFY_THRESHOLD = 6;/*** Replaces all linked nodes in bin at index for given hash unless* table is too small, in which case resizes instead.*/final void treeifyBin(Node<K,V>[] tab, int hash) {int n, index; Node<K,V> e;if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)resize();else if ((e = tab[index = (n - 1) & hash]) != null) {TreeNode<K,V> hd = null, tl = null;do {TreeNode<K,V> p = replacementTreeNode(e, null);if (tl == null)hd = p;else {p.prev = tl;tl.next = p;}tl = p;} while ((e = e.next) != null);if ((tab[index] = hd) != null)hd.treeify(tab);}}

可以看到在treeifyBin中并不是简单地将链表转换为红黑树，而是先判断table的长度是否大于64，如果小于64，就通过扩容的方式来解决，避免红黑树结构化.
个人觉得链表长度大于8有两种情况：

table长度足够，hash冲突过多
table长度太小,但是在计算table下标的时候,导致很多hash不一致的key计算的下标一致

所以扩容后链表长度变短，读写效率自然提高。另外，扩容相对于转换为红黑树的好处在于可以保证数据结构更简单。并不是链表长度超过8就一定会转换成红黑树，而是先尝试扩容。

红黑树转换为链表

基本思想是当红黑树中的元素减少并小于一定数量时，会切换回链表。

而元素减少有两种情况：

调用map的remove方法删除元素
resize的时候，对红黑树进行了拆分

1、hashMap的remove方法，会进入到removeNode方法，找到要删除的节点，并判断node类型是否为treeNode，然后进入删除红黑树节点逻辑的removeTreeNode方法中，该方法有关解除红黑树结构的分支如下

 //判断是否要解除红黑树的条件
if (root == null || root.right == null ||(rl = root.left) == null || rl.left == null) {tab[index] = first.untreeify(map);  // too smallreturn;}

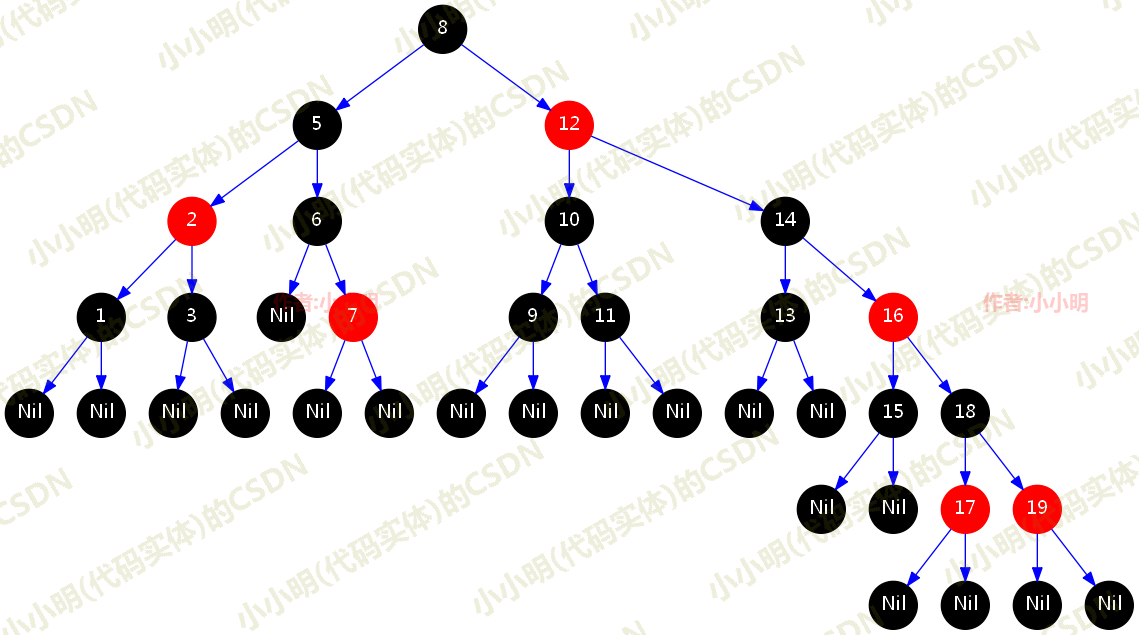
此时是通过红黑树根节点及其子节点是否为空来判断，而满足该条件的最大红黑树结构如下：
在这里插入图片描述
节点数为10，大于 UNTREEIFY_THRESHOLD（6），但是根据该方法的逻辑判断，是需要转换为链表的

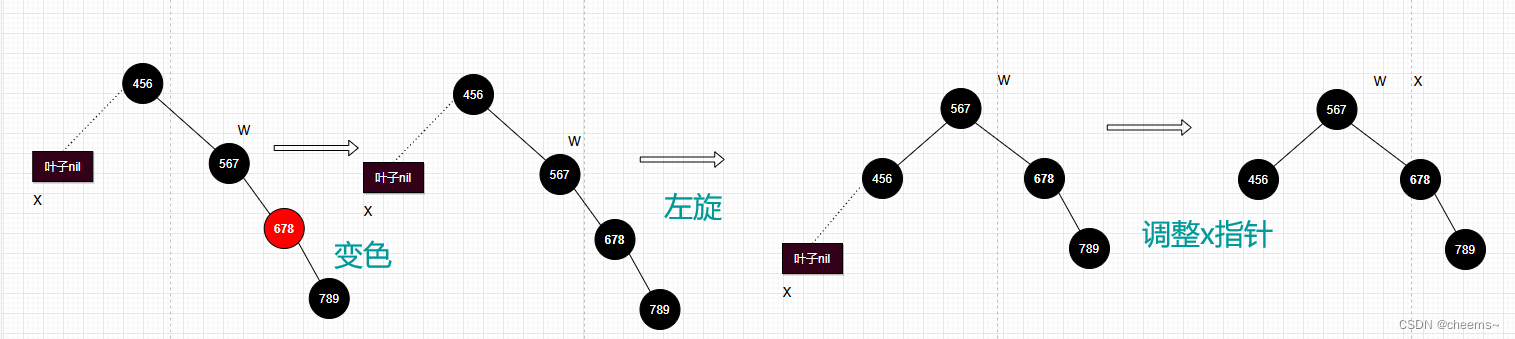
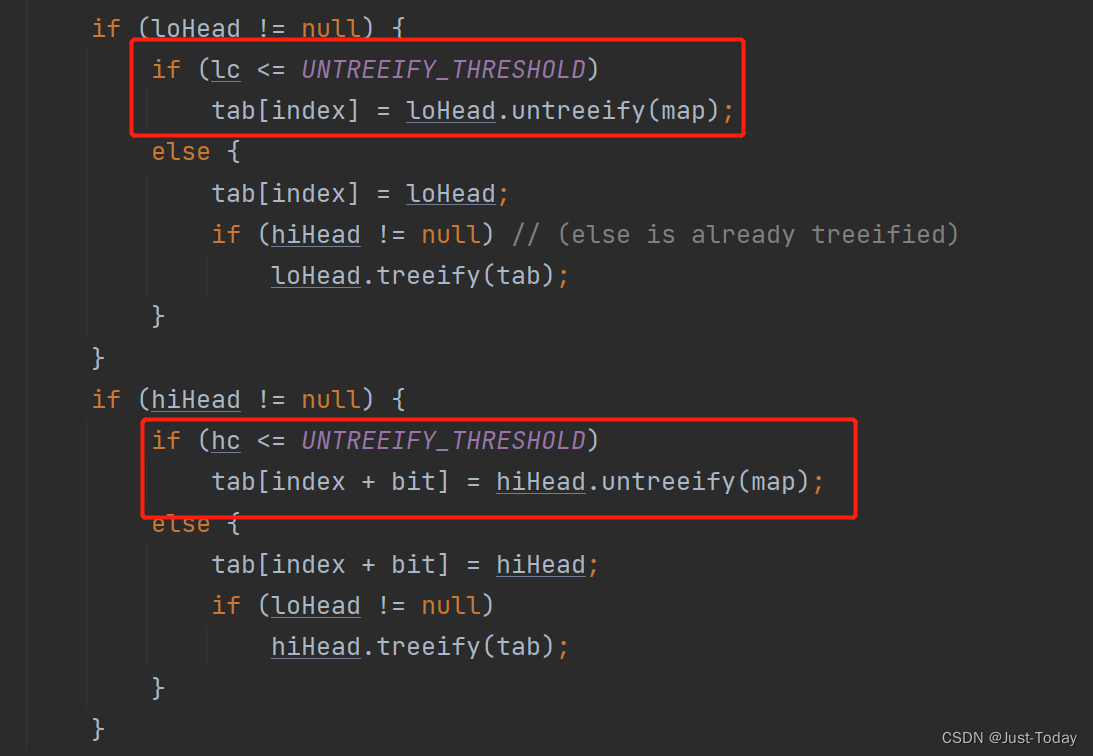
2、resize的时候，判断节点类型，如果是链表，则将链表拆分，如果是TreeNode，则执行TreeNode的split方法分割红黑树，而split方法中将红黑树转换为链表的分支如下

//在这之前的逻辑是将红黑树每个节点的hash和一个bit进行&运算，
//根据运算结果将树划分为两棵红黑树，lc表示其中一棵树的节点数
if (lc <= UNTREEIFY_THRESHOLD)tab[index] = loHead.untreeify(map);else {tab[index] = loHead;if (hiHead != null) // (else is already treeified)loHead.treeify(tab);}