今天我们要说的红黑树就是就是一棵非严格均衡的二叉树，均衡二叉树又是在二叉搜索树的基础上增加了自动维持平衡的性质，插入、搜索、删除的效率都比较高。红黑树也是实现 TreeMap 存储结构的基石。

文章相关视频讲解：

红黑树在linux中的3种应用场景，听完受益匪浅

5种红黑树的场景，从Linux内核谈到Nginx源码，听完醍醐灌顶

c/c++Linux后台服务器开发高级架构师视频资料

二叉搜索树

二叉搜索树又叫二叉查找树、二叉排序树，我们先看一下典型的二叉搜索树，这样的二叉树有何规则特点呢？

二叉搜索树有如下几个特点：

• 节点的左子树小于节点本身
• 节点的右子树大于节点本身
• 左右子树同样为二叉搜索树

下图就是一棵典型的二叉搜索树：

 

 二叉搜索树是均衡二叉树的基础，我们看一下它的搜索步骤如何。我们要从二叉树中找到值为 58 的节点。

第一步：首先查找到根节点，值为 60 的节点。

 

第二步：比较我们要找的值 58 与该节点的大小。

如果等于，那么恭喜，已经找到；如果小于，继续找左子树；如果大于，那么找右子树。

很明显 58<60，因此我们找到左子树的节点 56，此时我们已经定位到了节点 56。

 

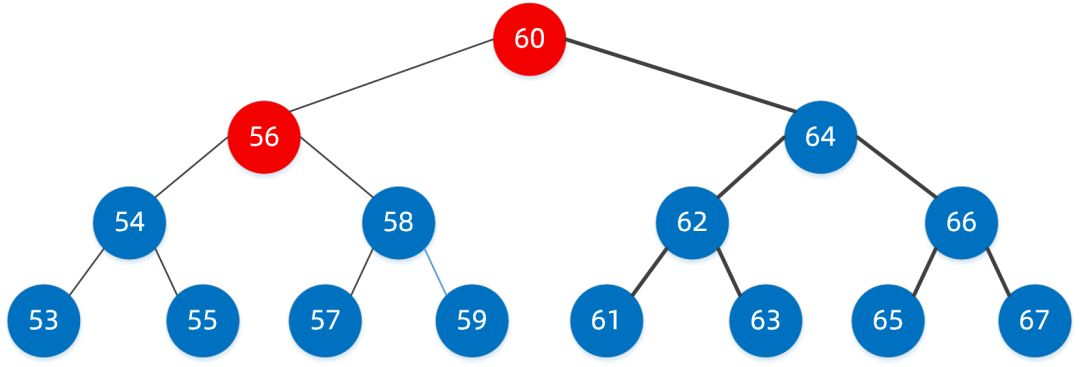
 第三步：按照第二步的规则继续找。

58>56 我们需要继续找右子树，定位到了右子树节点 58，恭喜，此时我们已经找到了。

 

我们经过三步就已经找到了，其实就是我们平时所说的二分查找，这种二叉搜索树好像查找效率很高，但同样它也有缺陷，如下面这样的二叉搜索树。

 

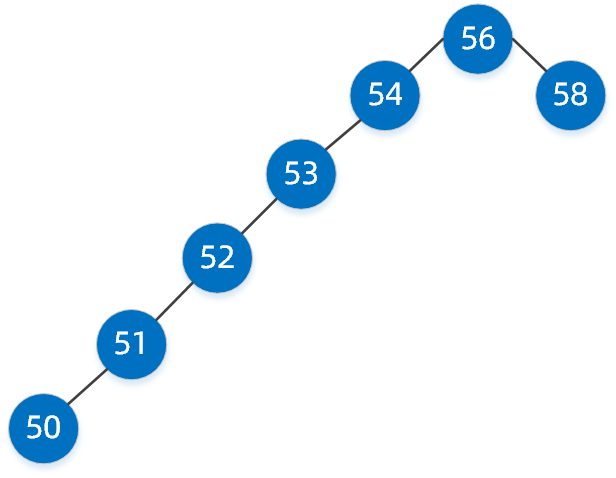
看到这样的二叉搜索树是否很别扭，典型的大长腿瘸子，但它也是二叉搜索树，如果我们要找值为 50 的节点，基本上和单链表查询没多大区别了，性能将大打折扣。

这个时候我们的均衡二叉树就粉墨登场了，均衡二叉树就是在二叉搜索树的基础上添加了自动维持平衡的性质。

上面的大长腿瘸子二叉搜索树经过自动平衡后，可能就成为了下面这样的二叉树。

 

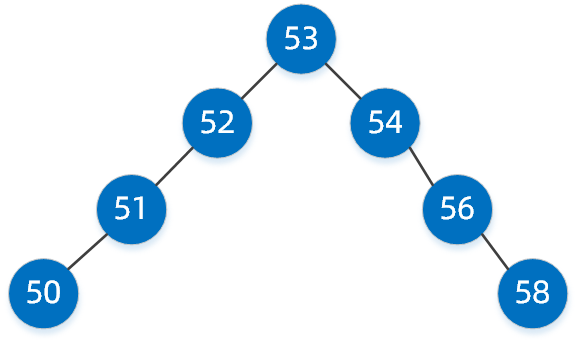
经过了自动平衡，再去找值为 50 的节点，查找性能将提升很多。红黑树就是非严格均衡的二叉搜索树。

红黑树规则特点

红黑树具体有哪些规则特点呢？具体如下：

• 节点分为红色或者黑色。
• 根节点必为黑色。
• 叶子节点都为黑色，且为 null。
• 连接红色节点的两个子节点都为黑色（红黑树不会出现相邻的红色节点）。
• 从任意节点出发，到其每个叶子节点的路径中包含相同数量的黑色节点。
• 新加入到红黑树的节点为红色节点。

规则看着好像挺多，没错，因为红黑树也是均衡二叉树，需要具备自动维持平衡的性质，上面的 6 条就是红黑树给出的自动维持平衡所需要具备的规则。

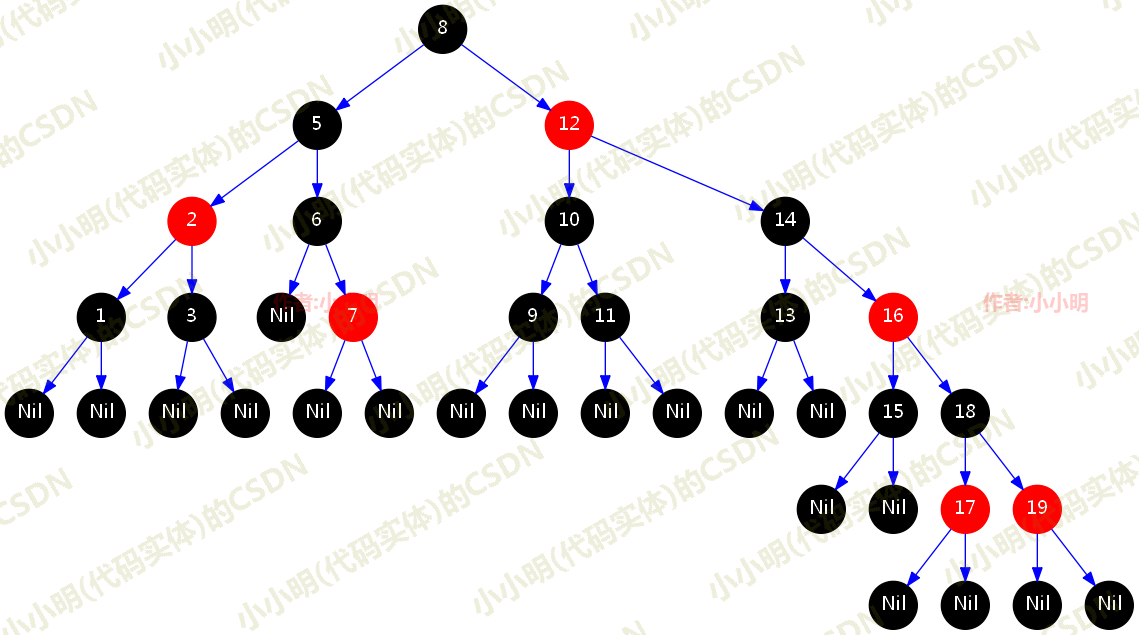
我们看一看一个典型的红黑树到底是什么样儿？

 

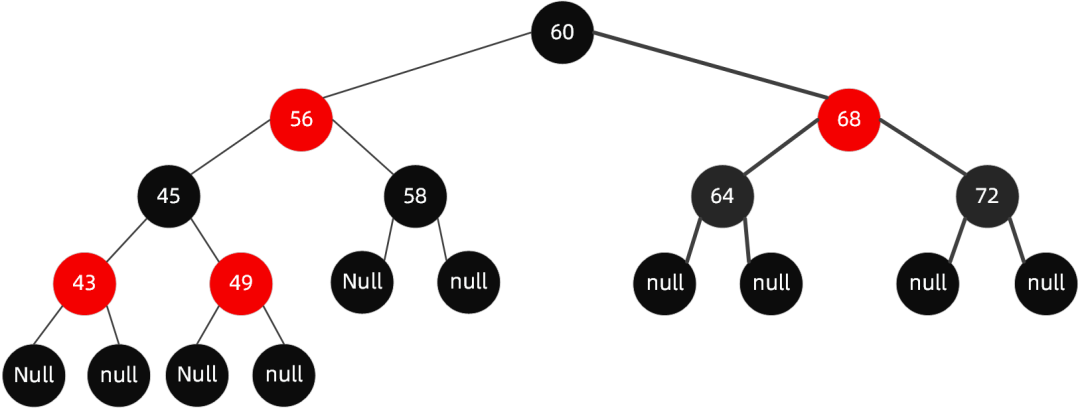
 首先解读一下规则，除了字面上看到的意思，还隐藏了哪些意思呢？

①从根节点到叶子节点的最长路径不大于最短路径的 2 倍

怎么样的路径算最短路径？从规则 5 中，我们知道从根节点到每个叶子节点的黑色节点数量是一样的，那么纯由黑色节点组成的路径就是最短路径。

什么样的路径算是最长路径？根据规则 4 和规则 3，若有红色节点，则必然有一个连接的黑色节点，当红色节点和黑色节点数量相同时，就是最长路径，也就是黑色节点（或红色节点）*2。

②为什么说新加入到红黑树中的节点为红色节点

从规则 4 中知道，当前红黑树中从根节点到每个叶子节点的黑色节点数量是一样的，此时假如新的是黑色节点的话，必然破坏规则。

但加入红色节点却不一定，除非其父节点就是红色节点，因此加入红色节点，破坏规则的可能性小一些，下面我们也会举例来说明。

什么情况下，红黑树的结构会被破坏呢？破坏后又怎么维持平衡，维持平衡主要通过两种方式【变色】和【旋转】，【旋转】又分【左旋】和【右旋】，两种方式可相互结合。

下面我们从插入和删除两种场景来举例说明。

红黑树节点插入：

当我们插入值为 66 的节点时，红黑树变成了这样：

 

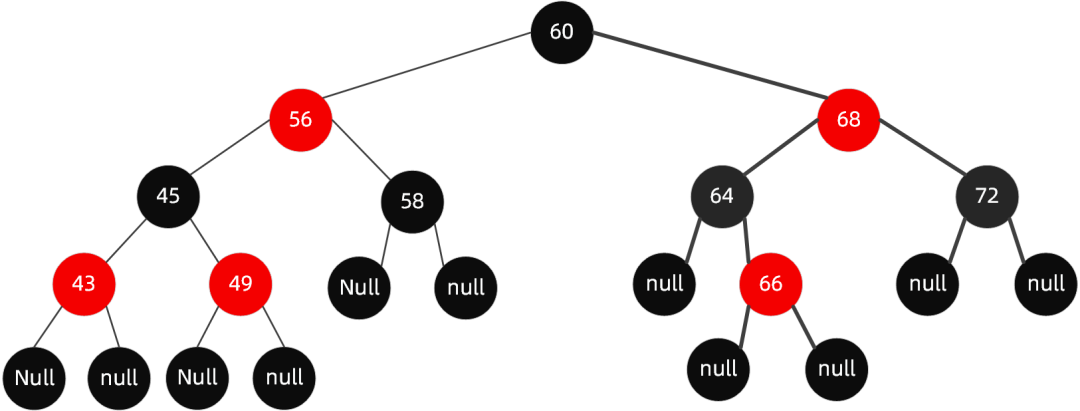
很明显，这个时候结构依然遵循着上述 6 大规则，无需启动自动平衡机制调整节点平衡状态。

如果再向里面插入值为 51 的节点，这个时候红黑树变成了这样：

 

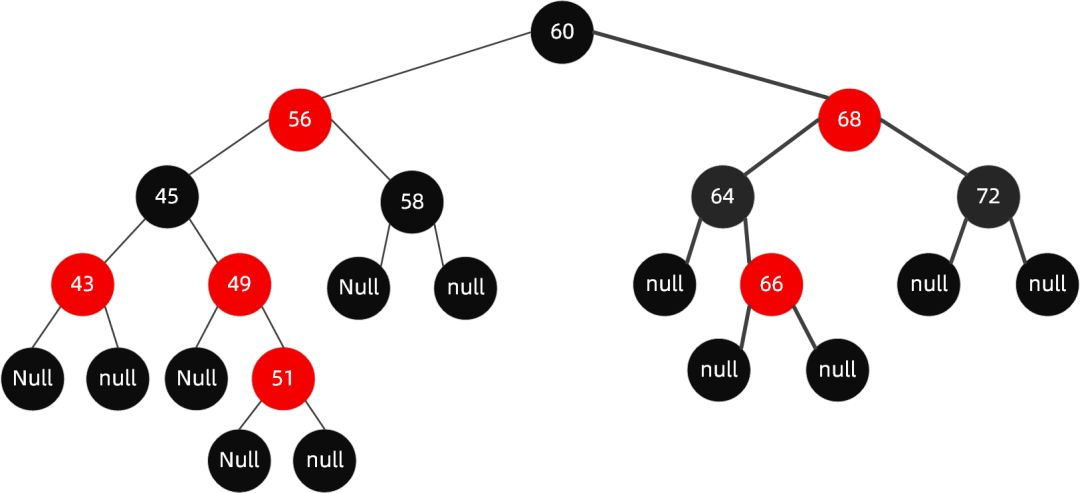
很明显现在的结构不遵循规则 4 了，这个时候就需要启动自动平衡机制调整节点平衡状态。

关于C/C++ Linux后端开发网络底层原理知识学习提升 点击 学习资料 获取，内容知识点包括Linux，Nginx，ZeroMQ，MySQL，Redis，线程池，MongoDB，ZK，Linux内核，CDN，P2P，epoll，Docker，TCP/IP，协程，DPDK等等。

变色：

我们可以通过变色的方式，使结构满足红黑树的规则：

• 首先解决结构不遵循规则 4 这一点（红色节点相连，节点 49-51），需将节点 49 改为黑色。
• 此时我们发现又违反了规则 5（56-49-51-XX 路径中黑色节点超过了其他路径），那么我们将节点 45 改为红色节点。
• 哈哈，妹的，又违反了规则 4（红色节点相连，节点 56-45-43），那么我们将节点 56 和节点 43 改为黑色节点。
• 但是我们发现此时又违反了规则 5（60-56-XX 路径的黑色节点比 60-68-XX 的黑色节点多），因此我们需要调整节点 68 为黑色。
• 完成！

 

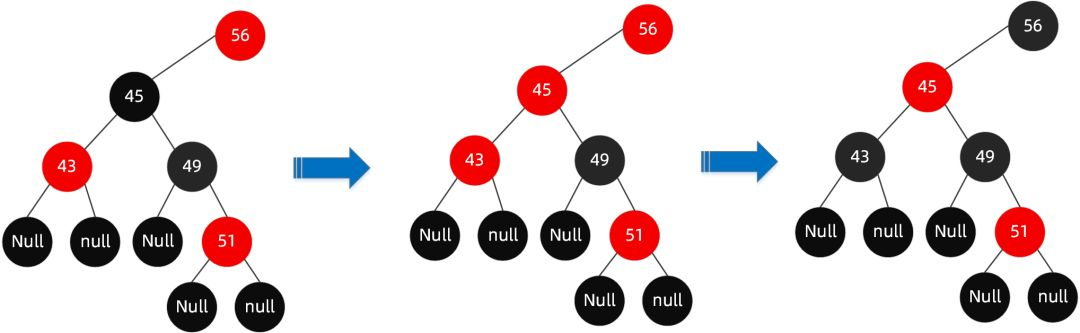
最终调整完成后的树为：

 

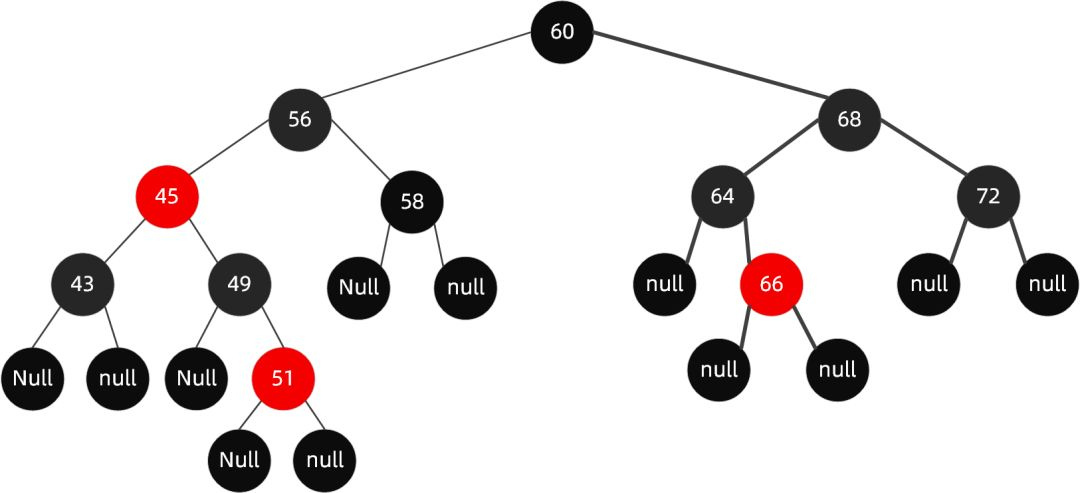
但并不是什么时候都那么幸运，可以直接通过变色就达成目的，大多数时候还需要通过旋转来解决。

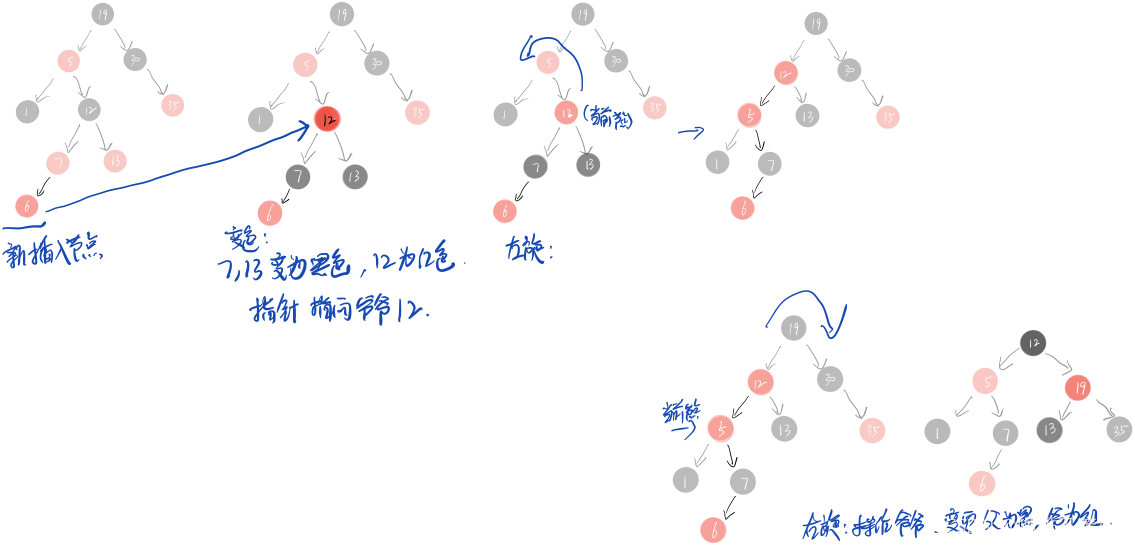
如在下面这棵树的基础上，加入节点 65：

 

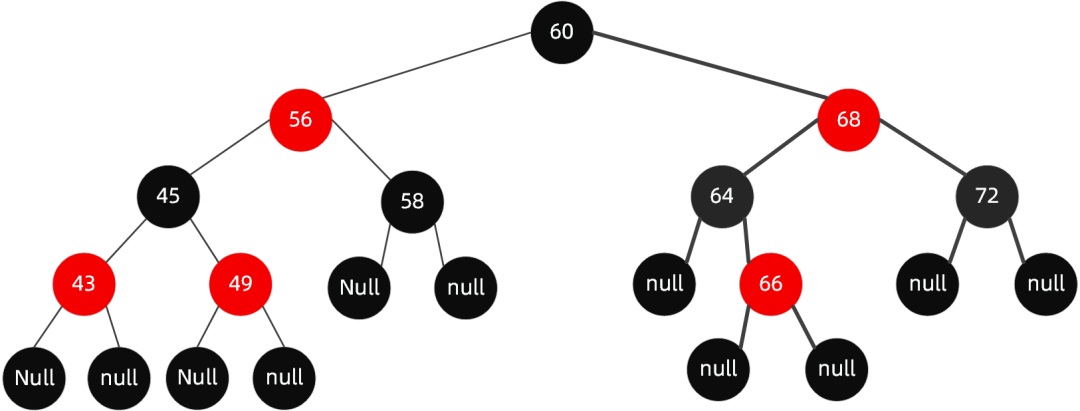
插入节点 65 后进行以下步骤：

 

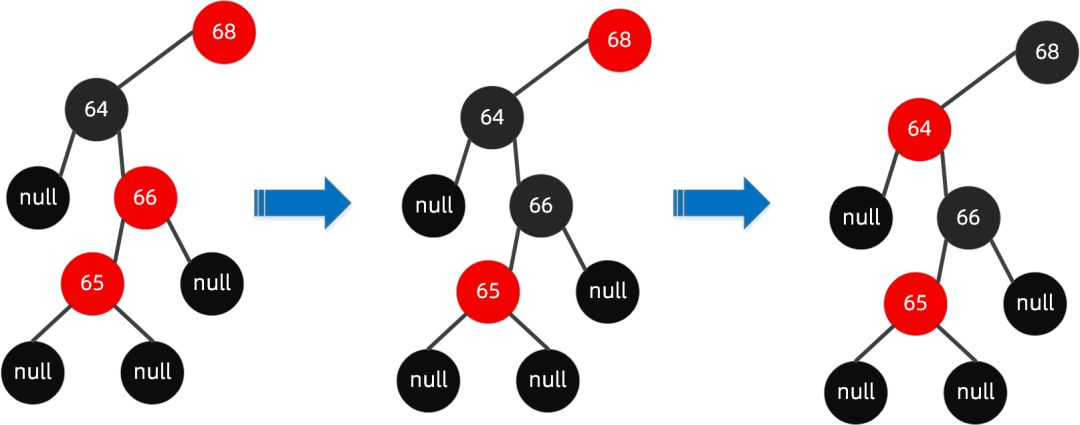
这个时候，你会发现对于节点 64 无论是红色节点还是黑色节点，都会违反规则 5，路径中的黑色节点始终无法达成一致，这个时候仅通过【变色】已经无法达成目的。

我们需要通过旋转操作，当然【旋转】操作一般还需要搭配【变色】操作。旋转包括【左旋】和【右旋】。

左旋：逆时针旋转两个节点，让一个节点被其右子节点取代，而该节点成为右子节点的左子节点。

左旋操作步骤如下：首先断开节点 PL 与右子节点 G 的关系，同时将其右子节点的引用指向节点 C2；然后断开节点 G 与左子节点 C2 的关系，同时将 G 的左子节点的应用指向节点 PL。

 

右旋：顺时针旋转两个节点，让一个节点被其左子节点取代，而该节点成为左子节点的右子节点。

右旋操作步骤如下：首先断开节点 G 与左子节点 PL 的关系，同时将其左子节点的引用指向节点 C2；然后断开节点 PL 与右子节点 C2 的关系，同时将 PL 的右子节点的应用指向节点 G。

 

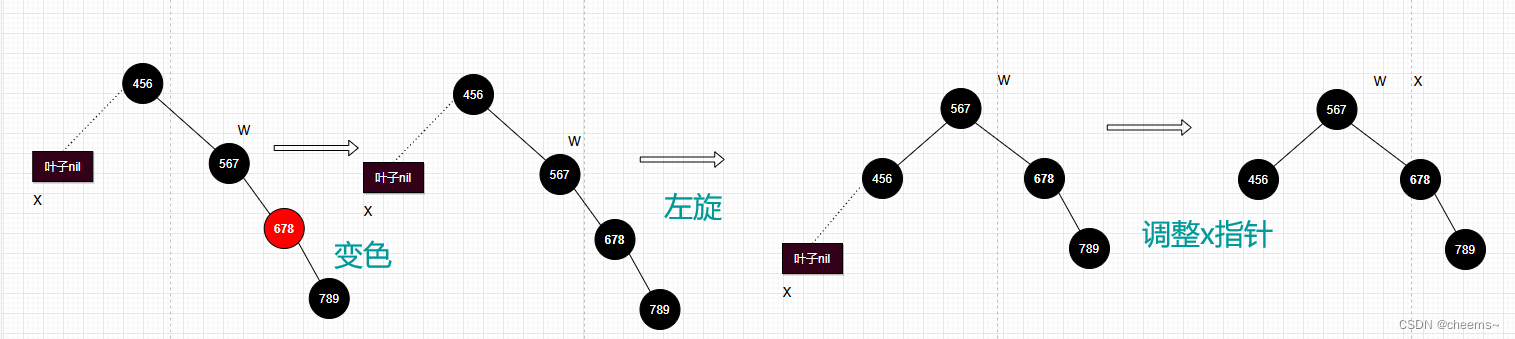
无法通过变色而进行旋转的场景分为以下四种：

第一种：左左节点旋转

这种情况下，父节点和插入的节点都是左节点，如下图(旋转原始图1)这种情况下，我们要插入节点 65。

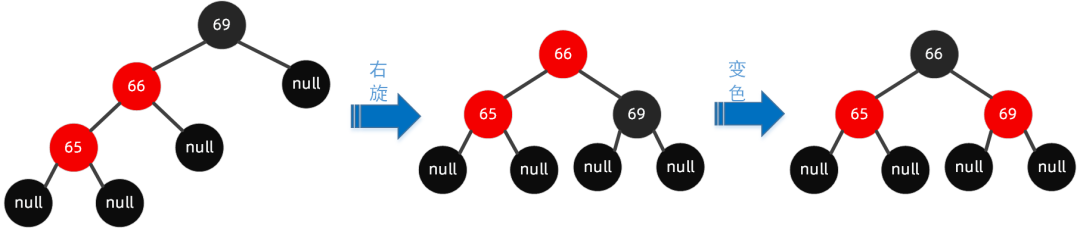
规则如下：以祖父节点【右旋】，搭配【变色】。

 

按照规则，步骤如下：

 

第二种：左右节点旋转

这种情况下，父节点是左节点，插入的节点是右节点，在旋转原始图 1 中，我们要插入节点 67。

规则如下：先父节点【左旋】，然后祖父节点【右旋】，搭配【变色】。

按照规则，步骤如下：

 

第三种：右左节点旋转

这种情况下，父节点是右节点，插入的节点是左节点，如下图（旋转原始图 2）这种情况，我们要插入节点 68。

规则如下：先父节点【右旋】，然后祖父节点【左旋】，搭配【变色】。

 

按照规则，步骤如下：

 

第四种：右右节点旋转

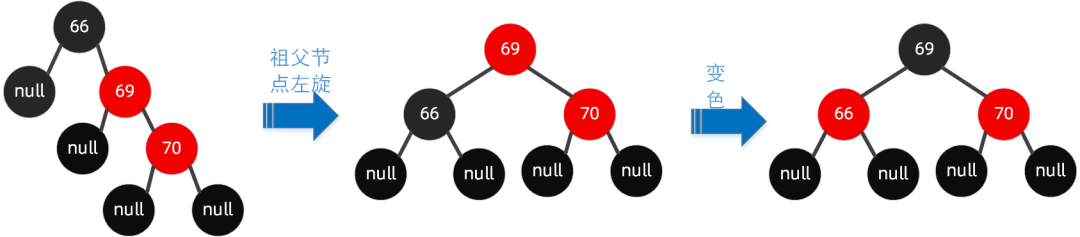
这种情况下，父节点和插入的节点都是右节点，在旋转原始图 2 中，我们要插入节点 70。

规则如下：以祖父节点【左旋】，搭配【变色】。

按照规则，步骤如下：

 

红黑树插入总结

红黑树插入总结如下图：

 

红黑树节点删除:

相比较于红黑树的节点插入，删除节点更为复杂，我们从子节点是否为 null 和红色为思考维度来讨论。

子节点至少有一个为 null

当待删除的节点的子节点至少有一个为 null 节点时，删除了该节点后，将其有值的节点取代当前节点即可。

若都为 null，则将当前节点设置为 null，当然如果违反规则了，则按需调整，如【变色】以及【旋转】。

 

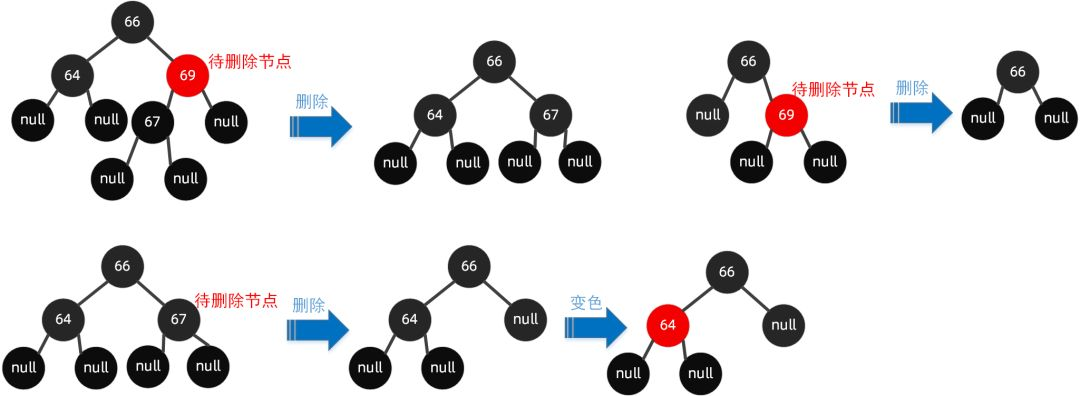
子节点都是非 null 节点

这种情况下：

第一步：找到该节点的前驱或者后继。

前驱：左子树中值最大的节点（可得出其最多只有一个非 null 子节点，可能都为 null）。

后继：右子树中值最小的节点（可得出其最多只有一个非 null 子节点，可能都为 null）。

前驱和后继都是值最接近该节点值的节点，类似于该节点.prev=前驱，该节点.next=后继。

第二步：将前驱或者后继的值复制到该节点中，然后删掉前驱或者后继。

如果删除的是左节点，则将前驱的值复制到该节点中，然后删除前驱；如果删除的是右节点，则将后继的值复制到该节点中，然后删除后继。

这相当于是一种“取巧”的方法，我们删除节点的目的是使该节点的值在红黑树上不存在。

因此专注于该目的，我们并不关注删除节点时是否真是我们想删除的那个节点，同时我们也不需考虑树结构的变化，因为树的结构本身就会因为自动平衡机制而经常进行调整。

前面我们已经说了，我们要删除的实际上是前驱或者后继，因此我们就以前驱为主线来讲解。

后继的学习可参考前驱，包括下面几种情况：

①前驱为黑色节点，并且有一个非 null 子节点

 

分析：因为要删除的是左节点 64，找到该节点的前驱 63；然后用前驱的值 63替换待删除节点的值 64，此时两个节点（待删除节点和前驱）的值都为 63；

删除前驱 63，此时成为上图过程中间环节，但我们发现其不符合红黑树规则 4，因此需要进行自动平衡调整。这里直接通过【变色】即可完成。

②前驱为黑色节点，同时子节点都为 null

 

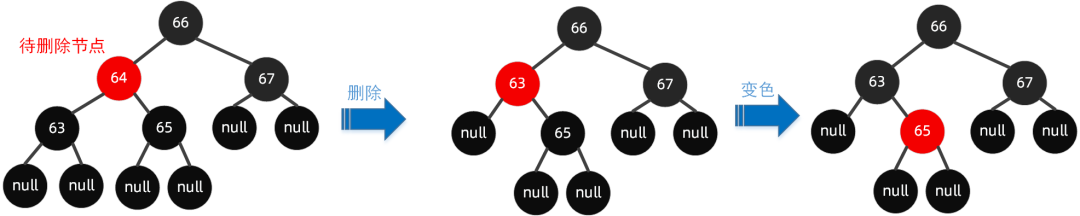
分析：因为要删除的是左节点 64，找到该节点的前驱 63；然后用前驱的值 63 替换待删除节点的值 64，此时两个节点（待删除节点和前驱）的值都为 63。

删除前驱 63，此时成为上图过程中间环节，但我们发现其不符合红黑树规则 5，因此需要进行自动平衡调整。这里直接通过【变色】即可完成。

③前驱为红色节点，同时子节点都为 null

 

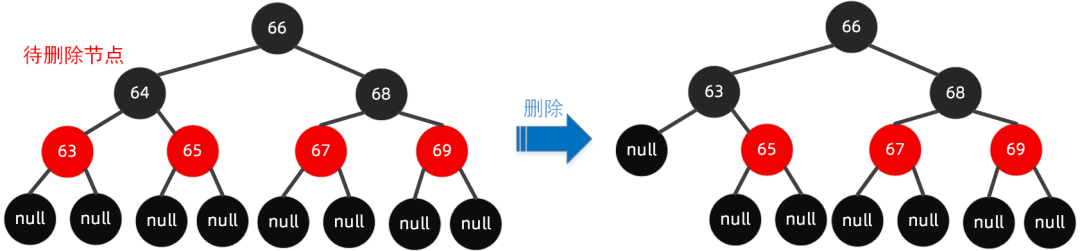
分析：因为要删除的是左节点 64，找到该节点的前驱 63；然后用前驱的值 63替换待删除节点的值 64，此时两个节点（待删除节点和前驱）的值都为 63；删除前驱 63，树的结构并没有打破规则。

红黑树删除总结

红黑树删除的情况比较多，但也就存在以下情况：

• 删除的是根节点，则直接将根节点置为 null。
• 待删除节点的左右子节点都为 null，删除时将该节点置为 null。
• 待删除节点的左右子节点有一个有值，则用有值的节点替换该节点即可。
• 待删除节点的左右子节点都不为 null，则找前驱或者后继，将前驱或者后继的值复制到该节点中，然后删除前驱或者后继。
• 节点删除后可能会造成红黑树的不平衡，这时我们需通过【变色】+【旋转】的方式来调整，使之平衡，上面也给出了例子，建议大家多多练习，而不必背下来。

总结

本文主要介绍了红黑树的相关原理，首先红黑树的基础二叉搜索树，我们先简单说了一下二叉搜索树，并且讲了一下搜索的流程。

然后就针对红黑树的六大规则特点，红黑树的插入操作，删除操作，都使用了大量的图形来加以说明。

红黑树的使用非常广泛，如 TreeMap 和 TreeSet 都是基于红黑树实现的，而 JDK8 中 HashMap 当链表长度大于 8 时也会转化为红黑树。