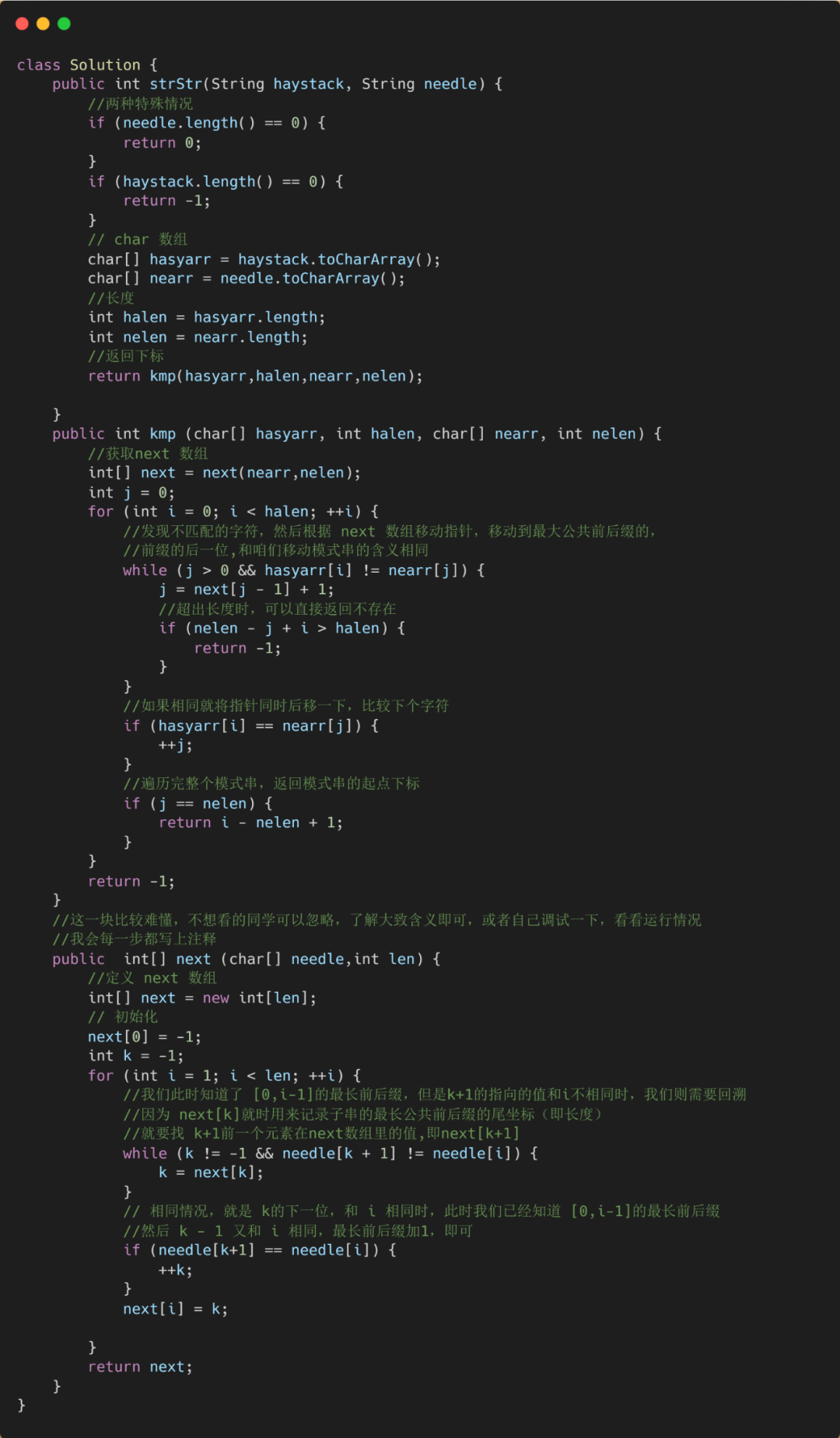
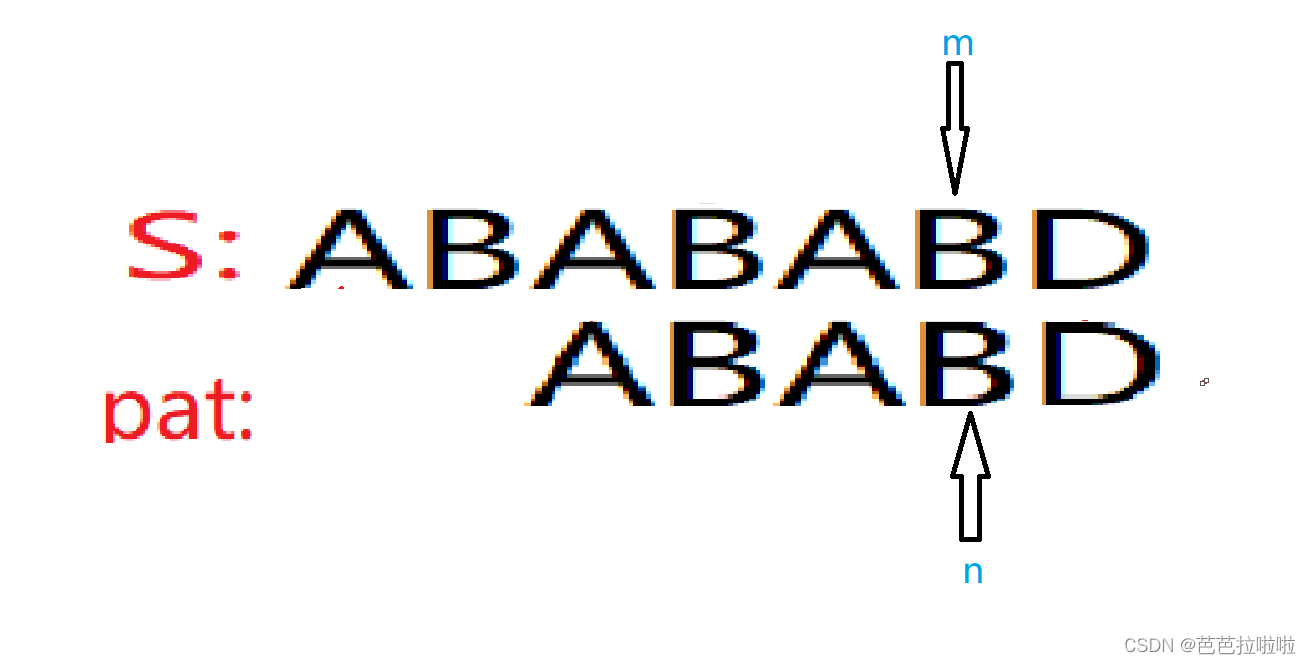字符串匹配算法之KMP算法(图例详解)
- 1.字符串匹配算法及暴力算法
- 1.1 简介
- 1.2 示例题目
- 2.KMP算法(Knuth-Morris-Pratt algorith)
- 2.1 朴素算法的缺点
- 2.2 KMP算法
- 2.2.1 KMP算法中的前缀算法
- 2.2.1.1 前缀函数pi的定义
- 2.2.1.2 前缀函数pi的例子
- 2.2.1.3 前缀函数的代码
- 2.2.2 KMP算法
- 2.2.2.1 KMP算法实例
- 2.2.2.2 KMP算法的代码
1.字符串匹配算法及暴力算法
在字符串匹配算法之暴力做法(朴素算法)我这篇文章已经详细介绍了字符串匹配算法以及它的暴力算法。现在简单复习一下。
1.1 简介
字符串匹配算法又称模式匹配(pattern matching)。该问题可以概括为「给定字符串S和T,在主串S中寻找子串T」。字符T称为模式串 (pattern)。
1.2 示例题目
还是使用来自leetcode 28. 实现 strStr()的这道题。
实现 strStr() 函数。
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串出现的第一个位置(下标从 0 开始)。如果不存在,则返回 -1 。
示例 1:输入: haystack = "hello", needle = "ll" 输出: 2
2.KMP算法(Knuth-Morris-Pratt algorith)
2.1 朴素算法的缺点
在介绍KMP算法之前,我们先回顾一下朴素算法的缺点,有助于我们更好地理解KMP算法。
先看一下这个例子:
txt[] = “AAAAAAAAAAAAAAAAAB”
pat[] = “AAAAB”
如果是朴素算法一个一个对比的话,pat[]一个一个地右移。
第一步:
第二步:
第三步:
\
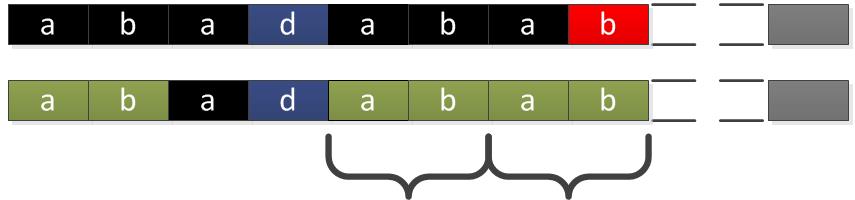
而其实我们在第一步时就已经匹配过中间的3个A了。

这就是朴素算法重复的部分,而KMP算法就将重复的部分跳过了。
2.2 KMP算法
KMP算法是如何跳过这一部分的,我们首先需要了解前缀函数。
2.2.1 KMP算法中的前缀算法
2.2.1.1 前缀函数pi的定义
给定一个长度为n的字符串s,其 前缀函数 被定义为一个长度为n的数组p[]。 其中p[i] 的定义是:
- 如果子串
s[0...i]有一对相等的真前缀与真后缀:s[0...k-1]和s[i-(k-1)...i],那么p[i]就是这个相等的真前缀(或者真后缀,因为它们相等子串的长度,也就是p[i] = k; - 如果不止有一对相等的,那么
p[i]就是其中最长的那一对的长度; - 如果没有相等的,那么
s[i]=0。
简单来说p[i]就是子串s[0...i]最长的相等的真前缀与真后缀的长度。
用数学语言描述如下:
p [ i ] = m a x k = 0... i { k : s [ 0... k − 1 ] = s [ i − ( k − 1 ) ] . . . i } p[i] = max_{k=0...i}\{k:s[0...k-1] = s[i-(k-1)]...i\} p[i]=maxk=0...i{k:s[0...k−1]=s[i−(k−1)]...i}
特别地,规定p[0]=0。
2.2.1.2 前缀函数pi的例子
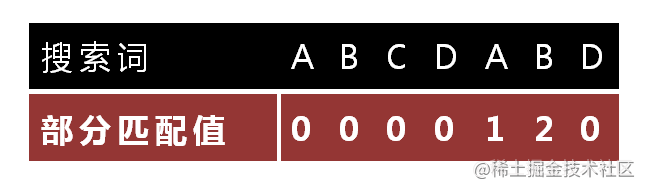
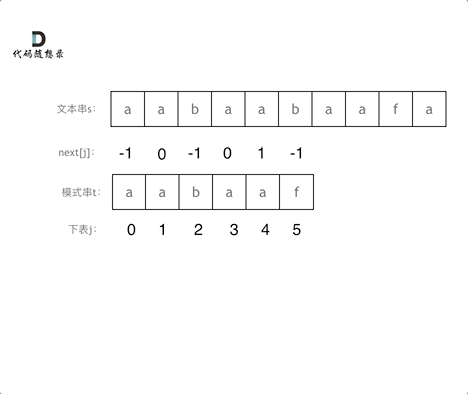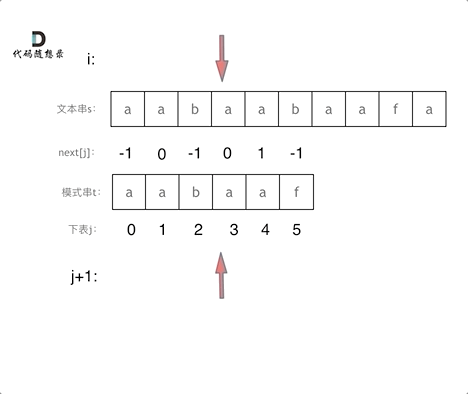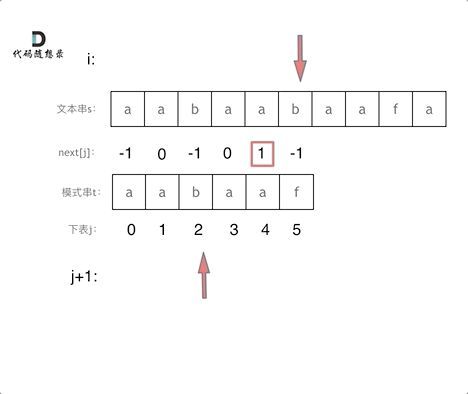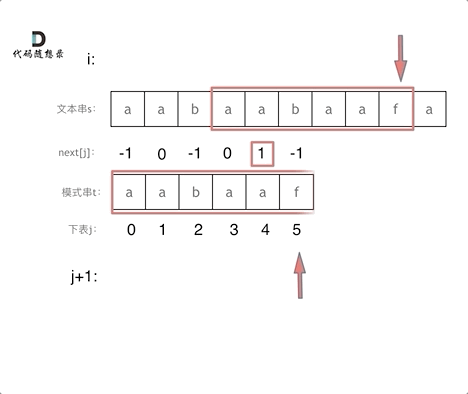
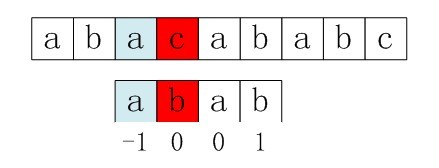
前缀函数求的也就是图中的“部分匹配值”,而"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。
以图中的"ABCDABD"为例,
1.首先需要找出ABCDABD这一串字符串的所有前缀
- A
- AB
- ABC
- ABCD
- ABCDA
- ABCDAB
- ABCDABD
2.然后找出每个前缀字符的最长公共前后缀 - "A"的前缀和后缀都为空集,共有元素的长度为
0; - "AB"的前缀为[A],后缀为[B],共有元素的长度为
0; - "ABC"的前缀为[A, AB],后缀为[BC, C],共有元素的长度
0; - "ABCD"的前缀为[A, AB, ABC],后缀为[BCD, CD, D],共有元素的长度为
0; - “ABCDA"的前缀为[A, AB, ABC, ABCD],后缀为[BCDA, CDA, DA, A],共有元素为"A”,长度为
1; - “ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA],后缀为[BCDAB, CDAB, DAB, AB, B],共有元素为"AB”,长度为
2; - "ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB],后缀为[BCDABD, CDABD, DABD, ABD, BD, D],共有元素的长度为
0。
3.然后就形成了部分匹配值(prefix table)
每个前缀字符的最长公共前后缀放在一起就形成了部分匹配表,也就是: - 0 0 0 0 1 2 0
和图里也是一样的。
2.2.1.3 前缀函数的代码
以下是伪代码:
COMPUTE-PREFIX-FUNCTION(P)
m ← length[P]
π[1] ← 0
k ← 0
for q ← 2 to mdo while k > 0 and P[k + 1] ≠ P[q]do k ← π[k]if P[k + 1] = P[q]then k ← k + 1π[q] ← k
return π
然后是C++版本的实现:
// C++ Version
vector<int> prefix_function(string s) {int n = (int)s.length();vector<int> pi(n);for (int i = 1; i < n; i++)for (int j = i; j >= 0; j--)if (s.substr(0, j) == s.substr(i - j + 1, j)) {pi[i] = j;break;}return pi;
}
2.2.2 KMP算法
现在终于可以讲KMP算法了,讲完前缀函数,KMP算法其实以及算完成了70%。
2.2.2.1 KMP算法实例
我们用之前用过的这个例子:
txt[] = “BBC ABCDAB ABCDABCDABDE”
pat[] = “ABCDABD”
按照上面的步骤我们已经学会如何写出部分匹配表
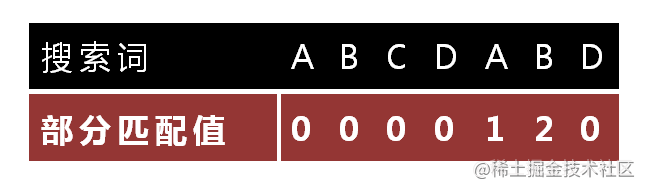
然后我们开始匹配,前面先跳过一直到有重复的字符串中:
1.首先开始对比,一直到D:

已知空格与D不匹配时,前面六个字符"ABCDAB"是匹配的。查表可知,最后一个匹配字符B对应的"部分匹配值"为2,因此按照下面的公式算出向后移动的位数:
移动位数 = 已匹配的字符数 - 对应的部分匹配值
因为 6 - 2 等于4,所以将搜索词向后移动4位。
2.移动后如下,将c和对比:

因为空格与C不匹配,搜索词还要继续往后移。这时,已匹配的字符数为2(“AB”),对应的"部分匹配值"为0。所以,移动位数 = 2 - 0,结果为 2,于是将搜索词向后移2位。
3.移动后,又将A和对比:
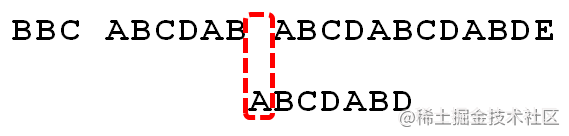
因为空格与A不匹配,继续后移一位。
4.再次移动后,又需要重新对比ABCDABD

逐位比较,直到发现C与D不匹配。于是,移动位数 = 6 - 2,继续将搜索词向后移动4位。
5.再次移动后从CDABD开始继续逐位比较,直到搜索词的最后一位,发现完全匹配,于是搜索完成。如果还要继续搜索(即找出全部匹配),移动位数 = 7 - 0,再将搜索词向后移动7位,这里就不再重复了。
 \
\
2.2.2.2 KMP算法的代码
理解了实例过后,我们就可以看代码了。
先看伪代码:
KMP-MATCHER(T, P)
n ← length[T]
m ← length[P]
π ← COMPUTE-PREFIX-FUNCTION(P)
q ← 0 //Number of characters matched.
for i ← 1 to n //Scan the text from left to right.do while q > 0 and P[q + 1] ≠ T[i]do q ← π[q] //Next character does not match.if P[q + 1] = T[i]then q ← q + 1 //Next character matches.if q = m //Is all of P matched?then print "Pattern occurs with shift" i - mq ← π[q] //Look for the next match.
C++实现:
// C++ program for implementation of KMP pattern searching
// algorithm
#include <bits/stdc++.h>void computeLPSArray(char* pat, int M, int* lps);// Prints occurrences of txt[] in pat[]
void KMPSearch(char* pat, char* txt)
{int M = strlen(pat);int N = strlen(txt);// create lps[] that will hold the longest prefix suffix// values for patternint lps[M];// Preprocess the pattern (calculate lps[] array)computeLPSArray(pat, M, lps);int i = 0; // index for txt[]int j = 0; // index for pat[]while (i < N) {if (pat[j] == txt[i]) {j++;i++;}if (j == M) {printf("Found pattern at index %d ", i - j);j = lps[j - 1];}// mismatch after j matcheselse if (i < N && pat[j] != txt[i]) {// Do not match lps[0..lps[j-1]] characters,// they will match anywayif (j != 0)j = lps[j - 1];elsei = i + 1;}}
}// Fills lps[] for given patttern pat[0..M-1]
void computeLPSArray(char* pat, int M, int* lps)
{// length of the previous longest prefix suffixint len = 0;lps[0] = 0; // lps[0] is always 0// the loop calculates lps[i] for i = 1 to M-1int i = 1;while (i < M) {if (pat[i] == pat[len]) {len++;lps[i] = len;i++;}else // (pat[i] != pat[len]){// This is tricky. Consider the example.// AAACAAAA and i = 7. The idea is similar// to search step.if (len != 0) {len = lps[len - 1];// Also, note that we do not increment// i here}else // if (len == 0){lps[i] = 0;i++;}}}
}// Driver program to test above function
int main()
{char txt[] = "ABABDABACDABABCABAB";char pat[] = "ABABCABAB";KMPSearch(pat, txt);return 0;
}其他的数据结构与算法的相关内容,我会继续更新在这个专栏,欢迎收藏。