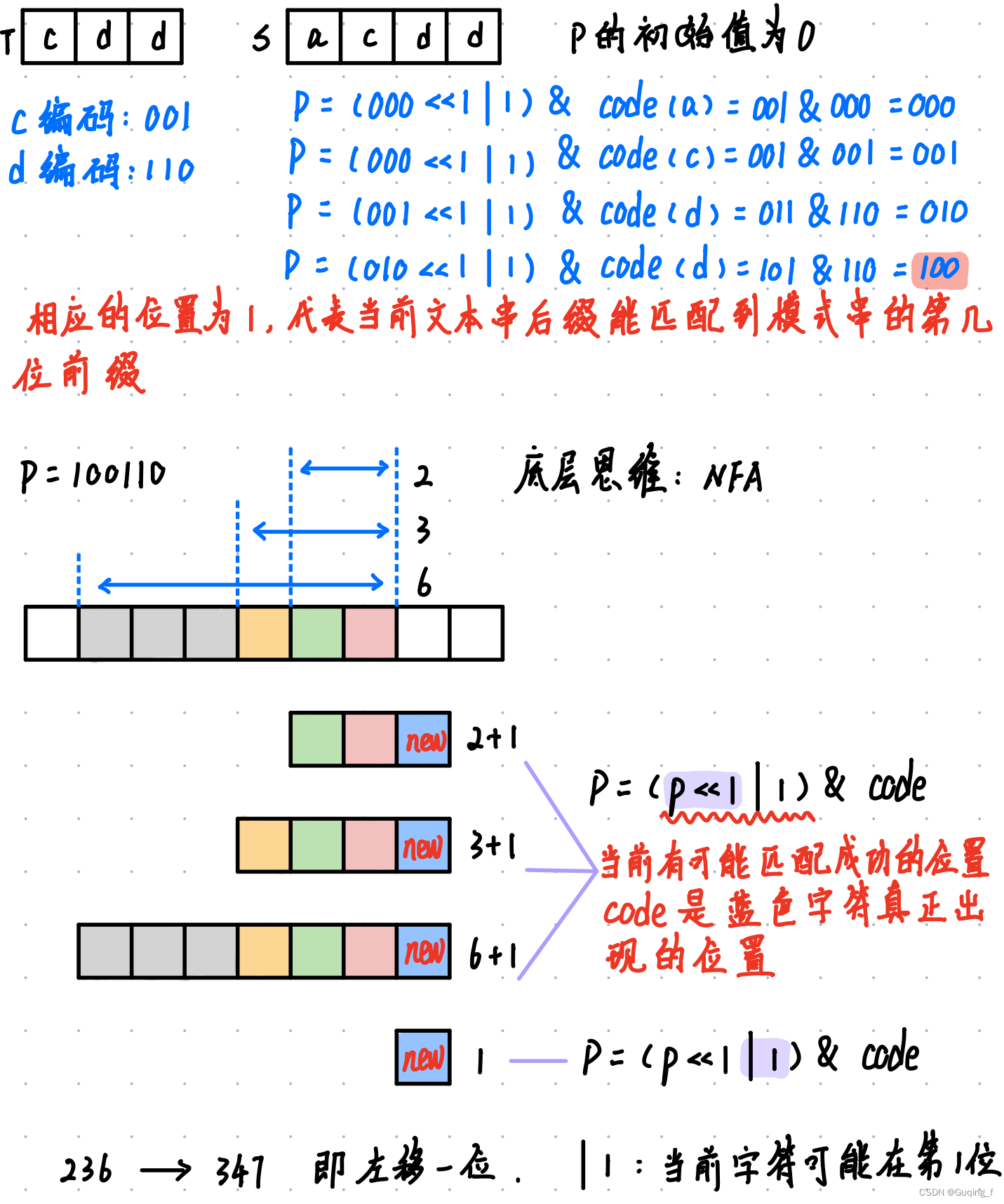
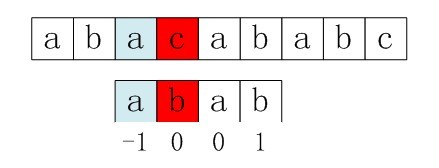
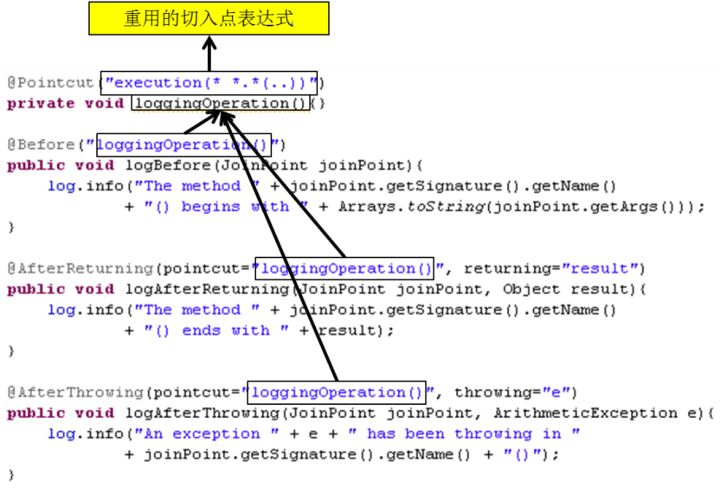
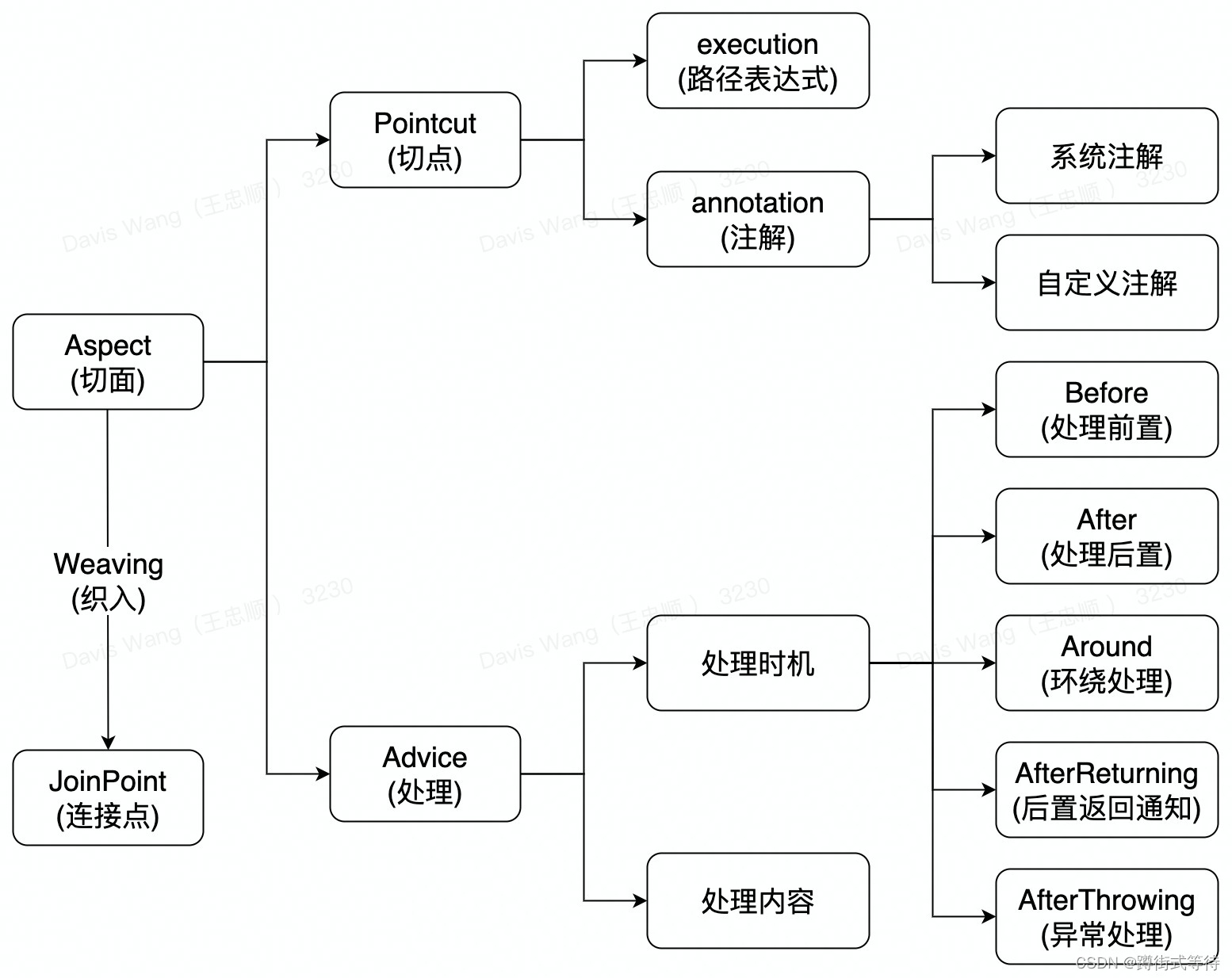
字符串匹配：设 S 和 T 是给定的两个串，在主串 S 中找到模式串 T 的过程称为字符串匹配，如果在主串 S 中找到模式串 T ，则称匹配成功，函数返回 T 在 S 中首次出现的位置，否则匹配不成功，返回 -1。
例：

在上图中，我们试图找到模式串 T = baab,在主串 S = abcabaabcabac 中第一次出现的位置，即为红色阴影部分， T 第一次在 S 中出现的位置下标为 4 （ 字符串的首位下标是 0 ），所以返回 4。如果模式串 T 没有在主串 S 中出现，则返回 -1。

leedcode第28题 ：找出字符串中第一个匹配项的下标
给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标（下标从 0 开始）。如果 needle 不是 haystack 的一部分，则返回 -1 。
示例一

输入：haystack = “sadbutsad”, needle = “sad” 输出：0 解释：“sad” 在下标 0 和 6 处匹配。
第一个匹配项的下标是 0 ，所以返回 0 。

示例二

输入：haystack = “leetcode”, needle = “leeto” 输出：-1 解释：“leeto” 没有在
“leetcode” 中出现，所以返回 -1 。

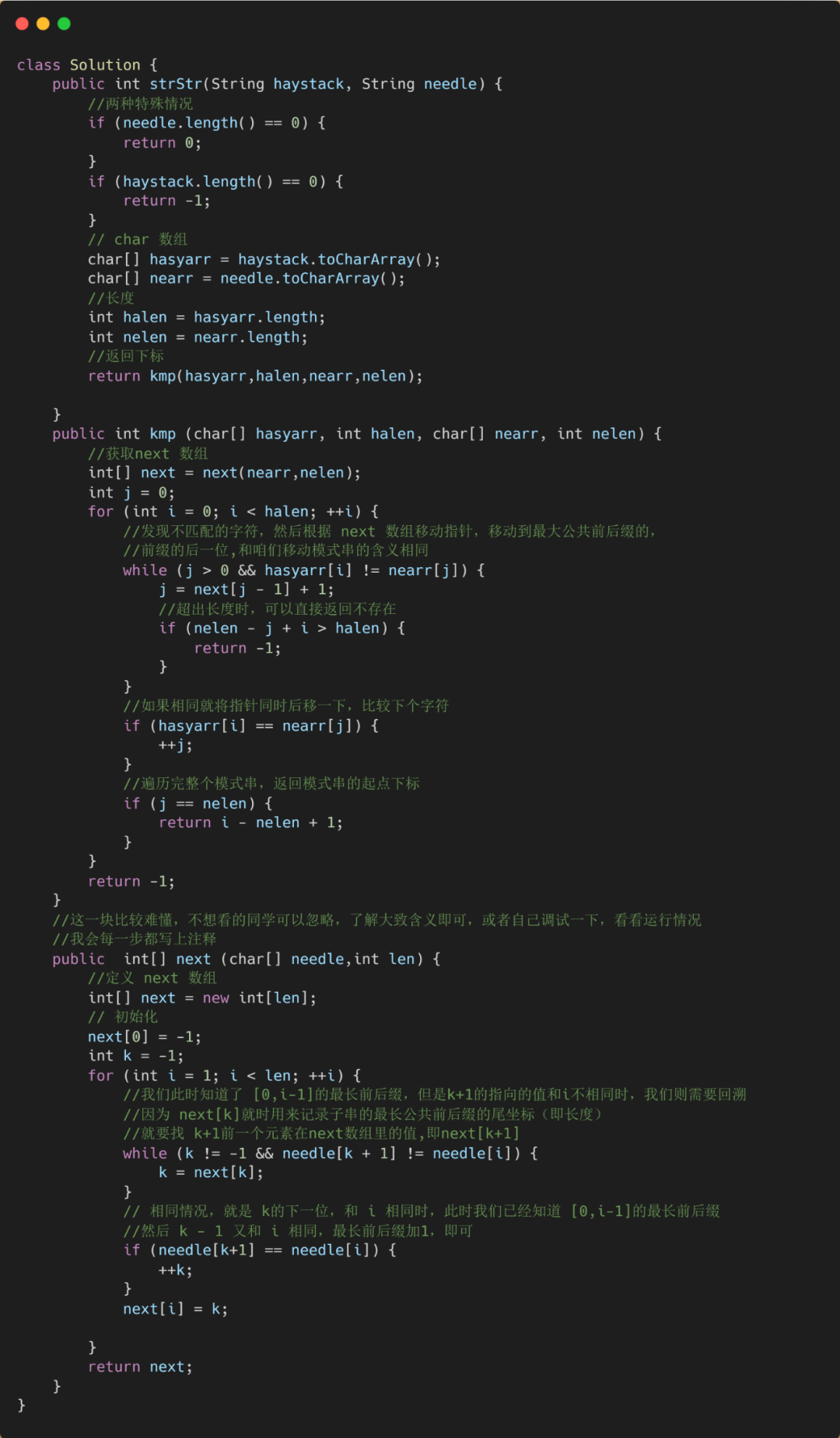
方法一、暴力匹配算法

class Solution {  //方法一，暴力算法public int strStr(String haystack, String needle) {//获取主串和模式串的长度int haystackLength=haystack.length();int needleLength=needle.length();//排除一些特殊情况if(needleLength==0){//当模式串的长度为0return -1;}if(haystackLength<needleLength){//当模式串的长度大于主串return -1;}//我们主串比较的指针最后就是haystackLength-needleLength//因为我们需要比较的字符串长度是needleLength，减去后，当循环到最后一个//此时字符串末尾的字符串个数就是needleLength的个数，相当于是最后一次进行比较//如果主串的指针继续移动的话，那么就不是完整的比较模式串了for(int i=0;i<=haystackLength-needleLength;i++){//将j提出来用于下面的判断int j;//判断是否匹配成功for(j=0;j<needleLength;j++){//将模式串的每一个字符和主串对应的字符进行匹配，如果匹配不成功则结束当前这个for循环if(haystack.charAt(i+j)!=needle.charAt(j)){break;}}//如果能走到这里，j的长度等于模式串的长度，说明匹配成功，返回所在下标if(j==needleLength){return i;}}return -1;}
}

方法二、BF算法（Brute Force）

这个算法很容易理解，其实原理和暴力匹配一样，就是对代码进行了一下修改，就是我们将模式串和主串进行比较，一致时则继续比较下一字符，直到比较完整个模式串。不一致时则将主串后移一位，重新从模式串的首位开始对比

class Solution {//BF算法public int strStr(String haystack, String needle) {//i代表主串指针，j代表模式串指针int i,j;//主创长度和模式串长度int halen=haystack.length();int nelen=needle.length();//循环条件，这里只有i在增长//当i遍历完主串或者j遍历完模式串，不满足循环条件，结束循环for(i=0,j=0;i<halen&&j<nelen;i++){//相同时则移动j指针if(haystack.charAt(i)==needle.charAt(j)){j++;}else{//如果不同则将i指针指向原来的位置(后面因为会i++所以相当于指向原来的下一个位置)，j指针重新指向头位置，重新进行匹配。i=i-j;j=0;}}if(j==nelen){return i-nelen;}else{return -1;}}}

方法三、BM算法（Boyer－Moore）

BM算法有两大规则：坏字符规则和好后缀规则
坏字符规则：

光有坏字符是不够的！因为坏字符可能会出bug，让你后退着滑动…
如下图

好后缀规则
鉴于坏字符规则可能出现的“倒滑”问题，我们需要好后缀规则
好后缀规则分为两部分——好后缀全匹配规则和好后缀的后缀子串全匹配模串前缀子串规则
首先，我们要知道什么叫好后缀，好后缀就是坏字符后面的那一串后缀字符串。
如下图

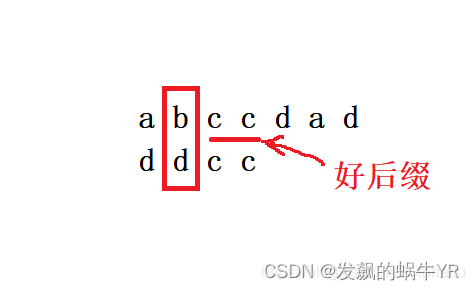
（1）好后缀全匹配规则
好后缀全匹配规则与坏字符规则有些类似，但是他匹配的是整个后缀字符串。
如下图

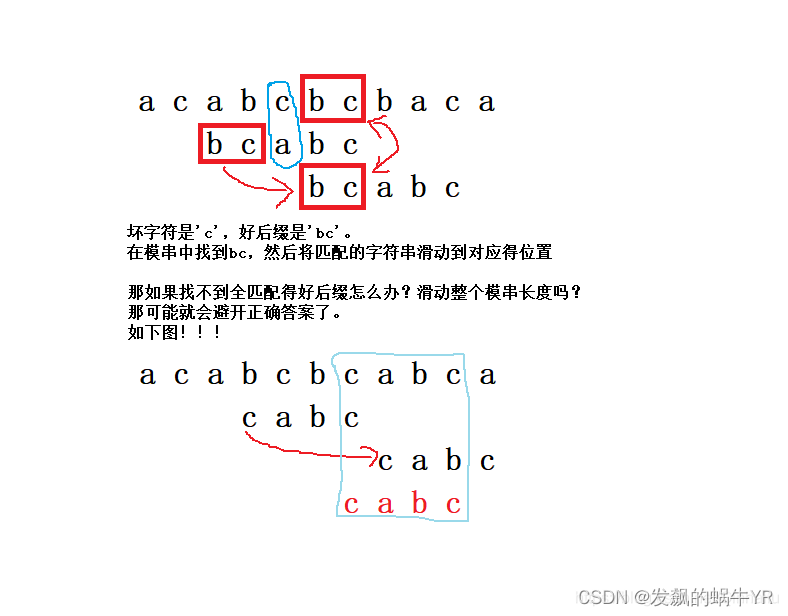
（2）好后缀的后缀子串匹配模串前缀子串规则
正因为可能因为找不到全匹配得好后缀导致得滑动过多，所以我们需要“好后缀的后缀子串匹配模串前缀子串规则”。
如下图

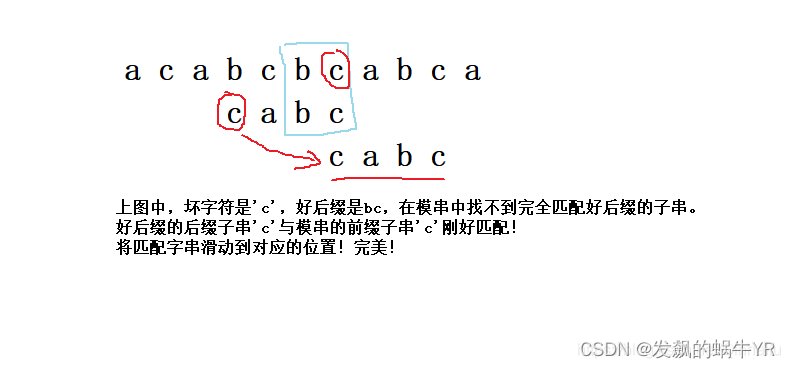
BM算法完整代码：

// a,b表示主串和模式串；n，m表示主串和模式串的长度。
public int bm(char[] a, int n, char[] b, int m) {int[] bc = new int[SIZE]; // 记录模式串中每个字符最后出现的位置generateBC(b, m, bc); // 构建坏字符哈希表int[] suffix = new int[m];boolean[] prefix = new boolean[m];generateGS(b, m, suffix, prefix);int i = 0; // j表示主串与模式串匹配的第一个字符while (i <= n - m) {int j;for (j = m - 1; j >= 0; --j) { // 模式串从后往前匹配if (a[i+j] != b[j]) break; // 坏字符对应模式串中的下标是j}if (j < 0) {return i; // 匹配成功，返回主串与模式串第一个匹配的字符的位置}int x = j - bc[(int)a[i+j]];int y = 0;if (j < m-1) { // 如果有好后缀的话y = moveByGS(j, m, suffix, prefix);}//好后缀和坏字符中最长的i = i + Math.max(x, y);}return -1;
}// j表示坏字符对应的模式串中的字符下标; m表示模式串长度
private int moveByGS(int j, int m, int[] suffix, boolean[] prefix) {int k = m - 1 - j; // 好后缀长度if (suffix[k] != -1) return j - suffix[k] +1;for (int r = j+2; r <= m-1; ++r) {if (prefix[m-r] == true) {return r;}}return m;
}

方法四、KMP算法

KMP的经典思想就是:当出现字符串不匹配时，可以记录一部分之前已经匹配的文本内容，利用这些信息避免从头再去做匹配。
什么是kmp,kmp有什么用？
因为是由这三位学者发明的：Knuth，Morris和Pratt，所以取了三位学者名字的首字母。所以叫做KMP。KMP主要应用在字符串匹配上。
前缀表(prefix table)
一般写kmp都是需要一个next数组，而这个next数组其实就是一个前缀表。
那么前缀表有什么用呢？
前缀表是用来回退的，它记录了模式串与主串(文本串)不匹配的时候，模式串应该从哪里开始重新匹配。
为了清楚的了解前缀表的来历，我们举个例子：
要在文本串：aabaabaafa 中查找是否出现过一个模式串：aabaaf。

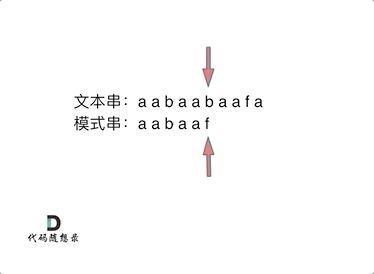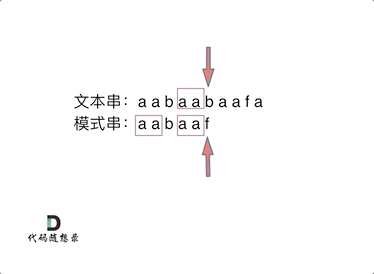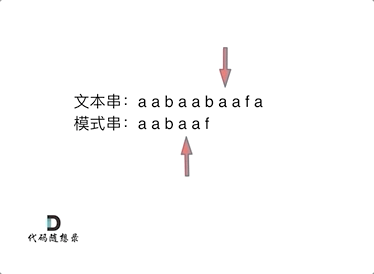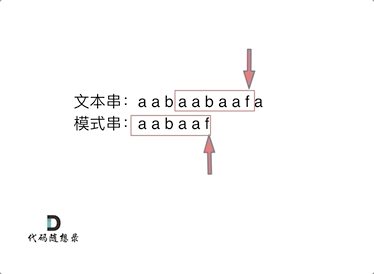
动画里，特意把 子串aa 标记上了，这是有原因的，大家先注意一下，后面还会说道。
可以看出，文本串中第六个字符b 和 模式串的第六个字符f，不匹配了。如果使用暴力匹配，会发现不匹配，此时模式串就要从头匹配了。
但如果使用前缀表，就不会从头匹配，而是从上次已经匹配的内容开始匹配，找到了模式串中第三个字符b继续开始匹配。
那么前缀表是如何记录的呢？
首先要知道前缀表的任务是当前位置匹配失败，找到之前已经匹配上的位置，再重新匹配，此也意味着在某个字符失配时，前缀表会告诉你下一步匹配中，模式串应该跳到哪个位置。
那么什么是前缀表：记录下标i之前（包括i）的字符串中，有多大长度的相同前缀后缀。

最长相等前后缀

前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串。
后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。
前缀表要求的就是相同前后缀的长度。
所以字符串a的最长相等前后缀为0。 字符串aa的最长相等前后缀为1。 字符串aaa的最长相等前后缀为2，字符串aab的最长相等前后缀为0，字符串aaba的最长相等前后缀为1，字符串aabaa的最长相等前后缀为2，字符串aabaaf的最长相等前后缀为0。

为什么使用前缀表

回顾一下，刚刚匹配的过程在下标5的地方遇到不匹配，模式串是指向f，如图：

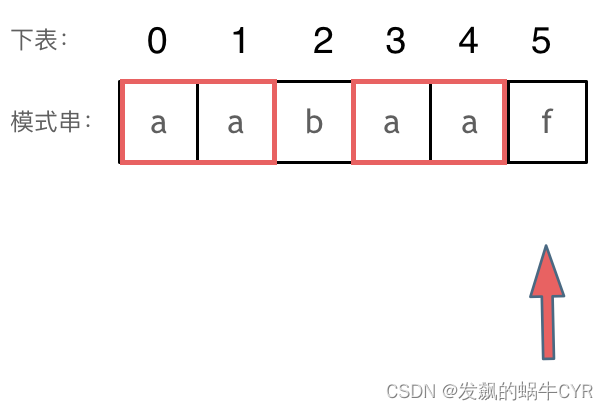
然后就找到了下标2，指向b，继续匹配：如图：

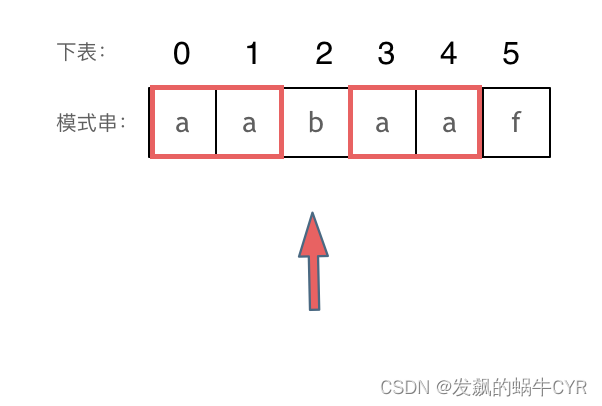
下标5之前这部分的字符串（也就是字符串aabaa）的最长相等的前缀 和 后缀字符串是 子字符串aa ，因为找到了最长相等的前缀和后缀，匹配失败的位置是后缀子串的后面，那么我们找到与其相同的前缀的后面从新匹配就可以了。

所以前缀表具有告诉我们当前位置匹配失败，跳到之前已经匹配过的地方的能力。

如何计算前缀表

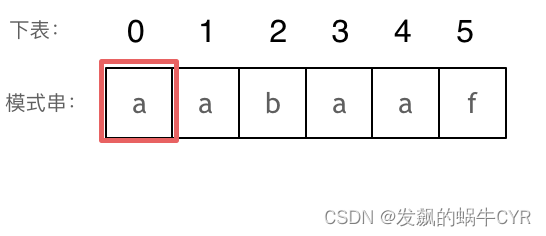
长度为前1个字符的子串a，最长相同前后缀的长度为0。（注意字符串的前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串；后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。）

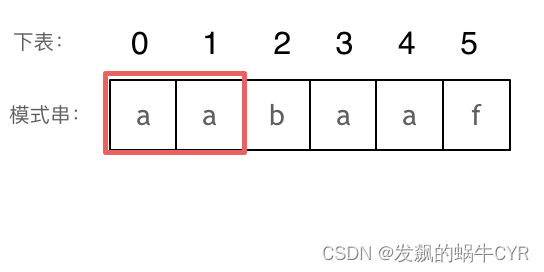
长度为前2个字符的子串aa，最长相同前后缀的长度为1。

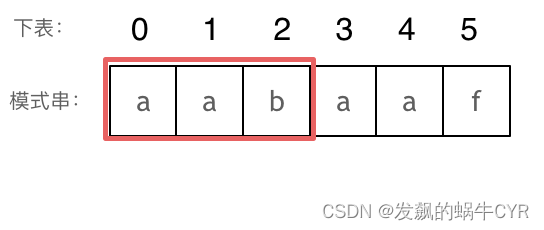
长度为前3个字符的子串aab，最长相同前后缀的长度为0。

以此类推： 长度为前4个字符的子串aaba，最长相同前后缀的长度为1。 长度为前5个字符的子串aabaa，最长相同前后缀的长度为2。 长度为前6个字符的子串aabaaf，最长相同前后缀的长度为0。

那么把求得的最长相同前后缀的长度就是对应前缀表的元素，如图：

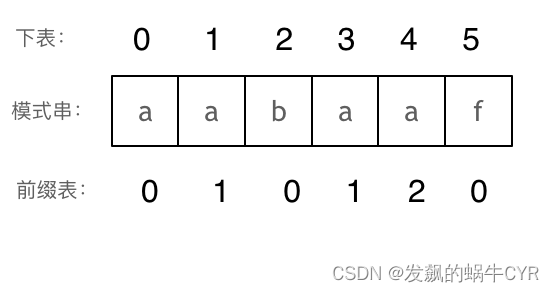
可以看出模式串与前缀表对应位置的数字表示的就是：下标i之前（包括i）的字符串中，有多大长度的相同前缀后缀。

再来看一下如何利用 前缀表找到 当字符不匹配的时候应该指针应该移动的位置。(前缀表不减一)如动画所示：

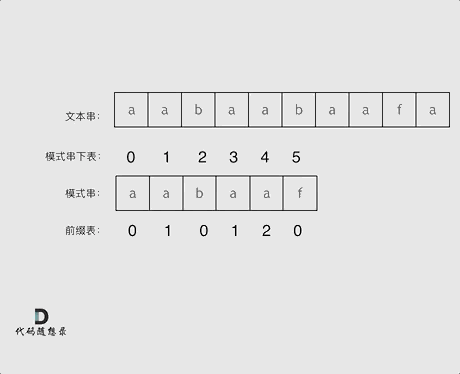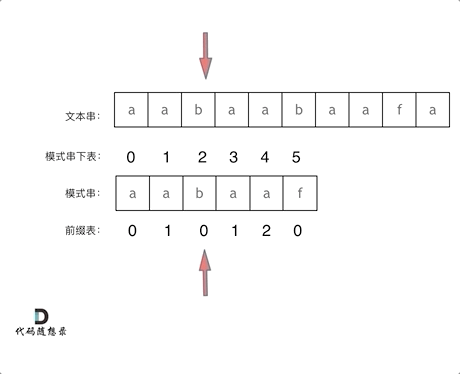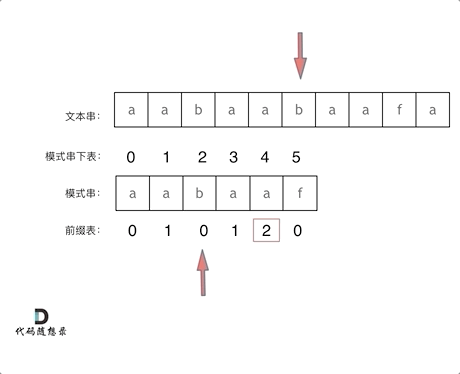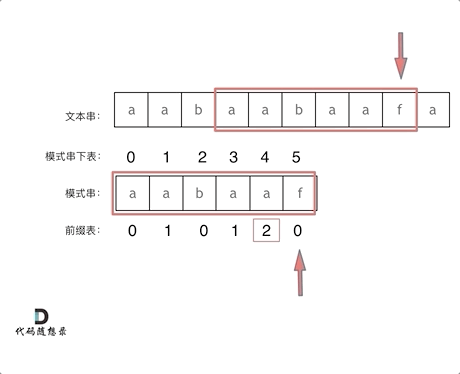
找到的不匹配的位置， 那么此时我们要看它的前一个字符的前缀表的数值是多少。

为什么要前一个字符的前缀表的数值呢，因为要找前面字符串的最长相同的前缀和后缀。

所以要看前一位的 前缀表的数值。

前一个字符的前缀表的数值是2， 所有把下标移动到下标2的位置继续比配。

前缀表与next数组

很多KMP算法的时间都是使用next数组来做回退操作，next数组就可以是前缀表，但是很多实现都是把前缀表统一减一（右移一位，初始位置为-1）之后作为next数组。
其实这并不涉及到KMP的原理，而是具体实现，next数组即可以就是前缀表，也可以是前缀表统一减一（右移一位，初始位置为-1）。
使用next数组来进行匹配(前缀表统一减一)

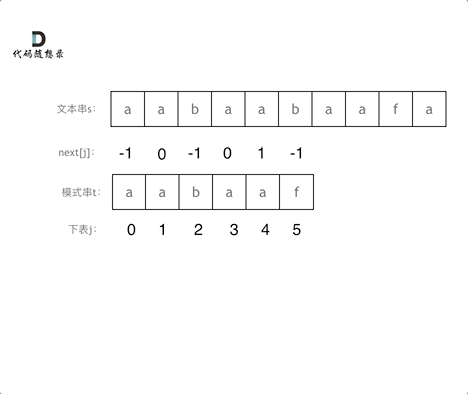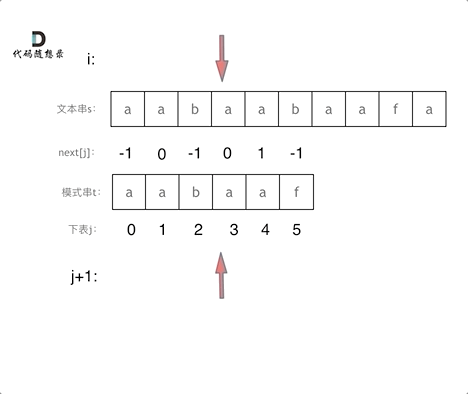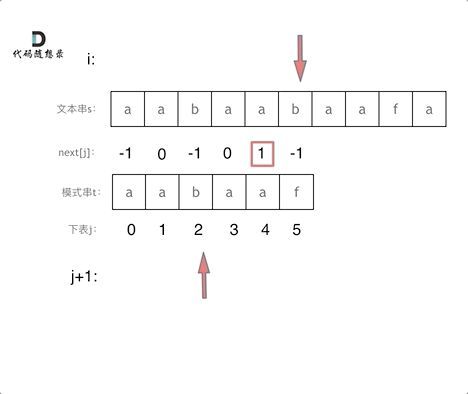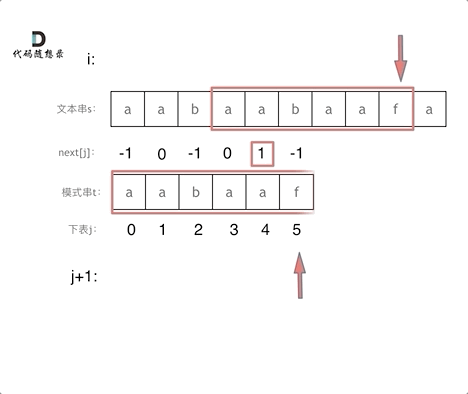
时间复杂度分析

其中n为文本串长度，m为模式串长度，因为在匹配的过程中，根据前缀表不断调整匹配的位置，可以看出匹配的过程是O(n)，之前还要单独生成next数组，时间复杂度是O(m)。所以整个KMP算法的时间复杂度是O(n+m)的。

暴力的解法显而易见是O(n × m)，所以KMP在字符串匹配中极大的提高的搜索的效率。

构造next数组

都知道使用kmp，一定要构建next数组
我们定义一个函数getNext来构建next数组

public void getNext(int[] next, String s)

构造next数组其实就是计算模式串s，前缀表的过程。
主要有如下三步：
1.初始化
2.处理前后缀不相同的情况
3.处理前后缀相同的情况
初始化
定义两个指针i和j，j指向前缀末尾位置，i指向后缀末尾位置。
然后还要对next数组进行初始化赋值，如下：

int j = -1;
next[0] = j;

j 为什么要初始化为 -1呢，因为之前说过 前缀表要统一减一的操作仅仅是其中的一种实现，我们这里选择j初始化为-1，下文还会给出j不初始化为-1的实现代码。
next[i] 表示 i之前最长相等的前后缀长度（其实就是j），例如子串为aabaaf，如果i指向f，则j此时应该就是子串aabaa，也就是i之前的最长相等前后缀长度(最长相等前后缀，前缀和后缀长度是一样的)
所以初始化next[0] = j 。
处理前后缀不相同的情况
因为j初始化为-1，那么i就从1开始，进行s[i] 与 s[j+1]的比较。
所以遍历模式串s的循环下标i 要从 1开始，代码如下：

for (int i = 1; i < s.size(); i++) {

如果 s[i] 与 s[j+1]不相同，也就是遇到 前后缀末尾不相同的情况，就要向前回退。
怎么回退呢？
next[j]就是记录着j之前的子串的相同前后缀的长度。
那么 s[i] 与 s[j+1] 不相同，就要找 j+1前一个元素在next数组里的值（就是next[j]）。
所以，处理前后缀不相同的情况代码如下：

while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了j = next[j]; // 向前回退
}

处理前后缀相同的情况
如果 s[i] 与 s[j + 1] 相同，那么就同时向后移动i 和j 说明找到了相同的前后缀，同时还要将j（前缀的长度）赋给next[i], 因为next[i]要记录相同前后缀的长度。代码如下：

if (s[i] == s[j + 1]) { // 找到相同的前后缀j++;
}
next[i] = j;

使用next数组进行匹配

在文本串s里 找是否出现过模式串t。
定义两个下标j 指向模式串起始位置，i指向文本串起始位置。
那么j初始值依然为-1，为什么呢？ 依然因为next数组里记录的起始位置为-1。
i就从0开始，遍历文本串，代码如下：

for (int i = 0; i < s.size(); i++) 

接下来就是 s[i] 与 t[j + 1] （因为j从-1开始的） 进行比较。
如果 s[i] 与 t[j + 1] 不相同，j就要从next数组里寻找下一个匹配的位置。
代码如下：

while(j >= 0 && s[i] != t[j + 1]) {j = next[j];
}

如果 s[i] 与 t[j + 1] 相同，那么i 和 j 同时向后移动， 代码如下：

if (s[i] == t[j + 1]) {j++; // i的增加在for循环里
}

如何判断在文本串s里出现了模式串t呢，如果j指向了模式串t的末尾，那么就说明模式串t完全匹配文本串s里的某个子串了。
本题要在文本串字符串中找出模式串出现的第一个位置 (从0开始)，所以返回当前在文本串匹配模式串的位置i 减去 模式串的长度，就是文本串字符串中出现模式串的第一个位置。
代码如下：

if (j == (t.size() - 1) ) {return (i - t.size() + 1);
}

最后的整体代码（前缀表统一减一）

class Solution {public void getNext(int[] next, String s){int j = -1;next[0] = j;for (int i = 1; i<s.length(); i++){while(j>=0 && s.charAt(i) != s.charAt(j+1)){j=next[j];}if(s.charAt(i)==s.charAt(j+1)){j++;}next[i] = j;}}public int strStr(String haystack, String needle) {if(needle.length()==0){return 0;}int[] next = new int[needle.length()];getNext(next, needle);int j = -1;for(int i = 0; i<haystack.length();i++){while(j>=0 && haystack.charAt(i) != needle.charAt(j+1)){j = next[j];}if(haystack.charAt(i)==needle.charAt(j+1)){j++;}if(j==needle.length()-1){return (i-needle.length()+1);}}return -1;}
}

前缀表不减一代码

class Solution {//前缀表(不减一)public int strStr(String haystack, String needle) {if(needle.length()==0){return 0;}int[] next=new int[needle.length()];getNext(next,needle);//通过next数组，实现模式串和主串的匹配//因为next数组记录的起始位置为0int j=0;//i代表主串，从第0个位置开始匹配，初始位置是0for(int i=0;i<haystack.length();i++){//不匹配while(j>0&&needle.charAt(j)!=haystack.charAt(i)){//j寻找之前的匹配位置j=next[j-1];}//匹配，j和i同时向右移动，j在for循环里移动if(needle.charAt(j)==haystack.charAt(i)){j++;}//主串中出现模式串if(j==needle.length()){//haystack串里出现needle串 return i-needle.length()+1;}}return -1;}//定义两个指针i和j，j指向前缀末尾位置，i指向后缀末尾位置。private void getNext(int[] next,String s){//初始化j指针为0，因为前缀的首个就是从0开始int j=0;//初始化next数组的值是0，因为当只有一个字符的字符串，相同前后缀的最大长度是0next[0]=0;//初始化i指针为1，因为当i从1开始，这样i和j才能进行比较，例如//a a b a a f//i j //i和j的初始位置for(int i=1;i<s.length();i++){//如果前后缀不同，则不匹配，则需要看前一位的位置才知道要跳到哪里//因为当j=0也回退到了初始值的位置，没有必要再回退，且next[0-1]会数组越界//所以j要大于0while(j>0&&s.charAt(j)!=s.charAt(i)){//向前回退//那么 s[i] 与 s[j] 不相同，就要找 j前一个元素在next数组里的值j=next[j-1];}//如果 s[i] 与 s[j] 相同，那么就同时向后移动i 和j 说明找到了相同的前后缀，同时还要将j（前缀的长度）赋给next[i], 因为next[i]要记录相同前后缀的长度。if(s.charAt(j)==s.charAt(i)){//如果相等则继续向右移动j指针，同时执行完，i指针也会向右移动j++;//更新数组next[i]=j;}}   }
}