问题：

       给你两个字符串  s 和 pat ，请你在 s 字符串中找出 pat 字符串出现的第一个位置（下标从 0 开始），如果不存在则返回-1。

1.暴力匹配算法。

          暴力匹配算法较好理解，其大致原理如图：

         

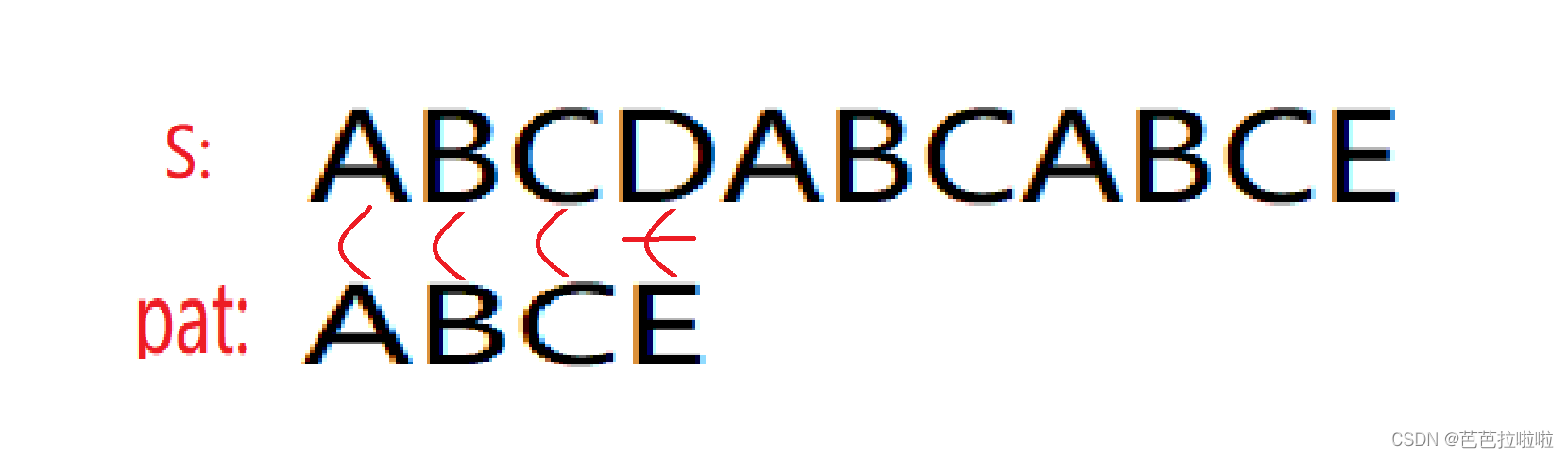
          当D和E不匹配的时候，pat模式串会向右移动一位，然后继续匹配。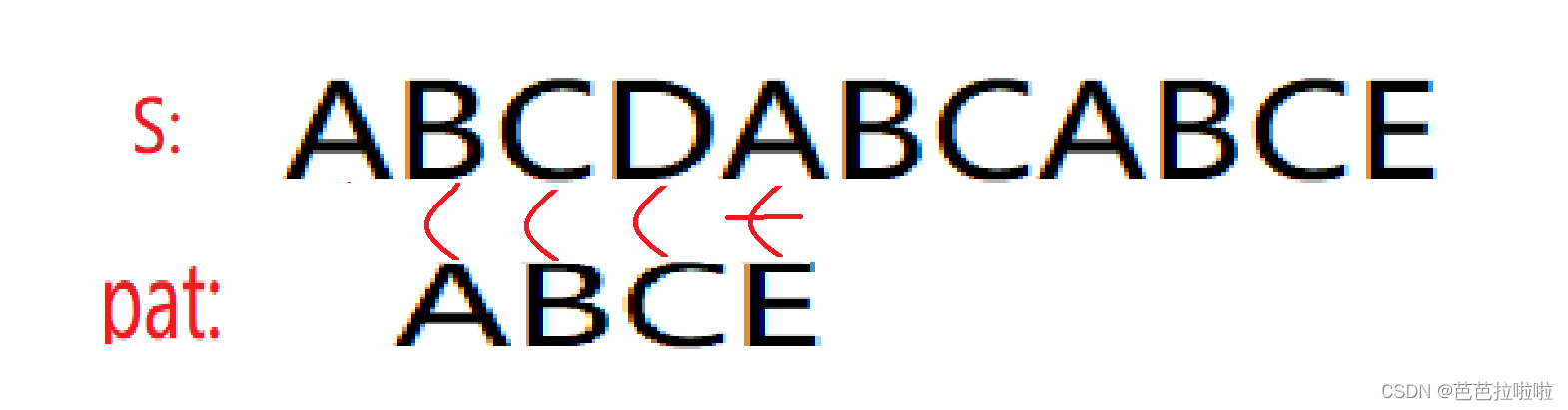 

         一直这样匹配，直到匹配到模式串或者匹配不成功为止。

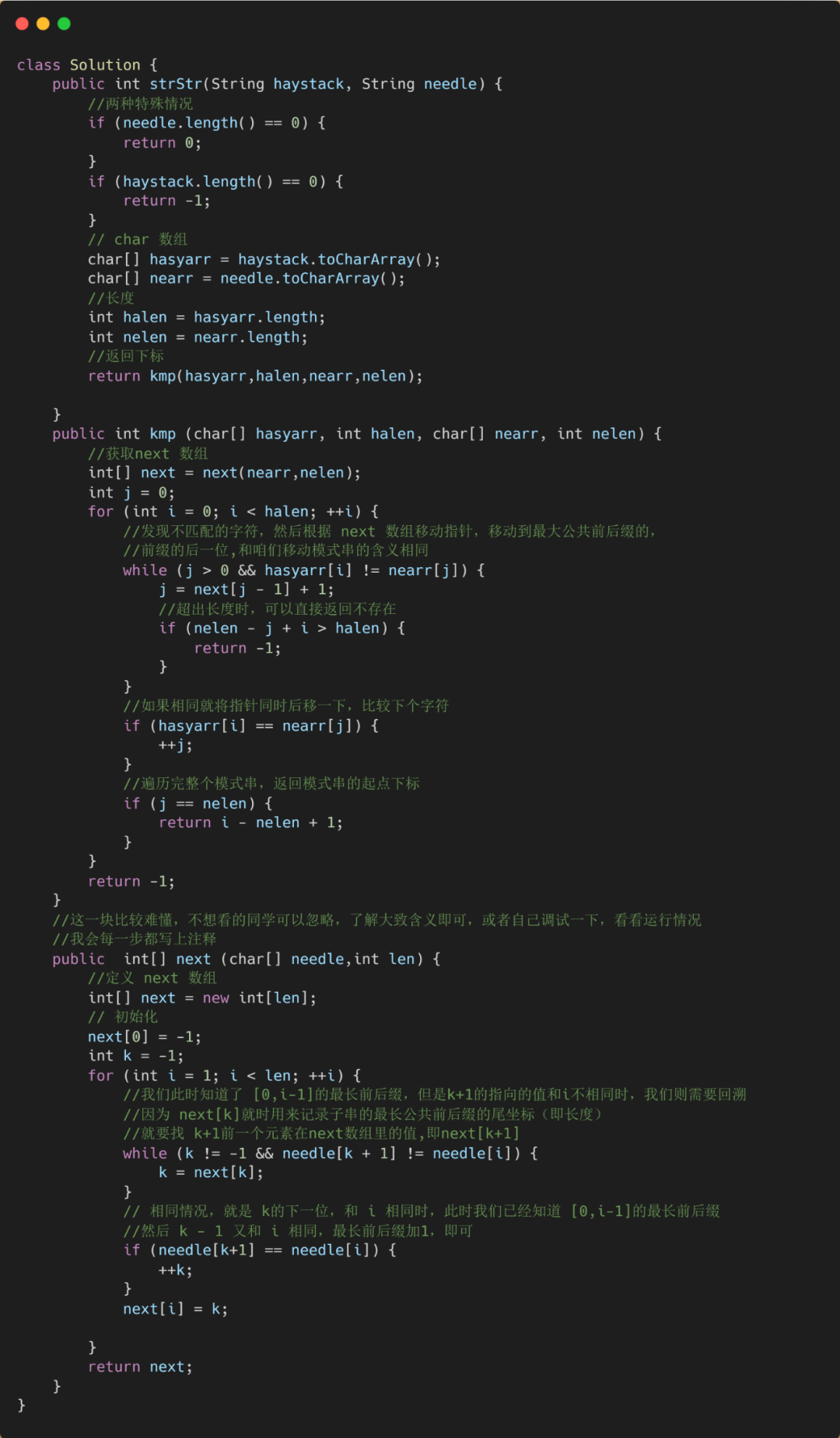
代码如下：

class Solution {public static int strStr(String s , String pat){for (int i = 0 ; i <= s.length() - pat.length() ; i++){int m = i;for(int n = 0 ; n < pat.length() ; n++){if(s.charAt(m) != pat.charAt(n)){break;}if(n == pat.length()-1){return i;}m++; }}return -1;}
}

2.KMP算法。

        KMP的优势在于它能够利用字符串匹配失败后的信息对下次匹配进行优化，而不是每次都

傻傻的对下一个字符进行匹配。

        但是如何利用匹配失败后的有效信息呢？

 如图：

         

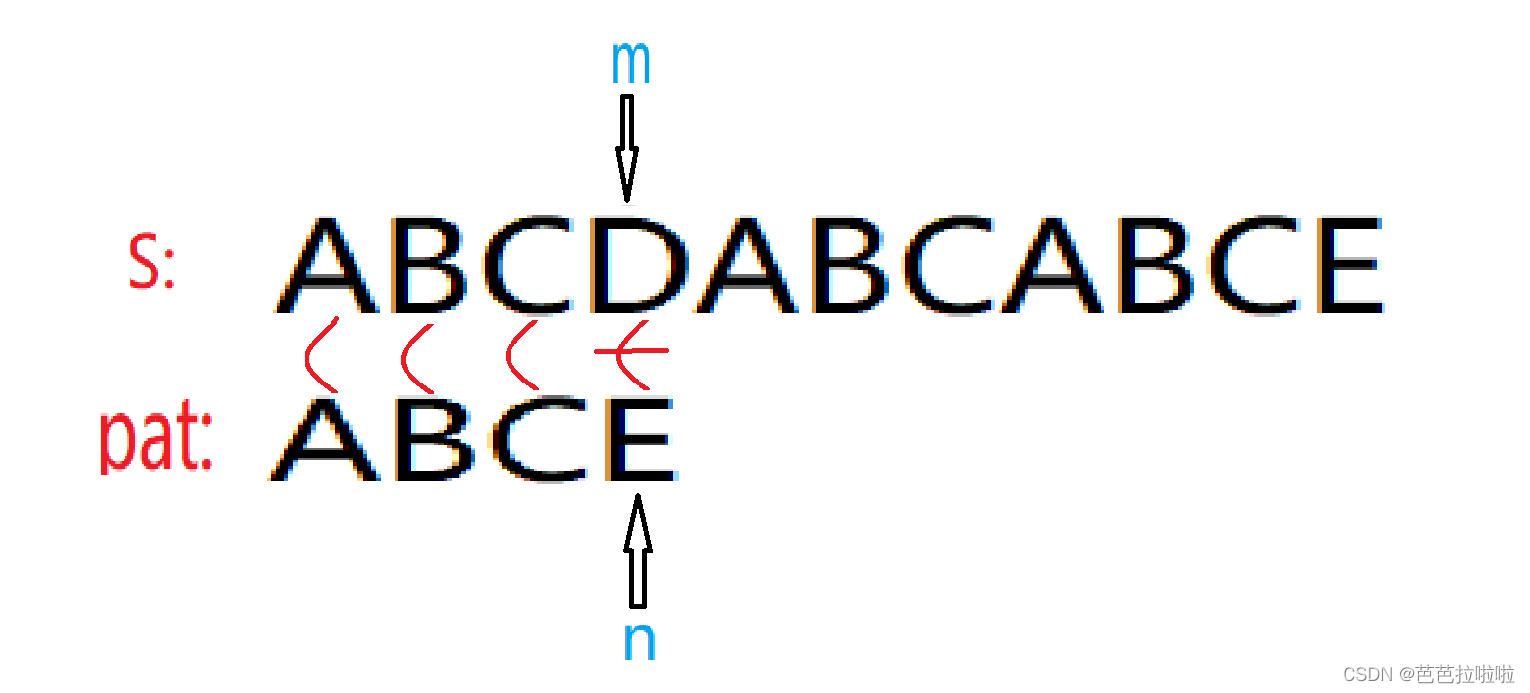
         我们暂且用m指针指向字符串s匹配到的位置，用n指针来表示模式串pat匹配到的位置。

当我们匹配到第n个字符匹配失败时，说明模式串的前n-1个字符至少是匹配成功的。

        而这相同的前n-1个字符，就是我们在匹配失败后所掌握的信息。

        我们来看下面这种情况：

        

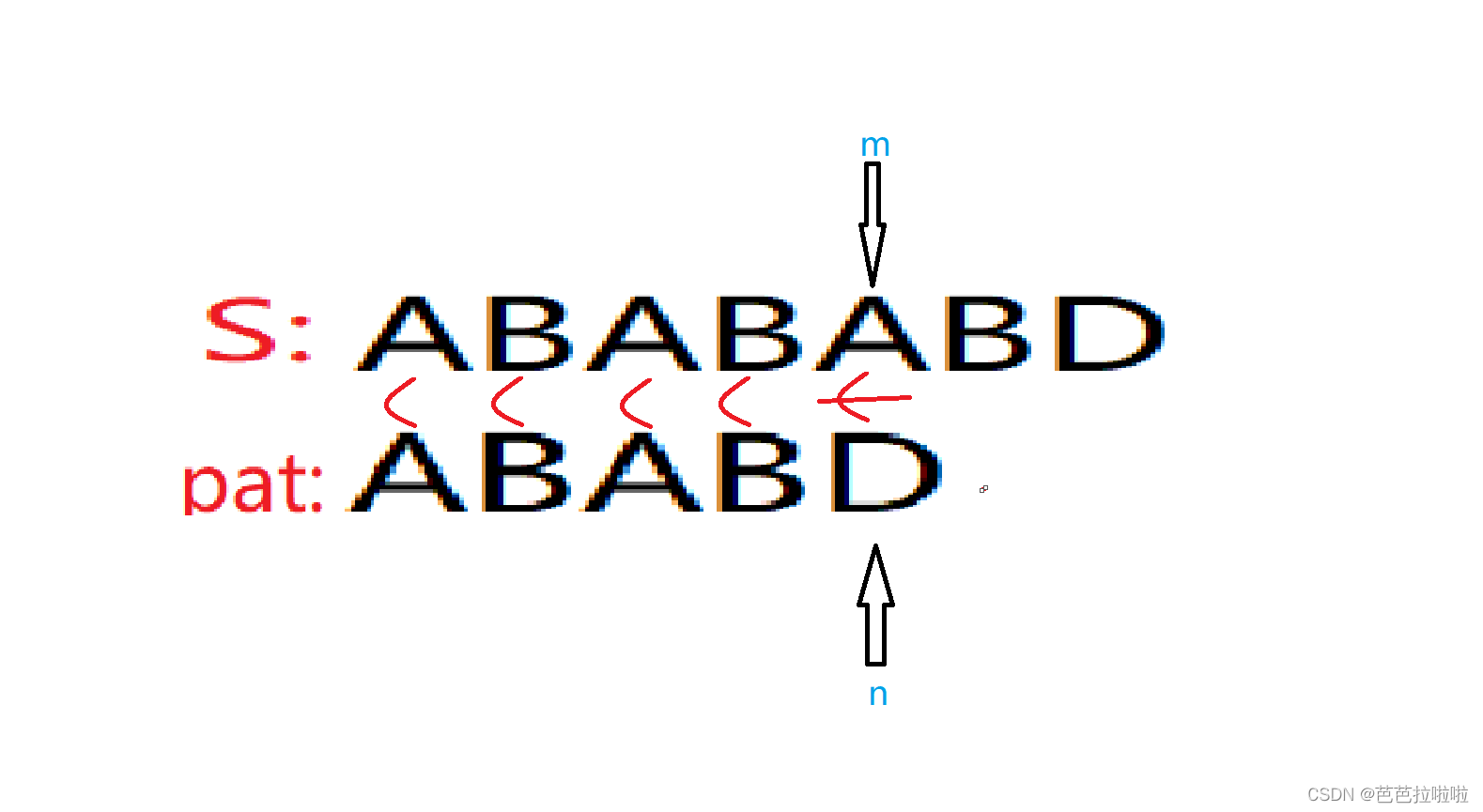
当 S[m] 与 pat[n] 匹配失败时，如何利用匹配失败的信息？ 

当匹配失败时，我们可以确定的是pat模式串的前 (n-1)个字符与S字符串的前 (n-1)个字符是相同的。

这就是我们可以利用的信息。这样就相当于我们事先知道了要匹配的字符！！！

       

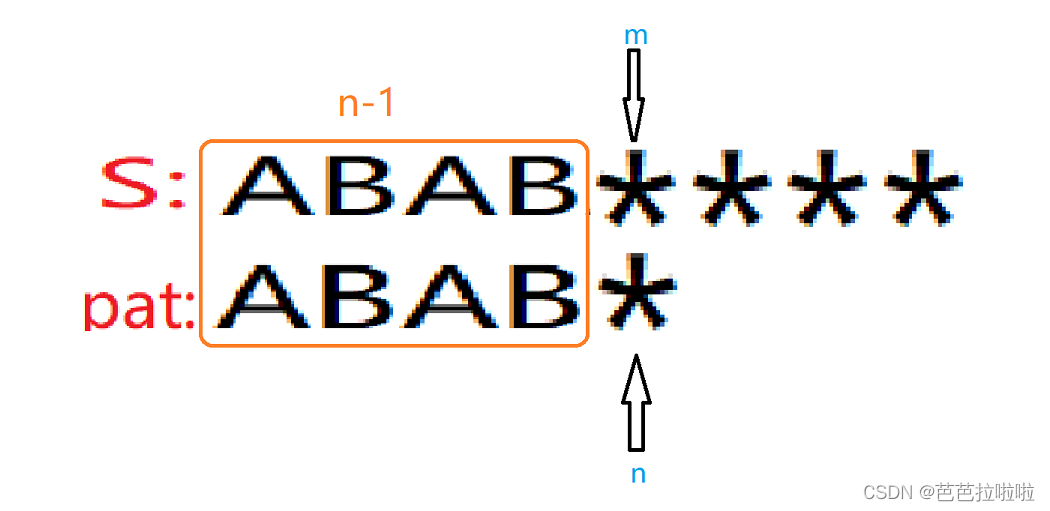
       既然我们知道了S与pat串的前n-1个字符相同，我们就不用每次都让m指针回退至第二个字符处，m指针可以不动，只让n指针指向它应该指向的位置（如果pat模式串从第一位就不匹配，我们需要让m指针后退一位）。

如图：

        

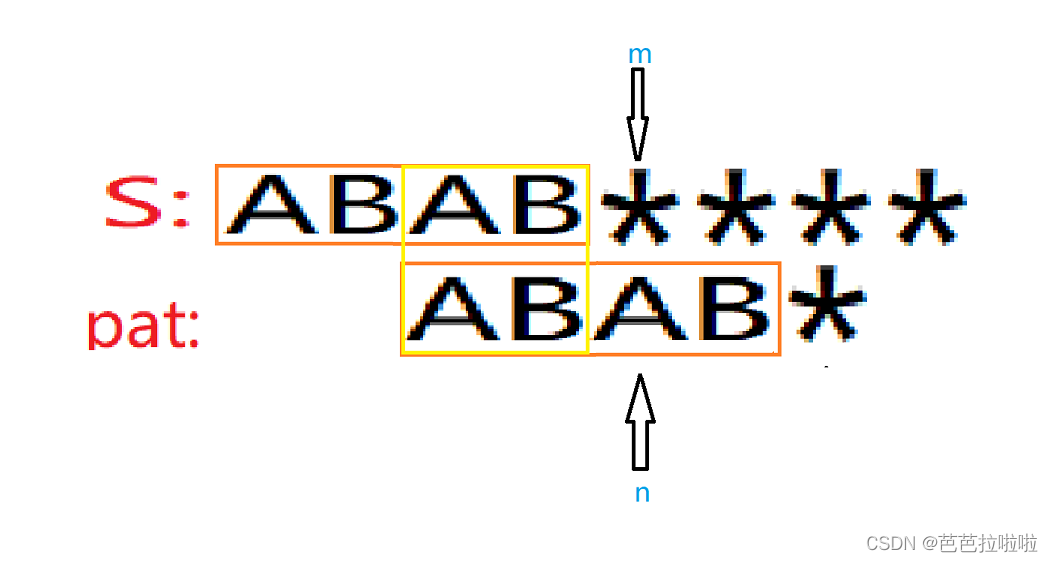
那么n指针应该指向哪里呢？

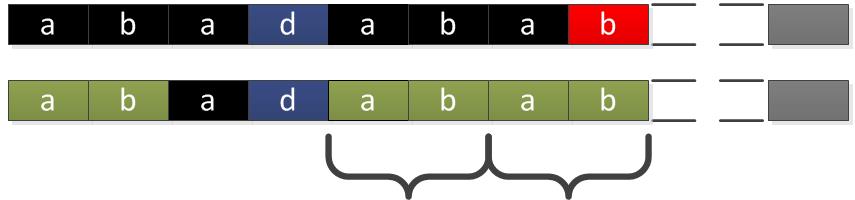
        对于两个相同的字符串，如图：

             

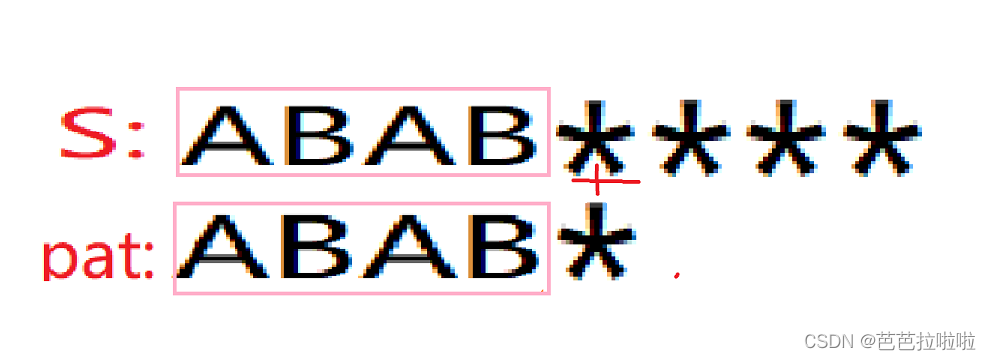
        我们已经知道它们的后一位匹配不成功，pat模式串需要往后移进行下一次的匹配。那么我们应该怎样确定后移的位数？

    

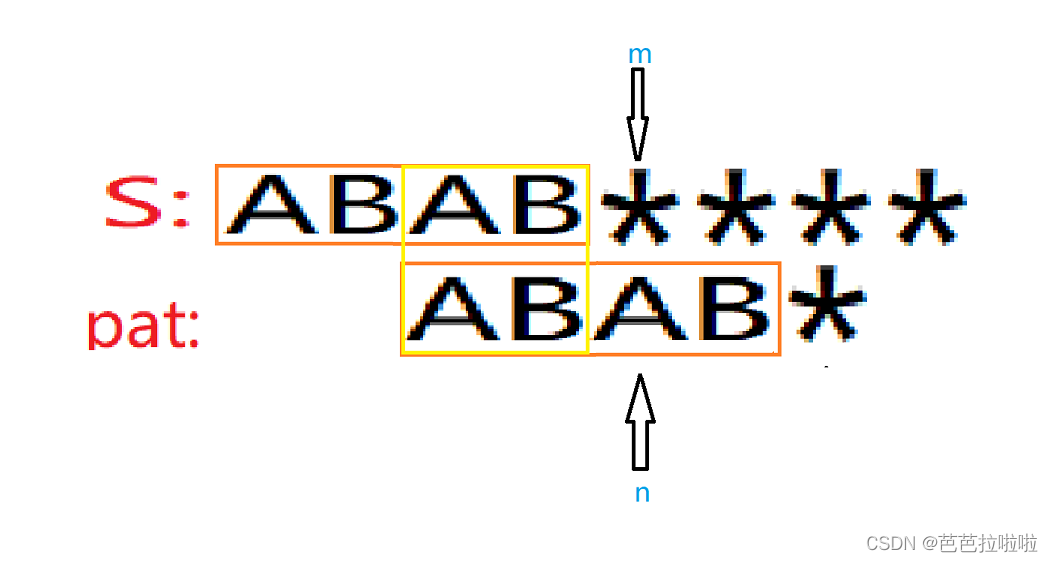
        根据后移的结果我们不难发现，黄框所框住的部分是相同的。这是因为我们在找到匹配的位置后，在pat模式串中，n指针前面的字符肯定与S后面的字符相同。

         在回到之前匹配失败的场景，我们在后移pat模式串时，只要满足匹配后S中已匹配的字符串中后面的一部分与pat串前面的一部分相同，由于我们已经确定了S与pat前 (n-1)个字符相同，而pat串又是确定的，可以直接用pat的前(n-1)个字符进行讨论。

                  

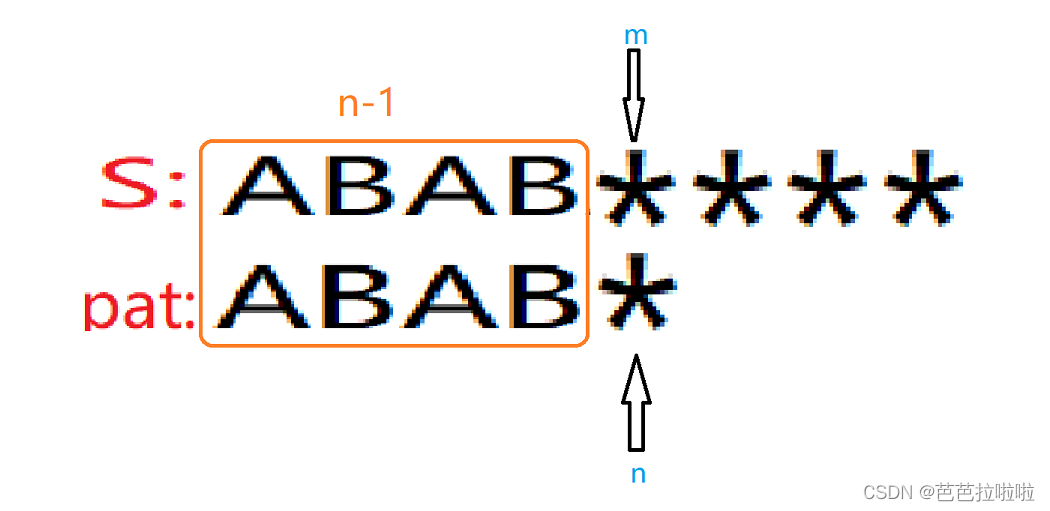
        对字符串ABAB，将除了最后一个字符，包含第一个的所有连续组合称为前缀；

如：A，AB，ABA 

        后缀也同理，如：B，AB，BAB

可以发现，它的最长公共前后缀为 AB，也就是说，我们在下次匹配的时候可以直接在第三个位置进行匹配。

如图：

        

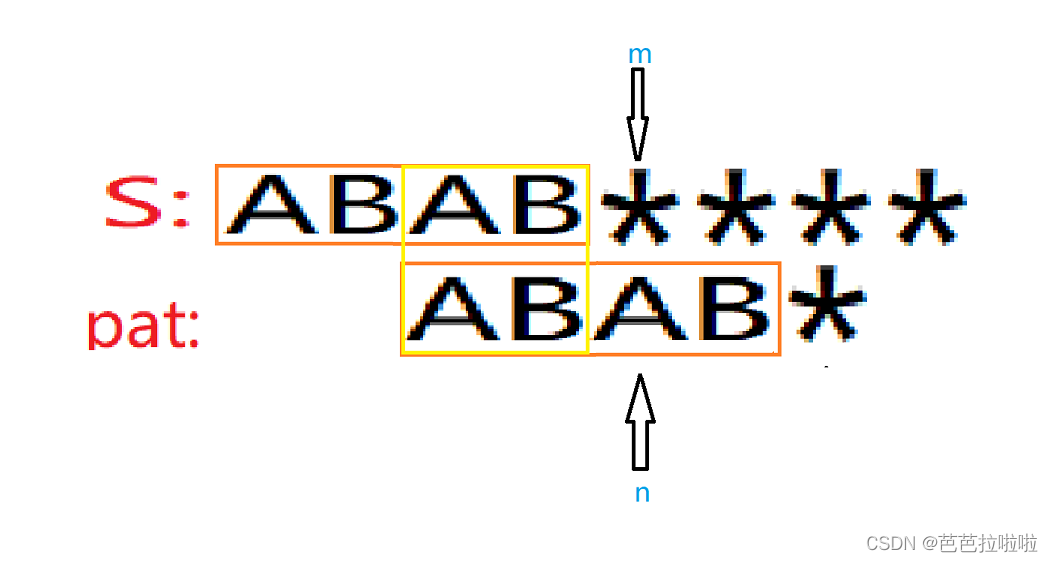
由于每次匹配成功的位数不相同，我们可以制订一个表格来表示它的最长公共前后缀长度。

模式串	A	B	A	B	D
最长公共前后缀长度	0	0	1	2	0

这样我们就能在匹配失败时知道n应该去的位置。但是某一位匹配失败要查它前一位的最长公共前后缀长度，而模式串的最后一位的最长公共前后缀长度没有用处，而如果pat模式串第一位与m指针指向的字符不匹配时又无法使m指针后移，不如直接设定一个next数组来表示：

模式串	A	B	A	B	D
next[]	-1	0	0	1	2

当next数组值为-1时，m指针后移一位。

由于next数组需要先通过pat字符串进行求出，所以我们可以这样设计代码：

public class matching {int next[] = null;private void setNext(String pat){//在这里对next数组进行实现。}public int strStr(String s,String pat){setNext(pat);//下面就是该算法的实现。int n = 0;for (int m = 0 ; m < s.length() ; m++){if(n == -1 || s.charAt(m) == pat.charAt(n)){n++;}else{m--;n = next[n];}if(n == pat.length()){return m-n+1;}}return -1;}
}

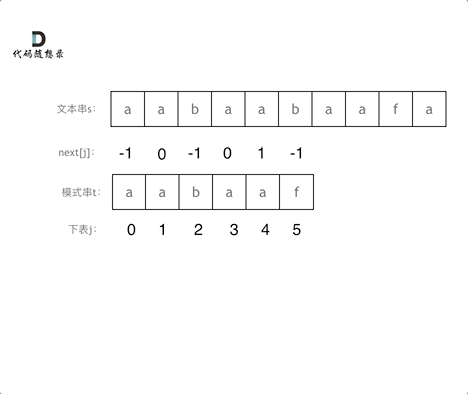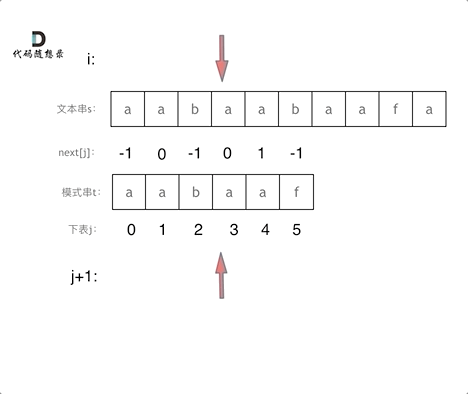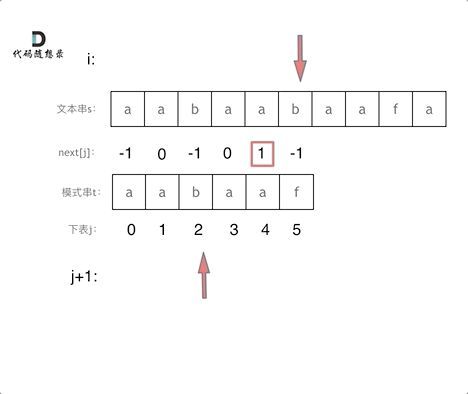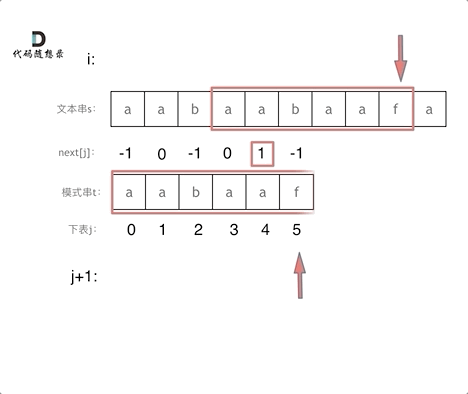
接下来讲讲next数组实现的算法：

next数组是由最长公共前后缀表演化而来，要想知道next数组，知道最长公共前后缀表就可以。

其实现算法如下：

    private void setNext(String pat){int[] next = new int[pat.length()];int[] tlc = new int[pat.length()];//tlc数组表示最长公共前后缀表for(int i = 1 , j = 0; i < pat.length() ; i++){while(j>0 && pat.charAt(i) != pat.charAt(j)){j = tlc[j-1];}//与KMP算法类似，找最长公共前后缀，再向后匹配。if(pat.charAt(i) == pat.charAt(j)){j++;}tlc[i] = j;}next[0] = -1;for(int x = 1 ; x < pat.length() ; x++){next[x] = tlc[x-1];}}

还有更为简单的实现方式，是直接实现next数组：

    private void GetNext(String pat){int j,k;j=0;k=-1;next[0]=-1;while (j<pat.length()-1) {if (k == -1 || pat.charAt(j) == pat.charAt(k)) {j++;k++;next[j] = k;} else {k = next[k];}}}

KMP算法的改进
为什么KMP算法这么强大了还需要改进呢？
我们来看一个例子:
字符串S = "aaaaabaaaaac"
模式串pat = "aaaaac"
这个例子中当‘b’与‘c’不匹配时应该‘b’与’c’前一位的‘a’比,这显然是不匹配的。'c’前的’a’回溯后的字符依然是‘a’。
我们知道没有必要再将‘b’与‘a’比对了，因为回溯后的字符和原字符是相同的，原字符不匹配，回溯后的字符自然不可能匹配。但是KMP算法中依然会将‘b’与回溯到的‘a’进行比对。这就是我们可以改进的地方了。我们改进后的next数组命名为：nextval数组。KMP算法的改进可以简述为： 如果a位字符与它next值指向的b位字符相等，则该a位的nextval就指向b位的nextval值，如果不等，则该a位的nextval值就是它自己a位的next值。 这应该是最浅显的解释了。

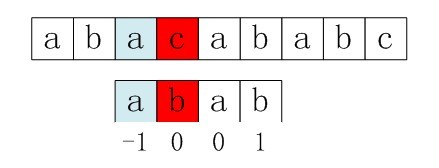
如字符串"ababaaab"的next数组以及nextval数组分别为：

下标	0	1	2	3	4	5	6	7
子串	a	b	a	b	a	a	a	b
next	-1	0	0	1	2	3	1	1
nextval	-1	0	-1	0	-1	3	1	0

下面是实现nextval数组的代码：

    private void GetNextVal(String pat){int j=0,k=-1;nextval[0]=-1;while (j<pat.length()){if (k==-1 || pat.charAt(j)==pat.charAt(k)){j++;k++;if (pat.charAt(j)!=pat.charAt(k))nextval[j]=k;elsenextval[j]=nextval[k];}else  k=nextval[k];}}

至此KMP算法就讲完了。

        但我在网上查有关KMP资料的时候，找到了另一种KMP算法的实现方式，这种实现方式相对来说更为复杂，同时效率在有些情况更高。

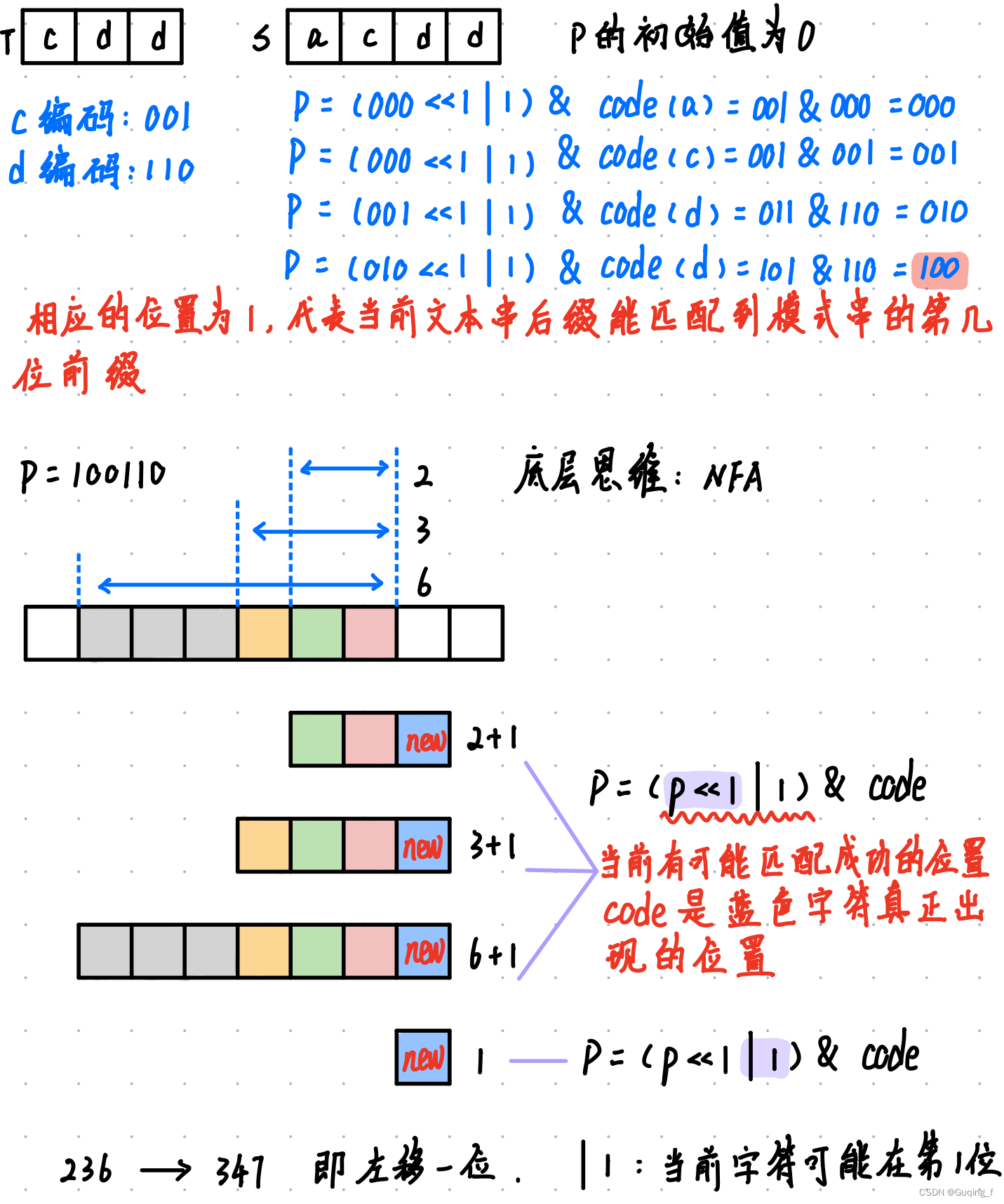
        这里引入一个概念：DFA，即有限状态自动机。

        不要听着觉得它很高大上，其实原理特别简单，通俗来讲就是如果一个东西，它遇见了下一个东西，会变成下一个状态。我们来看下面这个图：

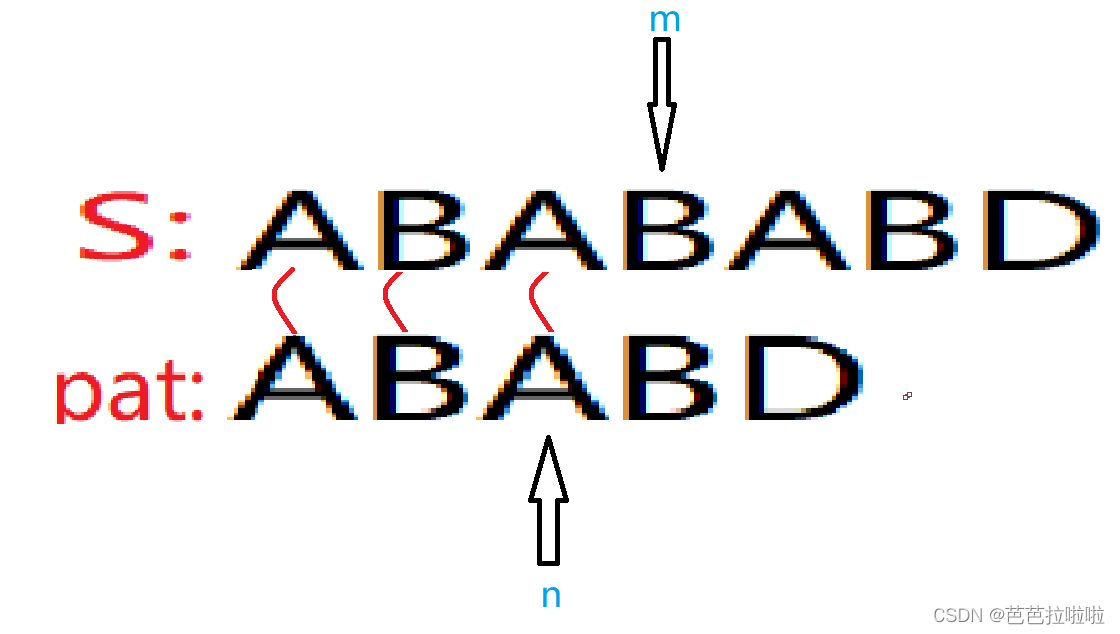
现在pat模式串处于 n 状态，当下次遇到 'B' 字符的时候，n指针可以向后移一位，pat模式串会到达 (n+1) 状态。

但如果是下面这种情况呢？

        

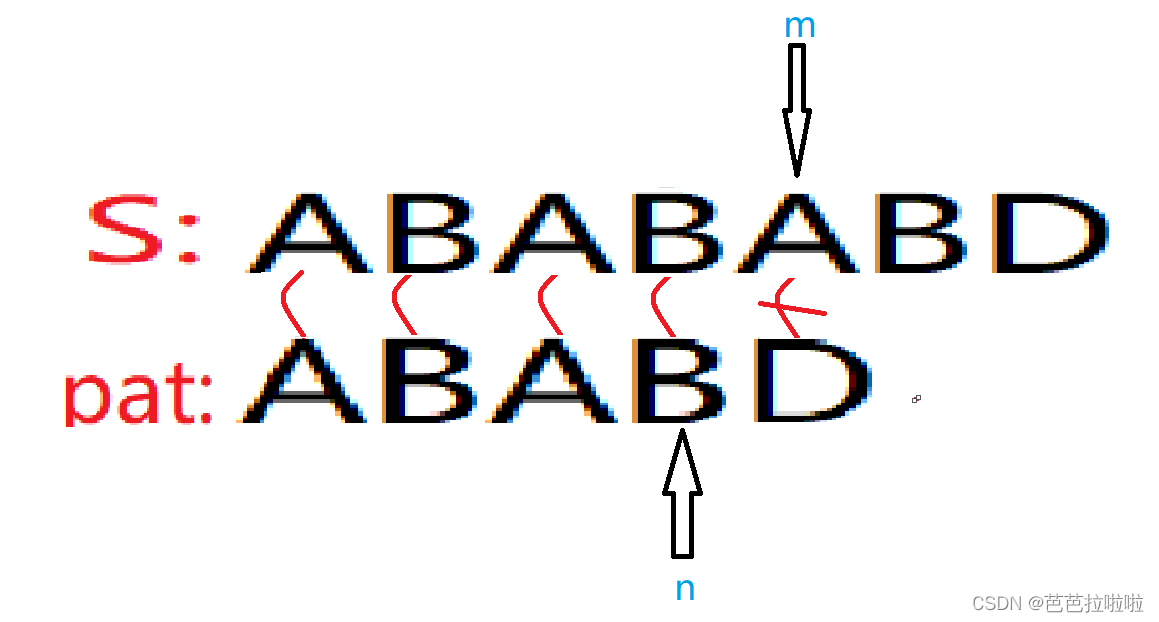
当pat串处于n状态时，此时遇到'A'字符，是不匹配的，然后pat应该到哪个状态。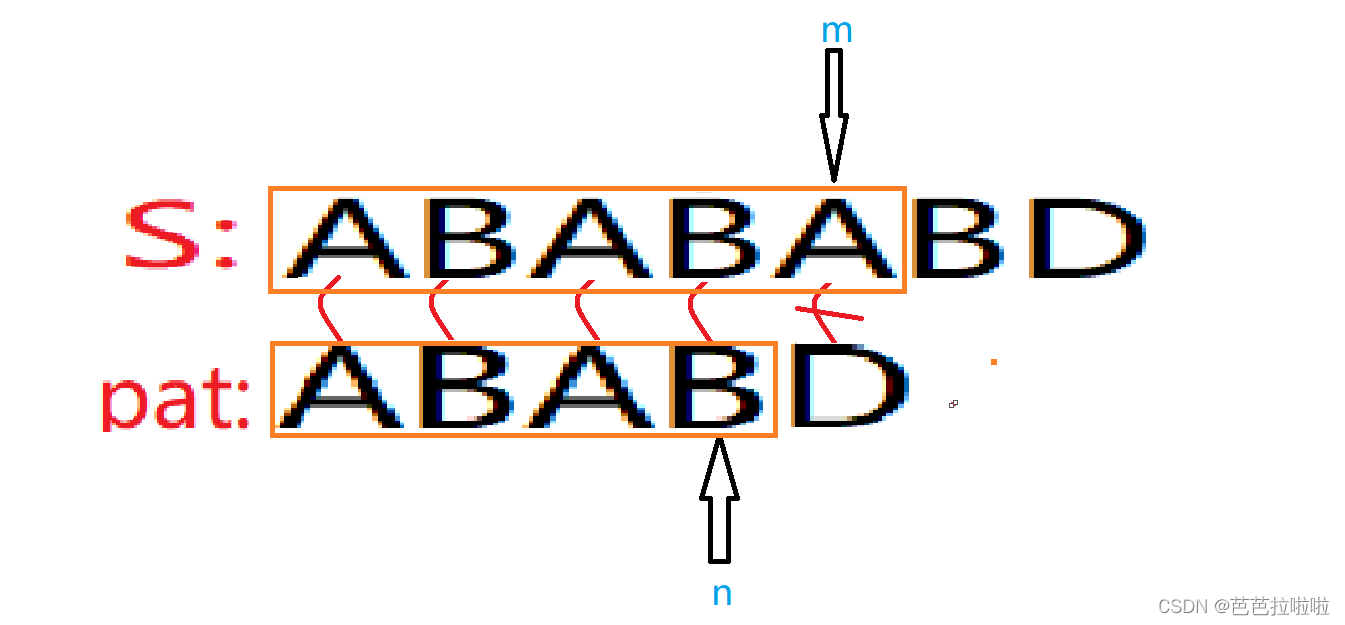

根据状态n和字符'A'，便可以确定一个新的字符串，pat串的前n个字符为它的最长前缀，只需找到新字符串的最长公共前后缀便可

以确定pat串下次该匹配的位置。如图：

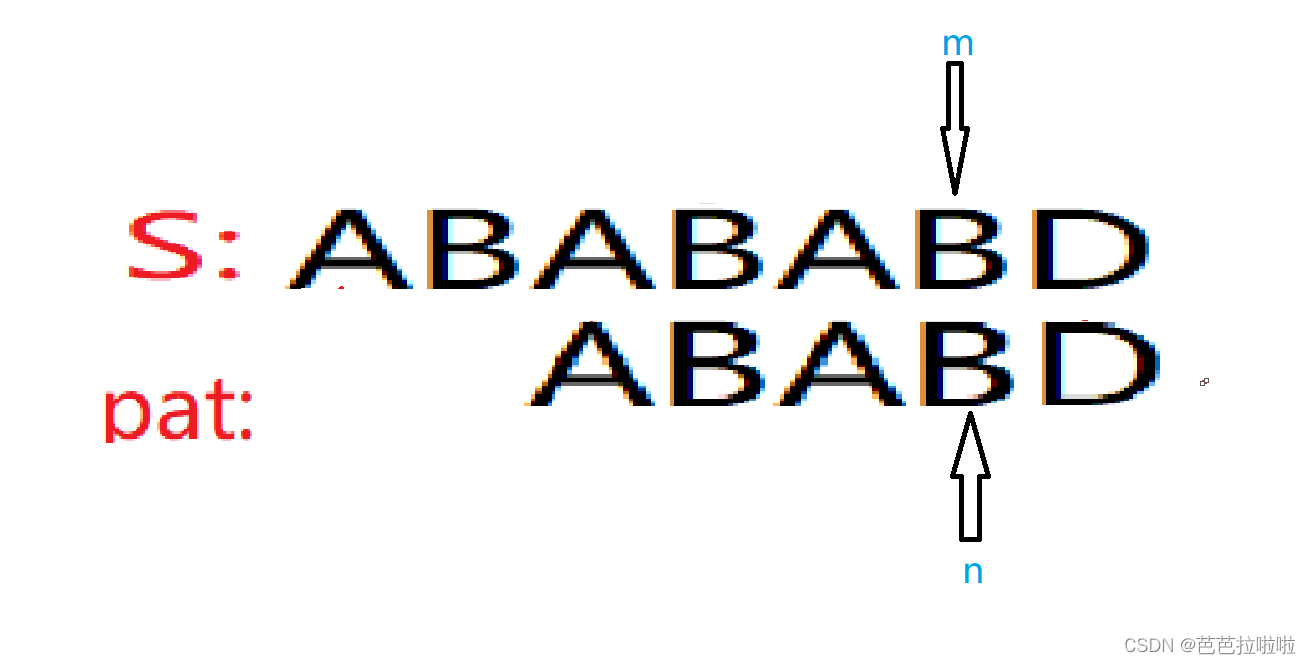
 这种方式有什么优点呢？

        我们可以发现，当m指针匹配不成功时，它会直接向右移动一位进行匹配而不是等待下次匹配。这就是比上个算法优化的地方。

        我们可以画个简易的状态关系图：

pat	A	B	A	B	D
A	1	1	3	1	3
B	0	2	0	4	0
C	0	0	0	0	0
D	0	0	0	0	5
E	0	0	0	0	0

        这个图就是有限状态自动机，它可以根据pat模式串匹配到的位置和下次遇到的字符来确定下次pat模式串得状态（即n指针的位置），从而实现“自动”。

基于数组快速的查找速度，我们可以将所有用到的字符都写入这个二维数组里，一般情况我们实现前256个字符：

代码如下：

    public void dfa(String pat) {this.pat = pat;int M = pat.length();dfa = new int[M][256];dfa[0][pat.charAt(0)] = 1;int X = 0;for (int j = 1; j < M; j++) {for (int c = 0; c < 256; c++) {if (pat.charAt(j) == c)dfa[j][c] = j + 1;elsedfa[j][c] = dfa[X][c];}X = dfa[X][pat.charAt(j)];}}

其实现原理与next数组构造有异曲同工之处，其他代码的实现也与上一种方法大致相同。