KMP算法

KMP算法是一种高效的字符串匹配算法，在传统暴力遍历匹配的基础上做了一定的优化。

首先KMP算法的实现也是使用了回退思想，不过与暴力遍历不同，KMP的回退，是让子串进行匹配，而不是主串。

KMP示例

首先我们来看两个例子来理解KMP算法：

例1：

分别从str的i和sub的j位置处开始匹配：

此时a与c不匹配，如果暴力遍历的话，是i回到到b，j也回到a，重新一轮匹配。而KMP算法，是将子串的j回到第二个a，str[i]与sub[j]重新开始匹配。原因很明显，第二个ab与第一个ab是相同的，因为这一部分主串与子串是匹配的，所以在主串中也是这样，因而主串的后半部分的ab就匹配了子串的前半部分ab，就省去了再重新匹配的过程，直接继续之前的部分匹配结果再向后匹配。

继续匹配：

再看一个例2：

开始匹配：

我们看到，此时a 与 c不匹配，如果暴力遍历的话，是i回到到b，j也回到a，重新一轮匹配。而KMP算法，是将子串的j回到a，str[i]与sub[j]重新开始匹配。

很多人可能疑问，为什么是这样？好像很有道理的样子

我们仔细观察，在子串中，j所指的c之前，除了最开头的a，找不到已经与主串匹配好了的字符串ab或者是a(要与c相邻)，**注意，是除了最开头的a。**正是因为在这段区间找不到ab或a，所以才从头再开始遍历。i不动，因为在i前面的主串中已经找不到与abc(子串的前三个字符)匹配的字符串了。

j回到最开始后，再开始匹配：

与之前一样，在j所指的d之前，除了最开头的a，找不到与主串已经匹配好了的abc或ab或a，所以j又要重新回头，到最开始。

再次遍历：

KMP核心

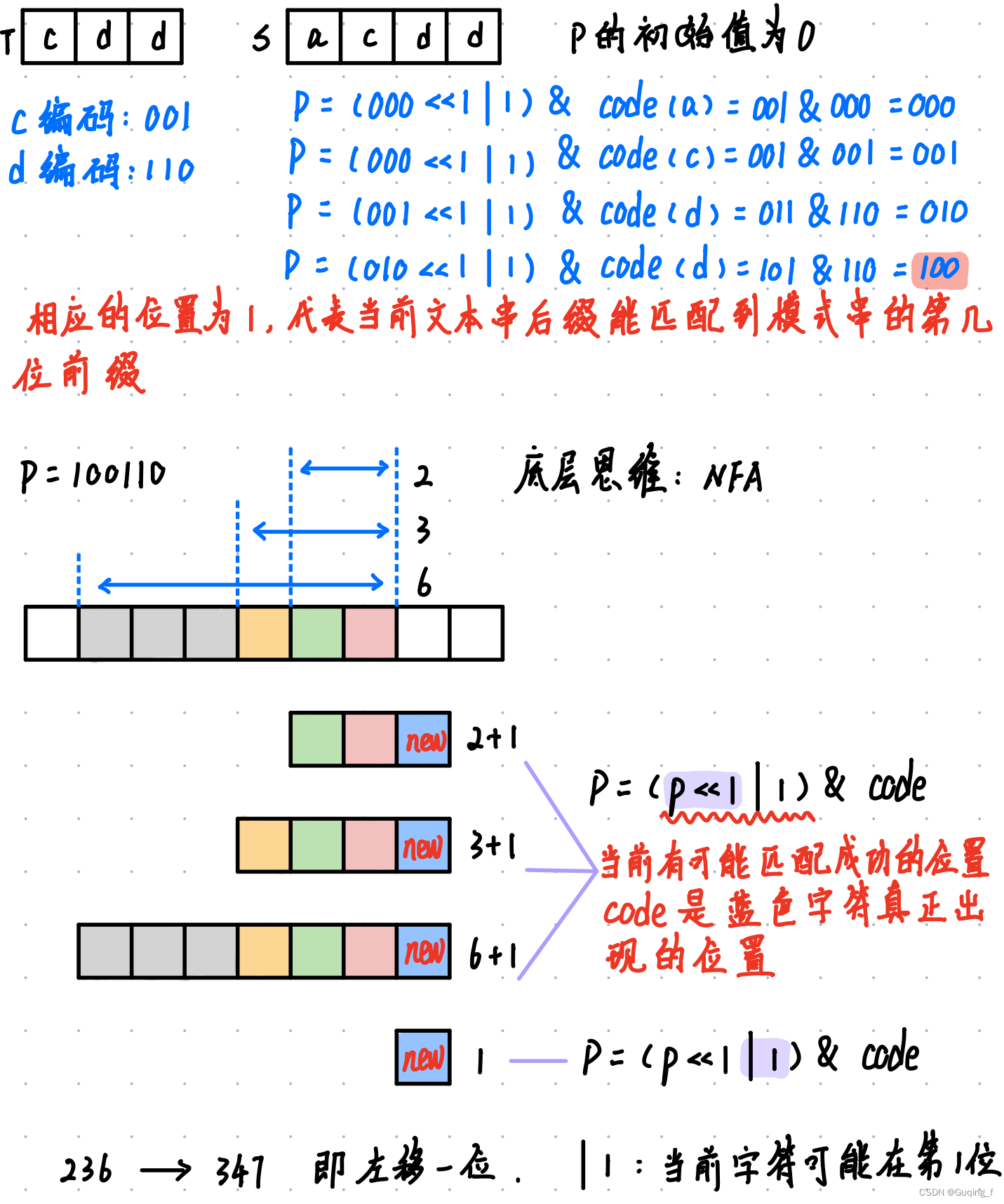
看完上述过程后，我们要实现这种让子串回头的方法，就是定义一个next数组，里面对应子串中每一个字符出现不匹配情况时，要回头到达的位置。

KMP 的精髓就是 next 数组：也就是用 next[j] = k;来表示，每个j 都对应一个 K 值， 这个 K 就是将来j要移动时，要移动到的位置。
而 K 的值是这样求的：
1、规则：找到匹配成功部分的两个相等的真子串(不包含本身)，一个以下标 0 字符开始，另一个以 j-1 下标字符结尾。
2、不管什么数据，next[0] = -1;next[1] = 0;
3、如果找得到，则k值等于相等的子串的长度；如果找不到，则k值等于0，即回到a

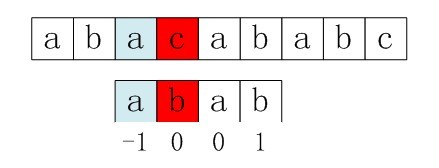
以例1中的子串为例：ababc

我们默认第一个和第二个字符出现不匹配情况时，next数组中存的值分别是-1和0。即，a不匹配时，k == -1，则需要主串的i向后走一步(这里先解释，可以到代码实现的时候再理解)，b不匹配时，回到a重新匹配。

第三个字符a如果出现不匹配情况，我们找已经匹配的相等的两个子串：以a开头的字符串，与以b结尾的字符串，很明显找不到，所以它要回到a，k = 0

第四个字符b出现不匹配情况时，同样找已经匹配的相等的两个子串：以a开头的字符串，以a结尾的字符串，可以找到字符串a，所以k = 1，即回到b

第四个字符c出现不匹配情况时，找已经匹配的相等的两个子串：以a开头的字符串，以a结尾的字符串，可以找到ab，所以k = 2，即回到第二个a

至此，子串的next数组就为：[-1, 0, 0, 1, 2]

两道求next数组的练习：

练习 1： ”ababcabcdabcde”

next数组：-1 0 0 1 2 0 1 2 0 0 1 2 0 0

练习 2： ”abcabcabcabcdabcde”

next数组：-1 0 0 0 1 2 3 4 5 6 7 8 9 0 1 2 3 0

建议大家自主完成，这有助于我们后面的理解

next数组求解

那么，如何用代码求出next数组呢？

求sub[j]的k值

1、当sub[j-1] == sub[k]时(k为sub[j-1]的k值)

同样以ababc为例

我们已知前面四个字符的next数组为:[-1, 0, 0, 1 ]，求c的k值

如果按照上面的求法，我们知道k = 2，但仔细观察，c前面的b，即sub[j - 1]，与第二个字符b，即sub[k]相同(该k为前一个字符b的k值)，第二个b之前已经匹配的子串aba中，两个符合要求的相等的子串为a，而现在的匹配的子串为abab，这两个b相等，在前面字符k值的基础上，c的k值就可以简单地看成是前一个字符的k + 1，即c的k == 1+1 = 2

2、当sub[j-1] != sub[k]时

以ababcd为例

我们已知ababcd的前五个字符的next数组:[-1, 0, 0, 1, 2]，求d的k值

很明显，在已经匹配的子串ab中，找不到相等的两个子串：以a开头的字符串，以c结尾的字符串。所以d要回退到最开始的a处。

此时的j指向d，且sub[j - 1] != sub[k]，即c != a，d应该回退到元素sub[k] (即第二个a)的k值处，也就是d的k == next[k] = 0

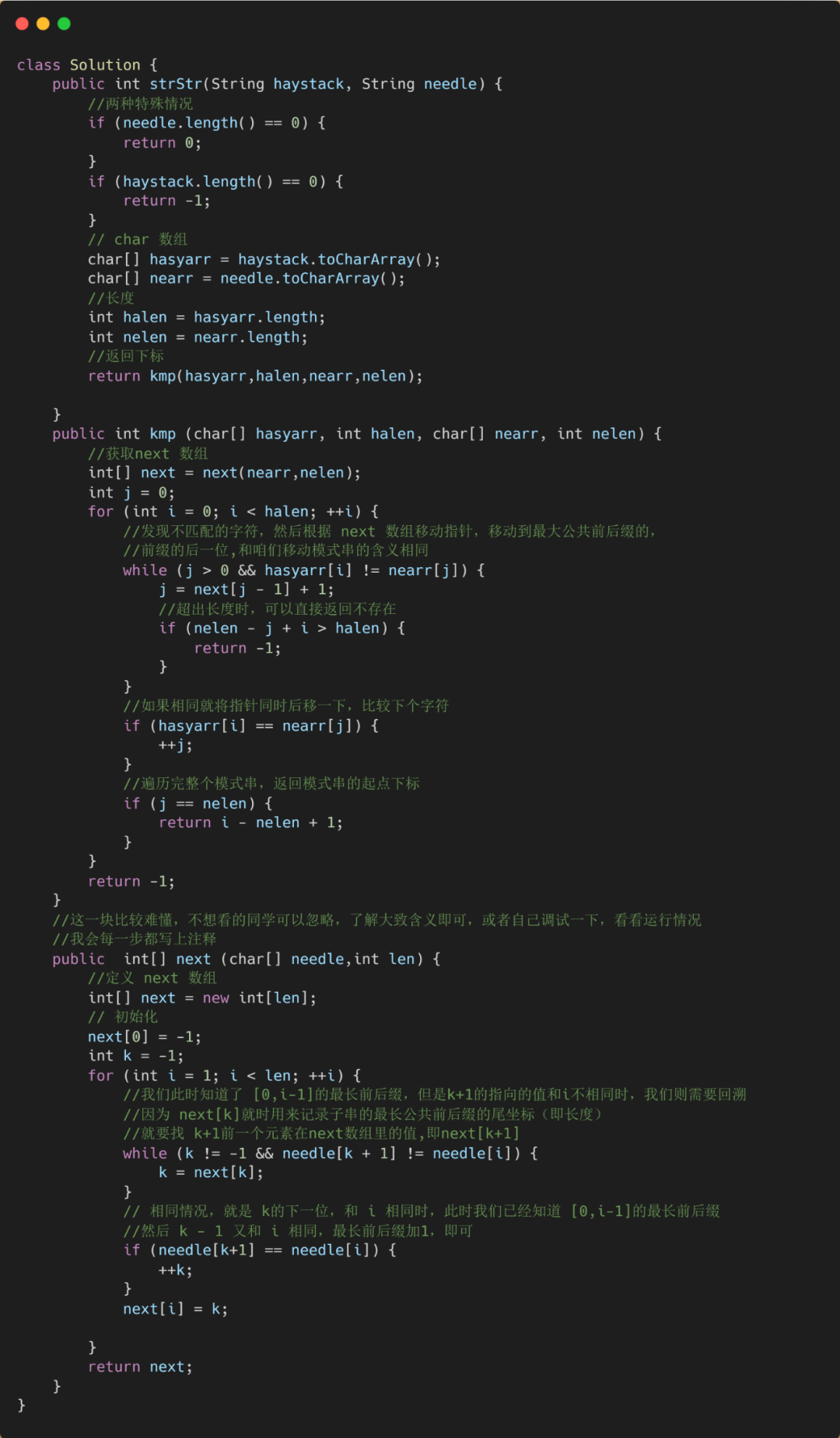
代码实现：

1、求出next数组

分两种情况：

1. sub[j-1] == sub[k]
2. sub[j-1] != sub[k]
   还有一种情况之前我们没有提到，就是回退到了最开始元素的k值处，即-1.此时说明主串中的字符与j及j之前的所有字符串都不匹配，所以需要向后走一步，从下一个字符再重新开始匹配

void GetNext(vector<int>& next, const string& subStr, int n)
{//默认处理next[0] = -1;next[1] = 0;int i = 2;//从第3个元素开始处理int k = 0;//表示i的前一个元素的next数组元素值while (i < n){//可能回退至首元素了,说明当前元素需要重新匹配，即从首元素开始，所以也是k = k + 1if (k == -1 || subStr[i - 1] == subStr[k])//P[i - 1] == P[k]{k = k + 1;next[i] = k;i++;}else//不匹配则回退{k = next[k];}}}

2、匹配逻辑的实现

与暴力求解类似，只不过当字符不相等时，不是双方都回头，而是子串回头。正因为子串会回退，当回退的下标j == -1时，表明主串需要向后走。

完整代码：

#include<iostream>
#include<string>
#include<vector>using namespace std;void GetNext(vector<int>& next, const string& subStr, int n)
{next[0] = -1;next[1] = 0;int i = 2;int k = 0;//表示i的前一个元素的next数组元素值while (i < n){//可能回退至首元素了,说明主串需要向后走，子串从首元素开始，所以也是k = k + 1if (k == -1 || subStr[i - 1] == subStr[k])//P[i - 1] == P[k]{k = k + 1;next[i] = k;i++;}else//不匹配则回退{k = next[k];}}}int KMP(const string& str, const string& subStr, int pos)//从主串的str位置开始匹配
{int strLength = str.size();int subLength = subStr.size();if (str.empty() || subStr.empty()) { return -1; }if (pos >= strLength || pos < 0) { return -1; }vector<int> next(subLength);//子串的next数组GetNext(next, subStr, subLength);int stri = pos;//遍历strint subj = 0;//遍历subStrwhile (stri < strLength && subj < subLength){//回退至子串第一个元素还未匹配，或者正常匹配，都需要将两个坐标+1if (subj == -1 || str[stri] == subStr[subj]){stri++;subj++;}else//不匹配了，回退{subj = next[subj];}}if (subj == subLength)//说明匹配到位了{//返回主串的起始匹配位置return stri - subLength + 1;}return -1;
}

next数组的优化

以子串aaaaaaaab为例，它的next数组为:[-1, 0, 1, 2, 3, 4, 5, 6, 7]当主串字符str[i] != 子串中的最后一个a时，匹配的字符回退到下标6的字符a，此时str[i]还是 != a，所以依旧需要回退，一直回退到第一个字符a

对于这种情况，我们可以做一个优化，当回退的字符s2与当前字符s1相同，则继续回退至s2的k值处，一直回退到不相等或者最开始处。所以s1的k值就等于s2的k值。

练习：模式串 t=‘abcaabbcabcaabdab’ ，该模式串的 next 数组的值为（ D ） ， nextval 数组的值为 （F）。
A． 0 1 1 1 2 2 1 1 1 2 3 4 5 6 7 1 2 B． 0 1 1 1 2 1 2 1 1 2 3 4 5 6 1 1 2
C． 0 1 1 1 0 0 1 3 1 0 1 1 0 0 7 0 1 D． 0 1 1 1 2 2 3 1 1 2 3 4 5 6 7 1 2
E． 0 1 1 0 0 1 1 1 0 1 1 0 0 1 7 0 1 F． 0 1 1 0 2 1 3 1 0 1 1 0 2 1 7 0 1

注意：这里是将第一个元素和第二个元素的初始k值设置为0和1，所以我们只要把求出的结果+1即可