1、引言

地理坐标：为球面坐标。参考平面地是椭球面,坐标单位:经纬度

大地坐标：为平面坐标。参考平面地是水平面,坐标单位：米、千米等

地理坐标转换到大地坐标的过程可理解为投影。（投影：将不规则的地球曲面转换为平面）

在ArcGIS中预定义了两套坐标系：地理坐标系（Geographic coordinate system）投影坐标系（Projected coordinate system）

1.1 首先理解地理坐标系（Geographic coordinate system）

Geographic coordinate system直译为地理坐标系统，是以经纬度为地图的存储单位的。很明显，Geographic coordinate syst em是球面坐标系统。我们要将地球上的数字化信息存放到球面坐标系统上，如何进行操作呢？地球是一个不规则的椭球，如何将数据信息以科学的方法存放到椭球上？这必然要求我们找到这样的一个椭球体。这样的椭球体具有特点：可以量化计算的。具有长半轴，短半轴，偏心率。以下几行便是Krasovsky_1940椭球及其相应参数。

Spheroid: Krasovsky_1940

Semimajor Axis: 6378245.000000000000000000

Semiminor Axis: 6356863.018773047300000000

Inverse Flattening（扁率）: 298.300000000000010000

然而有了这个椭球体以后还不够，还需要一个大地基准面将这个椭球定位。在坐标系统描述中，可以看到有这么一行：

Datum: D_Beijing_1954 表示，大地基准面是D_Beijing_1954。

--------------------------------------------------------------------------------
有了Spheroid和Datum两个基本条件，地理坐标系统便可以使用。
完整参数：

Alias:
Abbreviation:
Remarks:
Angular Unit: Degree (0.017453292519943299)
Prime Meridian（起始经度）: Greenwich (0.000000000000000000)
Datum（大地基准面）: D_Beijing_1954
Spheroid（参考椭球体）: Krasovsky_1940
Semimajor Axis: 6378245.000000000000000000
Semiminor Axis: 6356863.018773047300000000
Inverse Flattening: 298.300000000000010000

1.2 接下来便是Projection coordinate system（投影坐标系统），首先看看投影坐标系统中的一些参数。

Projection: Gauss_Kruger
Parameters:
False_Easting: 500000.000000
False_Northing: 0.000000
Central_Meridian: 117.000000
Scale_Factor: 1.000000
Latitude_Of_Origin: 0.000000
Linear Unit: Meter (1.000000)
Geographic Coordinate System:
Name: GCS_Beijing_1954

Alias:
Abbreviation:
Remarks:
Angular Unit: Degree (0.017453292519943299)
Prime Meridian: Greenwich (0.000000000000000000)
Datum: D_Beijing_1954
Spheroid: Krasovsky_1940
Semimajor Axis: 6378245.000000000000000000
Semiminor Axis: 6356863.018773047300000000
Inverse Flattening: 298.300000000000010000

从参数中可以看出，每一个投影坐标系统都必定会有Geographic Coordinate System。

投影坐标系统，实质上便是平面坐标系统，其地图单位通常为米。

那么为什么投影坐标系统中要存在坐标系统的参数呢？

这时候，又要说明一下投影的意义：将球面坐标转化为平面坐标的过程便称为投影。

好了，投影的条件就出来了：

a、球面坐标

b、转化过程（也就是算法）

也就是说，要得到投影坐标就必须得有一个“拿来”投影的球面坐标，然后才能使用算法去投影！

即每一个投影坐标系统都必须要求有Geographic Coordinate System参数。

关于北京54和西安80是我们使用最多的坐标系
先简单介绍高斯-克吕格投影的基本知识，了解就直接跳过，我国大中比例尺地图均采用高斯-克吕格投影，其通常是按6度和3度分带投影，1:2.5万－1:50万比例尺地形图采用经差6度分带，1:1万比例尺的地形图采用经差3度分带。具体分带法是：6度分带从本初子午线开始，按经差6度为一个投影带自西向东划分，全球共分60个投影带，带号分别为1－60；3度投影带是从东经1度30秒经线开始，按经差3度为一个投影带自西向东划分，全球共分120个投影带。

为了便于地形图的测量作业，在高斯-克吕格投影带内布置了平面直角坐标系统，具体方法是，规定中央经线为X轴，赤道为Y轴，中央经线与赤道交点为坐标原点，x值在北半球为正，南半球为负，y值在中央经线以东为正，中央经线以西为负。由于我国疆域均在北半球，x值均为正值，为了避免y值出现负值，规定各投影带的坐标纵轴均西移500km，中央经线上原横坐标值由0变为500km。为了方便带间点位的区分，可以在每个点位横坐标y值的百千米位数前加上所在带号，如20带内A点的坐标可以表示为YA=20 745921.8m。

    在Coordinate Systems\Projected Coordinate Systems\Gauss Kruger\Beijing 1954目录中，我们可以看到四种不同的命名方式：
    Beijing 1954 3 Degree GK CM 75E.prj
    Beijing 1954 3 Degree GK Zone 25.prj
    Beijing 1954 GK Zone 13.prj
    Beijing 1954 GK Zone 13N.prj

    对它们的说明分别如下：
    三度分带法的北京54坐标系，中央经线在东75度的分带坐标，横坐标前不加带号
    三度分带法的北京54坐标系，中央经线在东75度的分带坐标，横坐标前加带号
    六度分带法的北京54坐标系，分带号为13，横坐标前加带号
    六度分带法的北京54坐标系，分带号为13，横坐标前不加带号

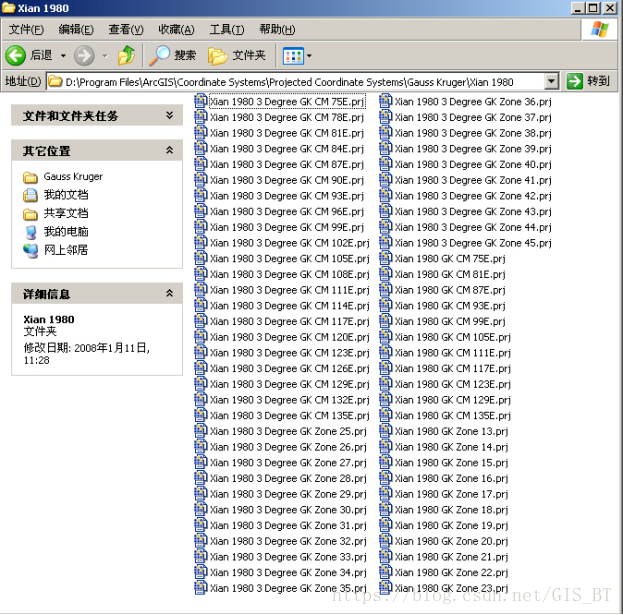
在Coordinate Systems\Projected Coordinate Systems\Gauss Kruger\Xian 1980目录中，文件命名方式又有所变化：
    Xian 1980 3 Degree GK CM 75E.prj
    Xian 1980 3 Degree GK Zone 25.prj
    Xian 1980 GK CM 75E.prj
    Xian 1980 GK Zone 13.prj

对它们的说明分别如下：
    三度分带法的西安80坐标系，中央经线在东75度的分带坐标，横坐标前不加带号
    三度分带法的西安80坐标系，中央经线在东75度的分带坐标，横坐标前加带号
    六度分带法的西安80坐标系，中央经线在东75度的分带坐标，横坐标前不加带号
    六度分带法的西安80坐标系，分带号为13，横坐标前加带号

西安80坐标文件的命名方式、含义和北京54前两个坐标相同，但没有出现“带号+N”这种形式，为什么没有采用统一的命名方式？让人看了有些费解。

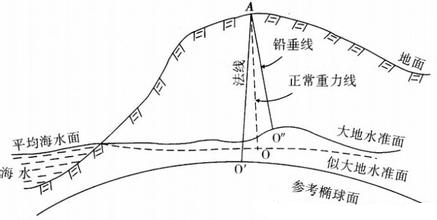
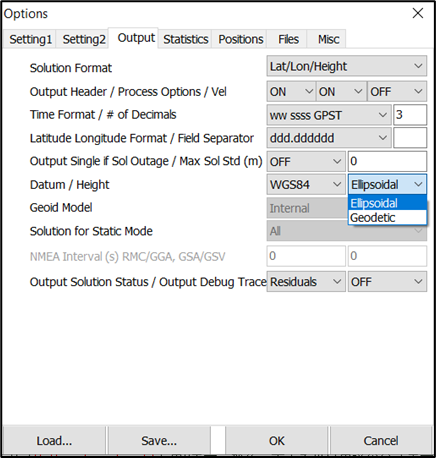
大地坐标（GeodeticCoordinate）:大地测量中以参考椭球面为基准面的坐标。地面点P的位置用大地经度L、大地纬度B和大地高H表示。当点在参考椭球面上时，仅用大地经度和大地纬度表示。大地经度是通过该点的大地子午面与起始大地子午面之间的夹角，大地纬度是通过该点的法线与赤道面的夹角，大地高是地面点沿法线到参考椭球面的距离。

方里网:是由平行于投影坐标轴的两组平行线所构成的方格网。因为是每隔整公里绘出坐标纵线和坐标横线，所以称之为方里网，由于方里线同时又是平行于直角坐标轴的坐标网线，故又称直角坐标网。

在1：1万——1：20万比例尺的地形图上，经纬线只以图廓线的形式直接表现出来，并在图角处注出相应度数。为了在用图时加密成网，在内外图廓间还绘有加密经纬网的加密分划短线(图式中称“分度带”)，必要时对应短线相连就可以构成加密的经纬线网。1：25万地形图上，除内图廓上绘有经纬网的加密分划外，图内还有加密用的十字线。

我国的1：50万——1：100万地形图，在图面上直接绘出经纬线网，内图廓上也有供加密经纬线网的加密分划短线。

直角坐标网的坐标系以中央经线投影后的直线为X轴，以赤道投影后的直线为Y轴，它们的交点为坐标原点。这样，坐标系中就出现了四个象限。纵坐标从赤道算起向北为正、向南为负；横坐标从中央经线算起，向东为正、向西为负。

虽然我们可以认为方里网是直角坐标，大地坐标就是球面坐标。但是我们在一副地形图上经常见到方里网和经纬度网，我们很习惯的称经纬度网为大地坐标，这个时候的大地坐标不是球面坐标，她与方里网的投影是一样的（一般为高斯投影），也是平面坐标。