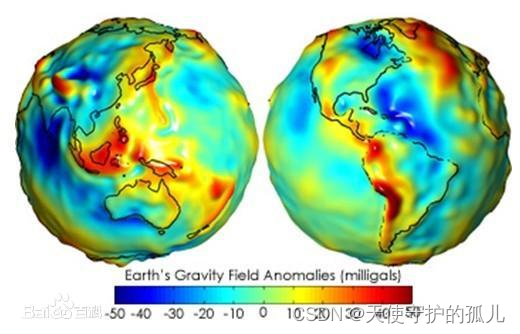
大地水准面

指平均海平面通过大陆延伸勾画出的一个连续的封闭曲面。大地水准面包围的球体称为大地球体。从大地水准面起算的陆地高度，称为绝对高度或海拔。

大地水准面是对地球的一次逼近！

地球椭球体

也称为拟地球椭球体、似地球椭球体，近似的代表地球大小和形状的数学曲面，一般采用旋转椭球。其大小和形状常用长半径a和扁率α表示。1980年中国国家大地坐标系采用国际大地测量学与地球物理学联合会第十六届大会推荐的1975年椭球参考值：a=6378140，α=1∶298257。

地球椭球体对地球的二次逼近！
在这里插入图片描述

参考椭球体

形状、大小一定，且经过定位，定向的地球椭球体称为参考椭球。是与某个区域如一个国家大地水准面最为密和的椭球面。

参考椭球面是测量计算的基准面，法线是测量计算的基准线。我国的大地原点，即椭球定位做最佳拟合的参考点位于陕西省泾阳县永乐镇。

大地基准面

用于尽可能与大地水准面密合的一个椭球曲面，是人为确定的。椭球面和地球肯定不是完全贴合的，因而，即使用同一个椭球面，不同的地区由于关心的位置不同，需要最大限度的贴合自己的那一部分，因而大地基准面就会不同。椭球体与大地基准面之间的关系是一对多的关系，也就是基准面是在椭球体基础上建立的，但椭球体不能代表基准面，同样的椭球体能定义不同的基准面，如前苏联的Pulkovo 1942、非洲索马里的Afgooye基准面都采用了Krassovsky椭球体，但它们的大地基准面显然是不同的。

每个国家或地区均有各自的基准面，我们通常称谓的北京54坐标系、西安80坐标系实际上指的是我国的两个大地基准面。我国参照前苏联从1953年起采用克拉索夫斯基(Krassovsky)椭球体建立了我国的北京54坐标系，1978年采用国际大地测量协会推荐的1975地球椭球体（IAG75）建立了我国新的大地坐标系–西安80坐标系，~~目前大地测量基本上仍以北京54坐标系作为参照~~ ，北京54与西安80坐标之间的转换可查阅国家测绘局公布的对照表。WGS1984基准面采用WGS84椭球体，它是一地心坐标系，即以地心作为椭球体中心，目前GPS测量数据多以WGS1984为基准。因此相对同一地理位置，不同的大地基准面，它们的经纬度坐标是有差异的。

在这里插入图片描述
地理（大地）坐标系

地球上任意一点通常用经度和纬度来决定。经线和纬线是地球表面上两组正交（相交为90度）的曲线，这两组正交的曲线构成的坐标，称为地理坐标系。

地图投影

将地球球面坐标转化为平面坐标的过程便是投影过程；投影所需要的必要条件是：

第一、任何一种投影都必须基于一个椭球（地球椭球体）；
第二、将球面坐标转换为平面坐标的过程（投影算法）。简单的说投影坐标系是地理坐标系+投影过程。

常用地图投影

高斯–克吕格投影（Gauss-Kruger），横轴等角切椭圆柱投影。又称横轴墨卡托投影（TM），我国基本比例尺地形图1：5000，1:1万，1:2.5万，1:5万，1：10万，1:25万，1:50万都采用该投影。
墨卡托投影(Ｍ，Mecator)：等角正切圆柱投影，航海图
通用墨卡托投影(UTM)：横轴等角割圆柱投影，改进的高斯投影
兰勃特投影(Lambert)：等角正轴割圆锥投影，1:100万和省图
阿尔伯斯投影(Albers)：正轴等面积割圆锥投影，省图

几个概念之间的关系

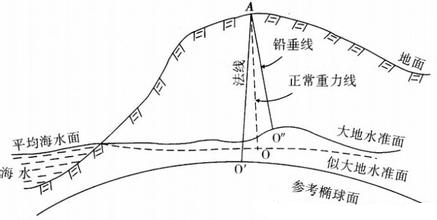
大地水准面，地球椭球体，大地基准面，地图投影几个概念的关系如下图所示：
在这里插入图片描述

那么现在让我们把地球椭球体和基准面结合起来看，在此我们把地球比做是“马铃薯”，表面凸凹不平，而地球椭球体就好比一个“鸭蛋”，那么按照我们前面的定义，基准面就定义了怎样拿这个“鸭蛋”去逼近“马铃薯”某一个区域的表面，X、Y、Z轴进行一定的偏移，并各自旋转一定的角度，大小不适当的时候就缩放一下“鸭蛋”，那么通过如上的处理必定可以达到很好的逼近地球某一区域的表面。

GIS的基本概念二：大地水准面、旋转椭球体（椭球体）、大地基准面
https://blog.csdn.net/kehongyong/article/details/16916825

请添加图片描述