学习地图学，由于地理知识欠缺，学习相关投影知识还为时过早，需要复习一些基本概念。

阅读对象:测绘类

地球自然球体: 由地球自然表面所包围的的形体称为地球自然体。

地球自然球体形状:地球不是一个正球体，而是一个极半径略短，赤半径略长，北极略突出，南极略扁平，近于梨形的椭球体

水准面：设想有一个自然平静的海水面，向陆地延伸而形成的封闭曲面，我们把自由平静的海水面成为水准面。

水准面是一个处处与重力方向垂直的连续曲面，是一个重力等位面（水准面有无数个）。

水平面：与水准面相切的平面。

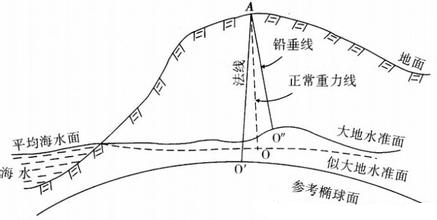
 （注意：该图的水准面过于平滑，实际水准面是凹凸不平，极不规则的，因为每一点的法线都与该点铅垂线重合，而地球质量分布不均匀，故每一点的重力方向都不尽相同）

大地水准面：水准面中最接近地球形状和大小的是通过平均海水面的那个水准面，这个唯一而确定的水准面叫做大地水准面。

大地水准面的形状：有微小起伏，近似于椭球体，其和一般水准面一样，任意一点的的法线都与该点的铅垂线重合。

大地体：大地水准面所包围的代表地球形状和大小的形体叫做大地体。（总体上看，大地体接近于一个具有微小偏率的旋转椭球）

旋转椭球体：以地球的南北短轴为旋转轴旋转而成的椭球形体，也称为地球椭球体，或简称为椭球体。

 

旋转椭球体的一些基本参数：长半径a，短半径b，偏率（a - b）/ a

第一偏心率：sqrt(a^2 b^2) / a     第二偏心率：sqrt(a^2 - b^2) / b

 

 

地轴：地球椭球旋转时所绕的短轴，它通过椭球中心O。他和地球旋转轴重合，又称地轴。

子午面：包含旋转轴的任一平面（有无数个）。

起始子午面：通过通过英国格林尼治天文台的子午面。（过本初子午线）

子午线：子午面与参考椭球面的交线，亦称经线。

纬线：垂直于旋转轴的任一平面与参考椭球面的交线。

赤道平面：过参考椭球面中心且垂直于旋转轴的平面

赤道：赤道平面与参考椭球面的交线。

极点：旋转轴与参考椭球面的交点，在北端的称为北极点，在南端的称为南极点。

 

？？？确定大地水准面和地球椭球面之间的相对关系（地球椭球的定位和定向）？？？

椭球定位是确定椭球中心的位置，分为两类：

局部定位：要求在一定范围内椭球面与大地水准面有最佳符合（后续会讲到），而对椭球的中心位置无特殊要求。

地心定位：要求在全球范围内椭球面与大地水准面有最佳的符合（后续会讲到），同时要求椭球中心（椭球的几何中心）与地球质心（地球的质量中心）一致或最为接近。

椭球定向是确定椭球旋转轴的方向，不论是局部定位还是地心定位，都应满足两个平行条件：

1. 椭球短轴平行于地球自转轴。

2. 大地起始子午面平行于天文起始子午面。

参考椭球：具有确定的参数（长半径a和偏率α或短半径b），经过局部定位和定向，在某一地区大地水准面最佳拟合的地球椭球，叫做参考椭球。（最佳拟合深入一点就是在地球表面适当位置选择一点p，令p的铅垂线 和 椭球面上相应的p。点的法线重合，并使p。点处椭球与大地水准面相切，这里的p点称为大地原点，旋转后的椭球面称为参考椭球面，其包围的形体，称为参考椭球体）

总地球椭球：除满足地心定位和双平行条件外，在确定的椭球参数时能使它在全球范围内与大地体最密合的地球椭球，叫做总地球椭球。

大地水准面和铅垂线是大地测量的基准面和基准线。

参考椭球面和法线是内业计算和制图的基准面和基准线。

大地原点选址：

1. 地质构造稳定。 2. 远离大城市，附近无大的工矿区。 3. 地形开阔，便于从事高精度测量。

4. 便于管理与保护。 5. 大致位于整个大地坐标覆盖地区的中部。

在大地测量学中，地理坐标分为三类：

1. 天文坐标系 2. 大地坐标系 3. 地心坐标系

1. 天文（地理）坐标系

天文地理坐标（又称天文坐标系）表示地面点在大地水准面上的位置。

基准：铅垂线和大地水准面。

描述：用天文经度和天文纬度，海拔高度（又叫正高）表示地面点在地球表面的位置

天文经度：观测点当地铅垂线所在南北方向平面（观测点的子午面）与本初子午面的夹角。

天文纬度：观测点的铅垂线与赤道面的夹角。

海拔高（正高）：观测点到 观测点在大地水准面的投影点的垂线距离。

2. 大地（地理）坐标系

 

大地地理坐标又称为大地坐标，是表示地面点在参考椭球面上的位置。

基准：参考椭球面和法线。

描述：用大地经度，大地纬度，大地高表示地面点在地球表面的位置。

大地经度：过p点的子午面NPS与起始子午面NMS所构成的二面角。

大地纬度：过p点的法线Pn与赤道平面的夹角。

大地高：空间点沿该点法线到椭球面的距离，向上为正，向下为负。

3.地心（地理）坐标系：

地心：地球椭球体的质量中心。

地心经纬度：（基准：以地球椭球体质量中心为基点）参考椭球上的任意一点和地心的连线与赤道平面的夹角为地心纬度。地心坐标系中本初子午面到某点的子午面的夹角（同大地纬度）。

参心坐标系：以参考椭球面为基本参考面，以大地原点为基本参考点，以参考椭球中心为基本参考中心的大地坐标系。

地心坐标系：以一个中心与地球质心重合，旋转椭球面与全球大地水准面有最佳密切吻合的地球椭球所建立的大地坐标系或以地球质心为原点建立的空间直角坐标。

三种坐标系中纬度的差异

其中ψ是地心纬度，φ是大地纬度，Φ天文维度。