本节介绍如何用Eigen求解线性最小二乘方程组。求解Ax=b的最小二乘问题，等价于求解方程

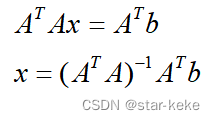
 使用Eigen的求解的代码如下：

    Eigen::MatrixXd MatX;//样本数据Eigen::MatrixXd MatY;//观测值Eigen::MatrixXd MatLS;//待定系数MatLS = (MatX.transpose() * MatX).inverse() * MatX.transpose() * MatY;

 直线拟合：

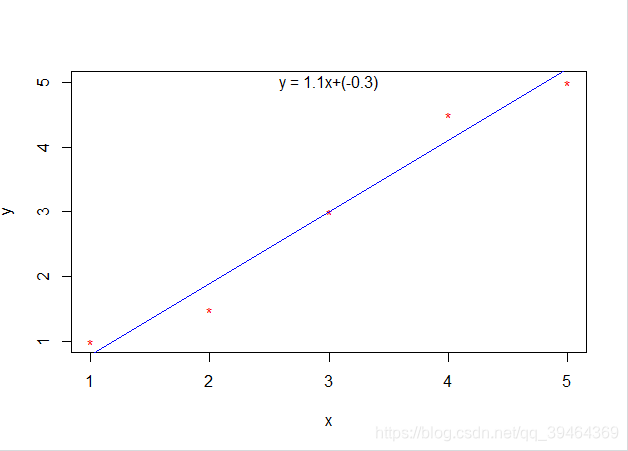
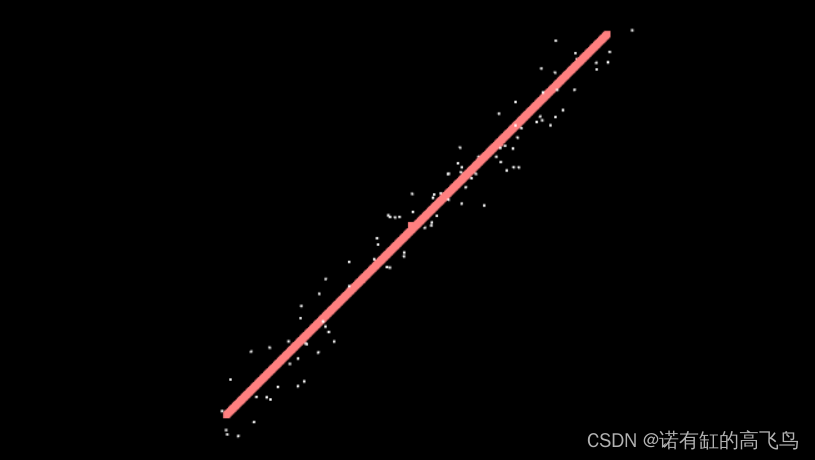
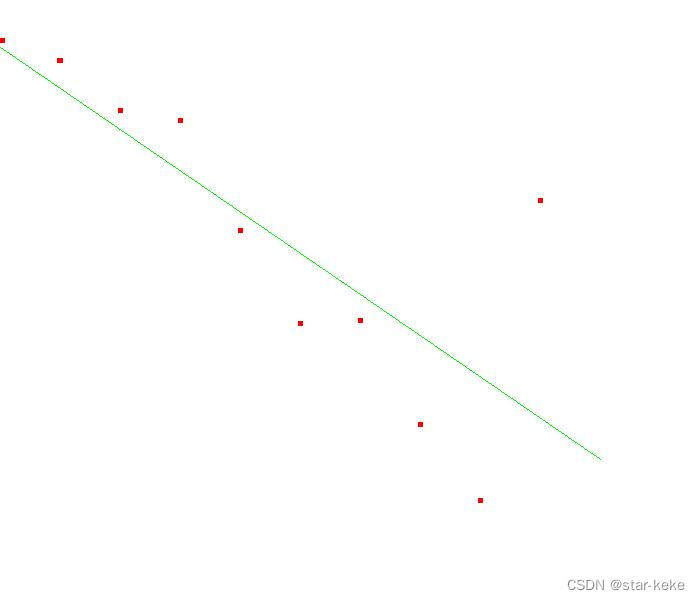
直线方程：y = k*x + b

//y = k*x + b
void least_square_line(double input[][2], int number, double&k, double&b){Eigen::MatrixXd MatX;Eigen::MatrixXd MatY;MatX.resize(number, 2);MatY.resize(number, 1);Eigen::MatrixXd MatLS;MatLS.resize(number, 1);for(int i = 0; i < number; ++i){MatX.row(i) = Eigen::Vector2d(input[i][0], 1);MatY(i, 0) = input[i][1];}MatLS = (MatX.transpose()*MatX).inverse()*MatX.transpose()*MatY;//MatLS = MatX.colPivHouseholderQr().solve(MatY); //也可以用k = MatLS(0,0);b = MatLS(1,0);
}

曲线拟合：

 多项式方程：Pn(x)=a(n)x^n+a(n-1)x^(n-1)+…+a(1)x+a(0)

//y = a0 + a1*x + a2*x*x + a3*x*x*x + a4*x*x*x*x + a5*x*x*x*x*x;
void least_square_curve(double input[][2], int number, int jie, std::vector<double>&weight){Eigen::MatrixXd MatX;Eigen::MatrixXd MatY;MatX.resize(number, jie);MatY.resize(number, 1);Eigen::MatrixXd MatLS;MatLS.resize(number, 1);for(int i = 0; i < number; ++i){std::vector<double> pows;for(int j = 0; j < jie; j++){double p =  pow(input[i][0], j);MatX(i, j) = p;}MatY.row(i)[0] = input[i][1];}MatLS = (MatX.transpose()*MatX).inverse()*MatX.transpose()*MatY;for(int i = 0; i < jie; i++)weight.push_back(MatLS(i, 0)) ;
}

3阶多项式

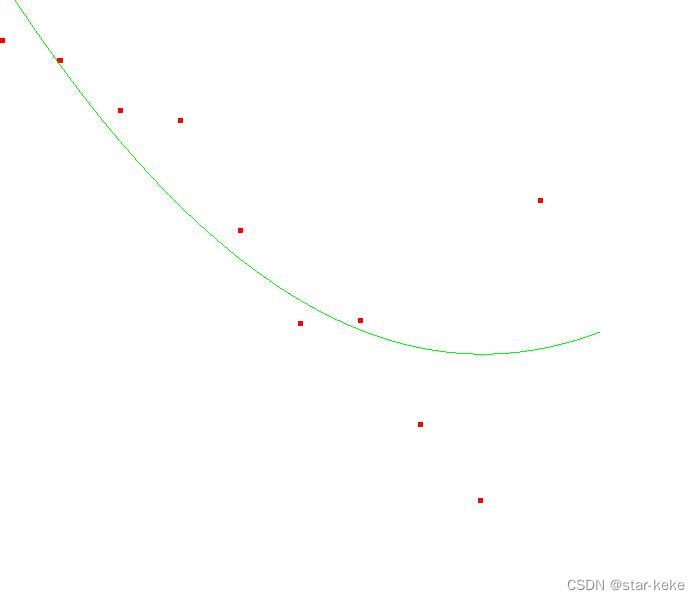
5阶多项式：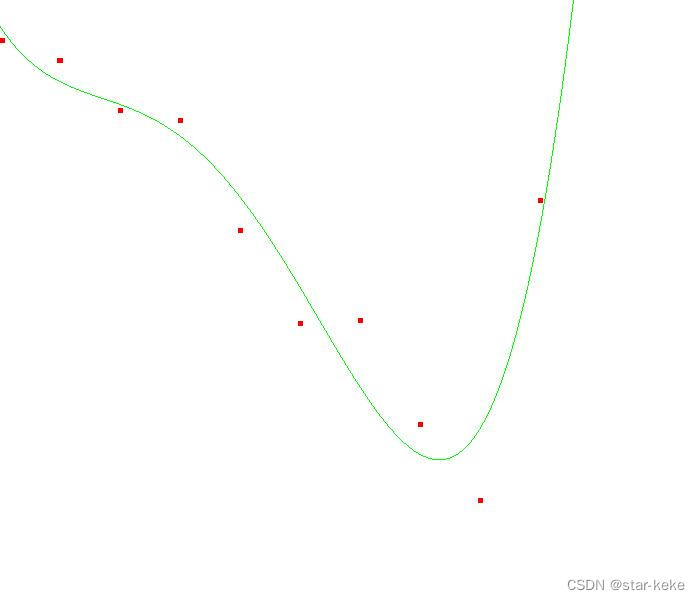

7阶多项式：

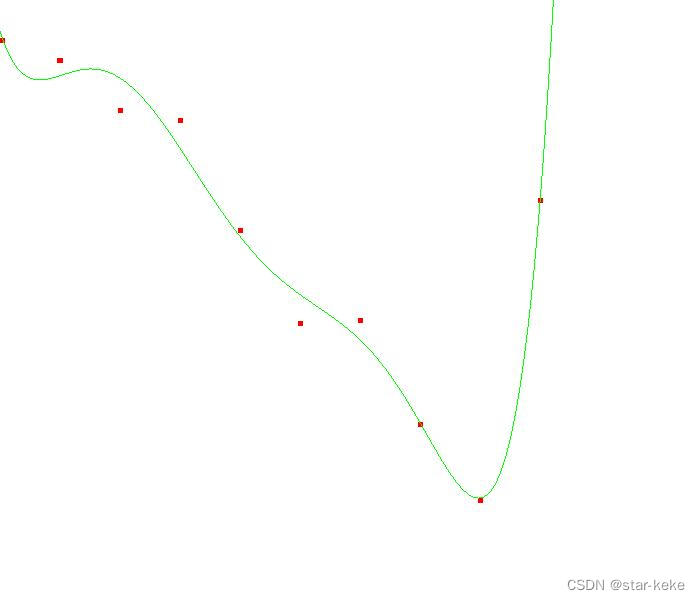
平面拟合： 

 平面方程：Ax+By+Cz+D=0

//z = A*x + B*y + C
void Least_squares_plane(double input[][3], int number, double& A, double& B, double& C)
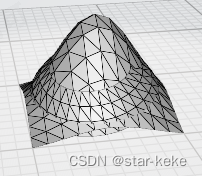
{Eigen::MatrixXd MatX;Eigen::MatrixXd MatY;MatX.resize(number, 3);MatY.resize(number, 1);Eigen::MatrixXd MatLS;MatLS.resize(number, 1);for (int i = 0; i < number; ++i) {MatX.row(i) = Eigen::RowVector3d(input[i][0], input[i][1],1);MatY.row(i)[0] = input[i][2];}MatLS = (MatX.transpose() * MatX).inverse() * MatX.transpose() * MatY;A = MatLS(0, 0);B = MatLS(1, 0);C = MatLS(2, 0);}

以该3D模型的每个三角形面片的顶点为观测数据：

拟合的平面如下：

高斯拟合：

 高斯函数

 

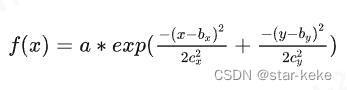
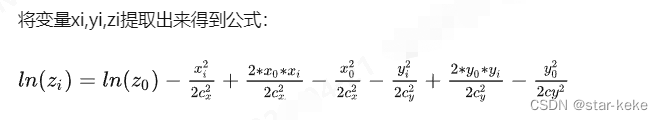
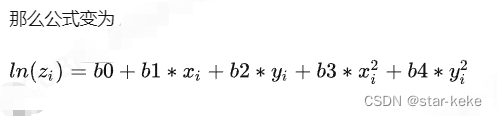
//ln(z) = A + B*x + C*y + D*x*x + E*y*y
//z = exp(A + B*x + C*y + D*x*x + E*y*y)
void Least_squares_gaussian(double input[][3], int number, double& A, double& B, double& C, double& D, double& E)
{Eigen::MatrixXd MatX;Eigen::MatrixXd MatY;MatX.resize(number, 5);MatY.resize(number, 1);Eigen::MatrixXd MatLS;MatLS.resize(number, 1);for (int i = 0; i < number; ++i) {Eigen::Matrix<double, 5, 1> row;row << 1 , input[i][0] , input[i][1] , input[i][0] * input[i][0] , input[i][1] * input[i][1];MatX.row(i) = row;MatY.row(i)[0] = log(input[i][2]);}MatLS = (MatX.transpose() * MatX).inverse() * MatX.transpose() * MatY;A = MatLS(0, 0);B = MatLS(1, 0);C = MatLS(2, 0);D = MatLS(3, 0);E = MatLS(4, 0);
}

同样以该3D模型的顶点为观测数据

拟合高斯面如下：