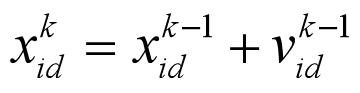PSO优化问题

article/2025/10/26 0:24:09

PSO

import matplotlib.pyplot as plt
import numpy as np
import random as rd
np.set_printoptions(precision=3,suppress=True)class PSO():"""用于求解最小值"""def __init__(self,pop_scale,dim,maxV,pop_bnd,maxiter):self.pop_scale = pop_scale#种群规模self.dim = dim#X解的维度self.maxiter = maxiter#种群迭代次数self.popx = np.zeros((self.pop_scale,self.dim))#种群位置存储self.popv = np.zeros((self.pop_scale, self.dim))#种群速度存储self.maxV = maxV#速度最大变化值self.pop_bnd = pop_bnd#X的约束范围self.c1 = 2#更新速度所用的参数c1self.c2 = 2#更新速度所用的参数c2self.w  = 0.4#0.4/0.9 值不同收敛速度和局部搜索能力不同self.p_history_values = np.zeros((1,self.pop_scale)).reshape(-1)#记录每一个粒子的y变化的最优值self.p_best = np.zeros((self.pop_scale,dim))#记录每一个粒子的y变化的最优位置self.g_history_values = np.zeros((1, 1)).reshape(-1)  # 记录全局最优值self.g_best = np.zeros((self.pop_scale, dim))  # 记录全局最优位置self.g_values = []#记录每次迭代的结果self.all_pop = []def y_values(self,X):#目标函数a = np.power(X,2)b = np.ones((1,a.shape[1]))###sum(X^2)return np.dot(a,b.T)
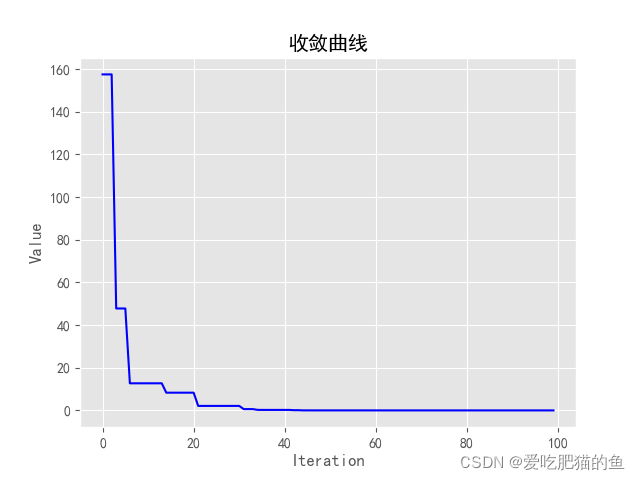
#'——————————————————————————————————初始化————————————————————————————————————————'def inti_pop(self):#初始化种群"""经数据验证初始化初始化程序无误"""self.popx = np.random.uniform(self.pop_bnd[0],self.pop_bnd[1],size=(self.pop_scale,self.dim))#初始化种群位置self.popv = np.random.uniform(0,self.maxV,size=(self.pop_scale,self.dim))#初始化种群速度self.p_history_values =  self.y_values(self.popx)#记录种群个体最优值p_yself.p_best = self.popx#记录种群个体位置最优，初次迭代所以等于popxself.g_best = self.p_best[self.p_history_values.tolist().index(self.p_history_values.max())]#全局最优位置self.g_history_values = self.y_values(np.array([self.g_best]))#全局最优位置的函数值g_ydef plot(self):#绘制收敛曲线plt.rcParams['font.sans-serif'] = 'simhei'plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号plt.style.use('ggplot')plt.title("收敛曲线")plt.plot(np.array(self.g_values).reshape(-1),color='blue')plt.ylabel('Value')plt.xlabel('Iteration')plt.savefig('./收敛曲线.png')plt.show()bird = np.array(self.all_pop)fig, [ax1,ax2 ]= plt.subplots(nrows=2, ncols=1)#, figsize=(20, 8)ax1.plot(bird[:, :, 0])ax1.set_ylabel('x-Value')ax1.set_xlabel('x-Iteration')ax2.plot(bird[:, :, 1])ax2.set_ylabel('y-Value')ax2.set_xlabel('y-Iteration')plt.tight_layout(h_pad=2,)plt.savefig('./xy收敛曲线.png')plt.show()def bound(self):#防止X超出约束边界for i in range(self.popx.shape[0]):for j in range(self.popx.shape[1]):if self.popx[i][j] > self.pop_bnd[0]:self.popx[i][j] = self.pop_bnd[0]if self.popx[i][j] < self.pop_bnd[1]:self.popx[i][j] = self.pop_bnd[1]
#'——————————————————————————————————开始迭代计算————————————————————————————————————'def pso(self):for cycle in range(self.maxiter):# 更新速度 ，开始下一种群迭代，产生新种群self.popv = self.w*self.popv + \self.c1*rd.random()*(self.p_best) +\self.c2*rd.random()*(self.g_best*np.ones_like(self.popx)-self.popx)self.popx = self.popx +self.popv#粒子群新的位置##缺少边界约束，# self.bound()value = self.y_values(self.popx)  # 新一代粒子群的y值for i in range(self.pop_scale):#更新b_best 和g_bestif self.p_history_values[i]>value[i]:self.p_history_values[i]=value[i]#更新历史最优yself.p_best[i] = self.popx[i]#更新粒子历史最优位置if self.p_history_values[i]<self.g_history_values:self.g_history_values = self.p_history_values[i] #更新全局最优gself.g_best = self.p_best[i]#更新全局最优位置self.g_values.append(self.y_values(np.array([self.g_best])))#记录每次迭代的计算结果值self.all_pop.append(self.popx)self.plot()#收敛曲线if __name__=='__main__':opt = PSO(pop_scale=20,dim=100,maxV=2,pop_bnd=(-2,2),maxiter=100)opt.inti_pop()opt.pso()print(f'最优值f(x):\n {opt.g_history_values}\n')print(f'最优解   x:\n{opt.p_best[-1]}')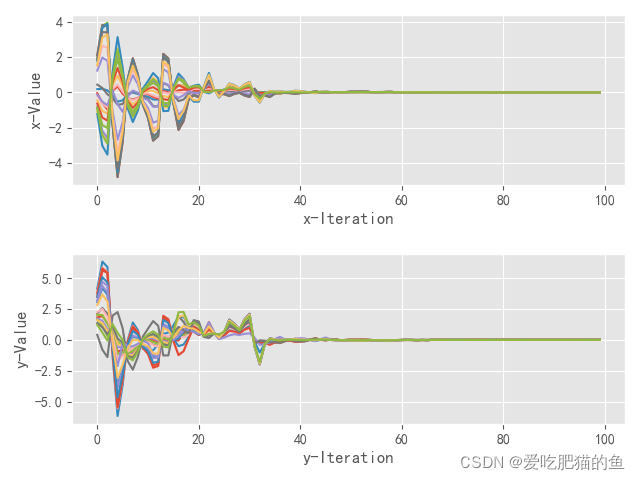

任意两个维度数的收敛情况
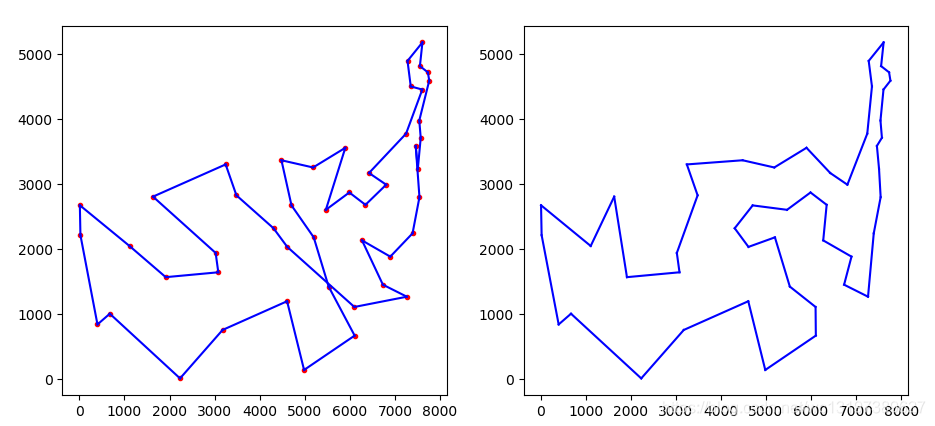
在这里插入图片描述对于5个维度以下的解 还算还可以，维度太高，求解不是和精确，
可能与参数选取有关
在这里插入图片描述

Example2：
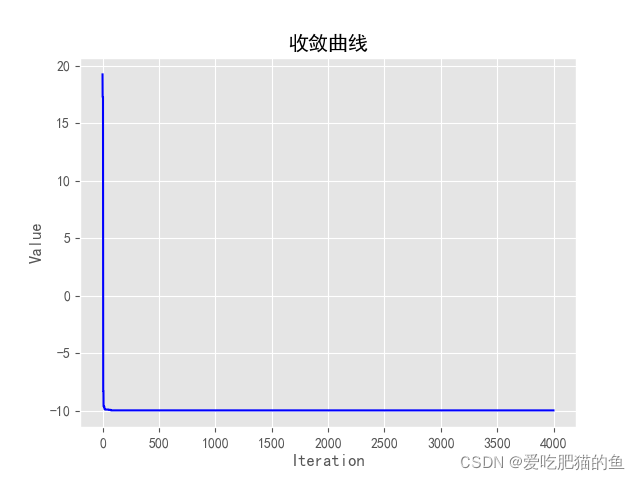
求解：np.arctan(X)/(np.sin(X)+1.1) 可以看出 收敛值在pi/2 *10 左右 约为15.70

import matplotlib.pyplot as plt
import numpy as np
import random as rd
# np.set_printoptions(precision=3,suppress=True)class PSO():"""用于求解最小值"""def __init__(self,pop_scale,dim,maxV,pop_bnd,maxiter):self.pop_scale = pop_scale#种群规模self.dim = dim#X解的维度self.maxiter = maxiter#种群迭代次数self.popx = np.zeros((self.pop_scale,self.dim))#种群位置存储self.popv = np.zeros((self.pop_scale, self.dim))#种群速度存储self.maxV = maxV#速度最大变化值self.pop_bnd = pop_bnd#X的约束范围self.c1 = 2#更新速度所用的参数c1self.c2 = 2#更新速度所用的参数c2self.w  = 0.4#0.4/0.9 值不同收敛速度和局部搜索能力不同self.p_history_values = np.zeros((1,self.pop_scale)).reshape(-1)#记录每一个粒子的y变化的最优值self.p_best = np.zeros((self.pop_scale,dim))#记录每一个粒子的y变化的最优位置self.g_history_values = np.zeros((1, 1)).reshape(-1)  # 记录全局最优值self.g_best = np.zeros((self.pop_scale, dim))  # 记录全局最优位置self.g_values = []#记录每次迭代的结果self.all_pop = []def y_values(self,X):#目标函数# a = np.power(X,1)*(X-2)# b = np.ones((1,a.shape[1]))# return np.dot(a,b.T)return np.arctan(X)/(np.sin(X)+1.1)
#'——————————————————————————————————初始化————————————————————————————————————————'def inti_pop(self):#初始化种群"""经数据验证初始化初始化程序无误"""self.popx = np.random.uniform(self.pop_bnd[0],self.pop_bnd[1],size=(self.pop_scale,self.dim))#初始化种群位置self.popv = np.random.uniform(0,self.maxV,size=(self.pop_scale,self.dim))#初始化种群速度self.p_history_values =  self.y_values(self.popx)#记录种群个体最优值p_yself.p_best = self.popx#记录种群个体位置最优，初次迭代所以等于popxself.g_best = self.p_best[self.p_history_values.tolist().index(self.p_history_values.max())]#全局最优位置self.g_history_values = self.y_values(np.array([self.g_best]))#全局最优位置的函数值g_ydef plot(self):#绘制收敛曲线plt.rcParams['font.sans-serif'] = 'simhei'plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号plt.style.use('ggplot')plt.title("收敛曲线")plt.plot(np.array(self.g_values).reshape(-1),color='blue')plt.ylabel('Value')plt.xlabel('Iteration')plt.savefig('./收敛曲线.png')plt.show()# bird = np.array(self.all_pop)# fig, [ax1,ax2 ]= plt.subplots(nrows=2, ncols=1)#, figsize=(20, 8)# ax1.plot(bird[:, :, 0])# ax1.set_ylabel('x-Value')# ax1.set_xlabel('x-Iteration')# ax2.plot(bird[:, :, 1])# ax2.set_ylabel('y-Value')# ax2.set_xlabel('y-Iteration')# plt.tight_layout(h_pad=2,)# plt.savefig('./xy收敛曲线.png')# plt.show()def bound(self):#防止X超出约束边界for i in range(self.popx.shape[0]):for j in range(self.popx.shape[1]):if self.popx[i][j] > self.pop_bnd[0]:self.popx[i][j] = self.pop_bnd[0]if self.popx[i][j] < self.pop_bnd[1]:self.popx[i][j] = self.pop_bnd[1]
#'——————————————————————————————————开始迭代计算————————————————————————————————————'def pso(self):gg_value = self.g_history_valuesfor cycle in range(self.maxiter):# 更新速度 ，开始下一种群迭代，产生新种群self.popv = self.w*self.popv + \self.c1*rd.random()*(self.p_best) +\self.c2*rd.random()*(self.g_best*np.ones_like(self.popx)-self.popx)self.popx = self.popx +self.popv#粒子群新的位置##缺少边界约束，# self.bound()value = self.y_values(self.popx)  # 新一代粒子群的y值for i in range(self.pop_scale):#更新b_best 和g_bestif self.p_history_values[i]>value[i]:self.p_history_values[i]=value[i]#更新历史最优yself.p_best[i] = self.popx[i]#更新粒子历史最优位置if self.p_history_values[i]<self.g_history_values:self.g_history_values = self.p_history_values[i] #更新全局最优gself.g_best = self.p_best[i]#更新全局最优位置self.g_values.append(self.y_values(np.array([self.g_best])))#记录每次迭代的计算结果值# self.all_pop.append(self.popx)self.plot()#收敛曲线if __name__=='__main__':opt = PSO(pop_scale=10,dim=1,maxV=2,pop_bnd=(-9,9),maxiter=4000)opt.inti_pop()opt.pso()print(f'最优值f(x):\n {opt.g_history_values}\n')print(f'最优解   x:\n{opt.p_best[-1]}')print(np.pi/2)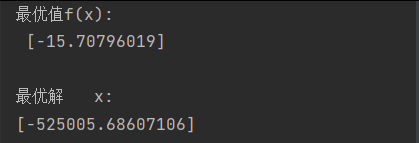

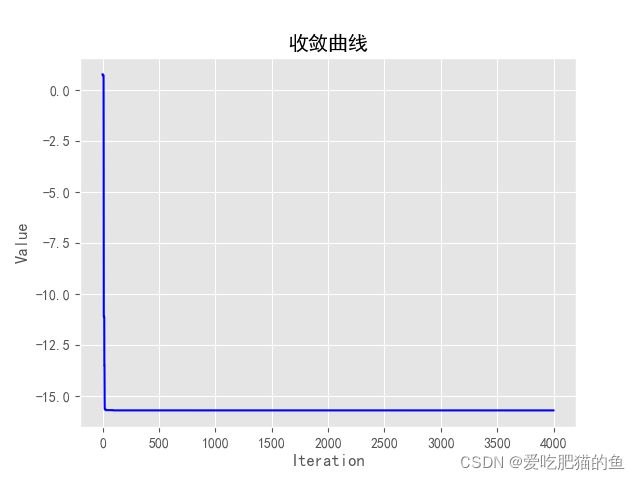在这里插入图片描述
在这里插入图片描述200次以内就已经收敛了，
但是
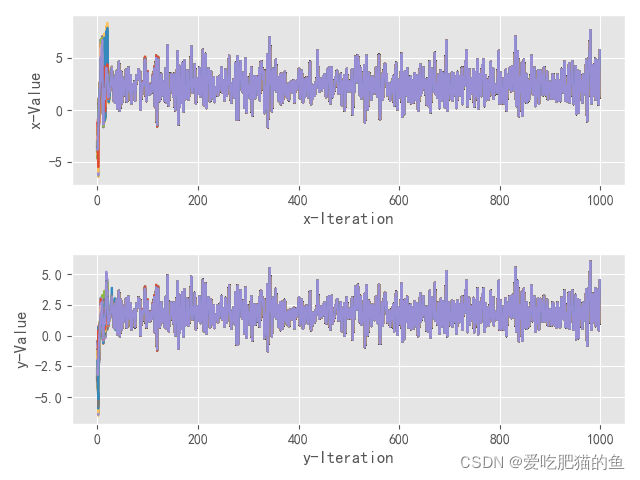在这里插入图片描述对于解集中的任意一个Xi来说并没有收敛，这是一个问题

存在问题：

  • 维度过高时，计算不是很准确，存在1-5范围内的误差
  • 改进：限制后期的速度变化。参考模拟退火T逐渐下降
  • X的边界约束限制问题。这里没有约束限制，约束方法需要进一步确定

http://chatgpt.dhexx.cn/article/Pcb5scM3.shtml

相关文章

利用PSO求解TSP问题

利用PSO求解TSP问题

简介 PSO(粒子群算法)是群智能算法的一种&#xff0c;其他的群智能算法还有蚁群算法&#xff0c;遗传算法等。其他的智能算法还有模拟退火。之前看过一段时间的PSO&#xff0c;商务智能课程最后的大作业便想用一下&#xff0c;刚好在github上看到有人用模拟退火解决TSP…
阅读更多...
【PSO】PSO原始算法

【PSO】PSO原始算法

PSO粒子群优化算法由由Kennedy和Eberhart于1995年提出。模拟鸟集群飞行觅食的行为&#xff0c;鸟之间通过集体的协作使群体达到最优目的。 每个寻优的问题解都被想像成一只鸟&#xff0c;称为“粒子”。所有粒子都在一个D维空间进行搜索。 所有的粒子都由一个fitness function…
阅读更多...
【PSO运输优化】基于MATLAB的PSO运输优化算法的仿真

【PSO运输优化】基于MATLAB的PSO运输优化算法的仿真

1.软件版本 matlab2013b 2.本算法理论知识 问题是&#xff0c;假设我有一个收集轨道&#xff0c;上面有5个采集堆&#xff0c;这5个采集堆分别被看作一个4*20的矩阵&#xff08;下面只有4*10&#xff09;&#xff0c;每个模块&#xff08;比如&#xff1a;A31和A32的元素含量…
阅读更多...
粒子群算法（PSO）

粒子群算法（PSO）

理论&#xff1a; 粒子群优化算法&#xff08;PSO&#xff09;是一种智能优化算法&#xff0c;也是一种元启发式算法&#xff0c;最初是由Eberhart和Kennedy提出的&#xff0c;其模拟了鸟群捕食行为&#xff0c;通过一定的搜索策略&#xff0c;使得多个粒子在多维搜索空间中寻…
阅读更多...
粒子群算法（PSO）简介及Python实现

粒子群算法（PSO）简介及Python实现

一、概述 粒子群算法&#xff0c;也称粒子群优化算法或鸟群觅食算法(Particle Swarm Optimization) &#xff0c;缩写为PSO.粒子群优化算法是一种进化计算技术(evolutionary computation)&#xff0c;1995年由Eberhart博士和kennedy 博士提出&#xff0c;源于对鸟群捕食的行为研…
阅读更多...
mac中如何在PS中使用Cutterman工具快速切图

mac中如何在PS中使用Cutterman工具快速切图

简介 cutterman是安装在PS软件中的一款智能自动切图插件&#xff0c;用法简单方便&#xff0c;很受设计者们喜欢&#xff0c;导出的图片格式有多种选择&#xff0c;而且还可以针对不同机型选择如苹果系统、安卓系统或电脑端使用。 工具/原料 Photoshoppsd格式图层图片 方法/…
阅读更多...
sketch android 切图,Sketch如何快速切图？三分钟教你掌握切图方案

sketch android 切图,Sketch如何快速切图？三分钟教你掌握切图方案

相信有相当一部分的设计同行在工作中碰到各种各样切图尺寸大小的问题&#xff0c;针对Sketch如何快速切图这个问题&#xff0c;今天小编特意出了一篇有关sketch切图尺寸教程的文章&#xff0c;学会了包你三分钟之内掌握设置切图方案的技巧&#xff0c;然后更安心的把剩余时间花…
阅读更多...
切图教程，app切图命名总结

切图教程，app切图命名总结

再根据自己的习惯对APP切图命名进行整理总结。 结语&#xff1a; 作为一个有强迫症的设计师&#xff0c;希望产出是有缜密的思维逻辑&#xff0c;当然包括细节。 文字有的部分参考其它文章&#xff0c;整理后根据自己的工作经验作出的总结。 自己也还在不断的摸索与学习。 声明…
阅读更多...
PS切图方法

PS切图方法

方法一&#xff1a;直接右击选中图层&#xff0c;另存为.png文件 方法二&#xff1a;对于分离的几个图层&#xff0c;右击shift选中&#xff0c;ctrE合并图层&#xff0c;再用方法一 方法三&#xff1a;利用切片工具进行切图&#xff1a; 方法四&#xff1a;PS插件切图&#…
阅读更多...
PS中的切图

PS中的切图

文章目录 图层切图切片切图PS插件切图附&#xff1a;常见的图片格式 PS 有很多的切图方式&#xff1a;图层切图、切片切图、PS 插件切图等。 图层切图 最简单的切图方式&#xff1a;右击图层 --> 导出 PNG 切片。 如果发现某张图片它的文字和背景是分离的&#xff0c;那么…
阅读更多...
真正的ps切图方法（前端必看）

真正的ps切图方法（前端必看）

看了很多ps切图方法&#xff0c;真的感觉都不是很满意&#xff0c;可能说不是很合适我们前端的用法&#xff0c;毕竟我们要获取的是某一个图层里面的小图片&#xff0c;不需要获取全部切图&#xff0c;好了&#xff0c;废话不多说&#xff0c;看方法。 1.选中所在的图层&#x…
阅读更多...
ps 快速切图

ps 快速切图

前端实战系列之---两种快速切图的方法 今天给大家分享一下我自己在前端工作中的一些切图小技巧&#xff0c;虽然好的UI会给我们把图切好&#xff0c;但是他们切的图不一定百分之百符合我们的需求&#xff0c;所以还是自己动手丰衣足食嘛&#xff0c;看本教程之前希望大家能先看…
阅读更多...
切图工具：又一个处理大图的例子

切图工具：又一个处理大图的例子

工具下载 有些同学对处理大图还是不太明白&#xff0c;这里再仔细写一个例子&#xff0c;希望能有所帮助。 基本情况&#xff1a; 1、使用高德地图&#xff1b; 2、朋友使用12级地图截屏做底图&#xff0c;制作的源图为17级&#xff0c;分辨率为40960*40960&#xff1b; 由于…
阅读更多...
地图切图工具：初步实现顺序法批量切图处理，用于处理大图

地图切图工具：初步实现顺序法批量切图处理，用于处理大图

工具&#xff1a;https://blog.csdn.net/bq_cui/article/details/47372005 &#xff08;20190504&#xff09; 由于技术限制&#xff0c;本工具无法打开超级大图。切图时如果遇到一个很大的源图片&#xff0c;工具会难以处理&#xff0c;一般是跳出内存溢出提示&#xff0c;点击…
阅读更多...
houdini 之copy to points

houdini 之copy to points

将第一个输入中的几何图形复制到第二个输入的点上。 属性备注Source Group几何体来源Target Points要复制到的目标点集合Show Guide Geometry是否显示该操作预览流程Pack and Instance在复制之前将输入几何体打包到嵌入式打包图元中。这导致输入几何被每个副本共享&#xff08;…
阅读更多...
如何利用Photoshop进行快速切图

如何利用Photoshop进行快速切图

在UI设计中我们常常使用Ai来进行矢量图的绘制&#xff0c;然后导入Ps中进行设计、排版和导出。 在以前的版本中&#xff0c;切图一直是个很麻烦的事情&#xff0c;要么依托于脚本&#xff0c;要么手动一张张导出&#xff0c;很不方便&#xff0c;这种窘况在Photoshop CC 2015…
阅读更多...
图像分割之图割（Graph Cut）

图像分割之图割（Graph Cut）

基本概念 这里介绍一种用于n维图像数据的边界优化和区域分割的分割技术。该分割算法来自论文&#xff1a;Interactive Graph Cuts for Optimal Boundary & Region Segmentation of Objects in N-D Images。该方法通过交互式的或自动的定位一个或多个代表“物体”的点以及一…
阅读更多...
4. PS切图

4. PS切图

4.1常见的图片格式 jpg图像格式: JPEG ( .JPG )对色彩的信息保留较好,高清,颜色较多,我们产品类的图片经常用jpg格式的gif图像格式 : GIF格式最多只能储存256色,所以通常用来显示简单图形及字体,但是可以保存透明背景和动画效果,实际经常用于一些图片小动画效果png图像格式&am…
阅读更多...
Photoshop 实时切图功能 Generate

Photoshop 实时切图功能 Generate

大家好&#xff0c;我是笨笨&#xff0c;笨笨的笨&#xff0c;笨笨的笨&#xff0c;谢谢!!! 本文发表在【湖边的小屋遗址】 转载请注明出处 Generate web assets in Photoshop CC 貌似就是以前的 Ctrl Shift Alt s 升级。并不只是操作上&#xff0c;感觉是要优化输出资源的…
阅读更多...
IOS切图直接作为Android切图使用

IOS切图直接作为Android切图使用

跳槽到新公司之后&#xff0c;发现工作真心挺坑的&#xff0c;基本没什么流程规范&#xff0c;职责分工也不明确&#xff0c;整天瞎折腾。。。&#xff0c;慢慢的开始怀念起老东家了。 在新公司UI只提供ios的切图给开发&#xff0c;其实他们不会做android切图。。。&#xff0c…
阅读更多...
推荐文章

Copyright @ 2022~2023