PSO粒子群优化算法由由Kennedy和Eberhart于1995年提出。模拟鸟集群飞行觅食的行为,鸟之间通过集体的协作使群体达到最优目的。
- 每个寻优的问题解都被想像成一只鸟,称为“粒子”。
- 所有粒子都在一个D维空间进行搜索。 所有的粒子都由一个fitness function 确定适应值以判断目前的位置好坏。
- 每一个粒子必须赋予记忆功能,能记住所搜寻到的最佳位置。
- 每一个粒子还有一个速度以决定飞行的距离和方向。这个速度根据它本身的飞行经验以及同伴的飞行经验进行动态调整。
PSO优化算法中每个粒子下一步的移动方向都结合了惯性,自己的历史最优位置,和种群历史最优位置。算法前期倾向于个体自由探索,后期逐渐收敛于群体最优解。
我们定义适应度函数为f(x),粒子群优化算法每个粒子可以看作是空间中的1个点,求解参数的维度(问题空间)是N,那么第i个粒子的位置Xi就是一个N维的向量,它的速度Vi也是一个N维的向量。粒子下一时刻的位置=当前位置+当前速度向量。
粒子当前时刻的速度更新公式:
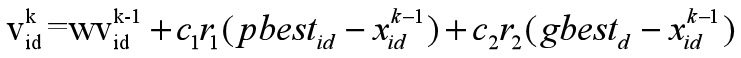
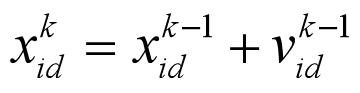
- w是惯性系数,非负数
- V(k,id)—第k次迭代粒子i飞行速度矢量的第d维分量
- X(k,id) —第k次迭代粒子i位置矢量的第d维分量
- c1,c2加速度常数,调节学习最大步长
- r1,r2—两个随机函数,取值范围[0,1],以增加搜索随机性
算法流程图:
- 初始化粒子群
- 计算每个粒子的适应度
- 更新V和X
- 判断是否到达算法退出条件,否则跳至2
- 退出
代码的python实现:
class PSO():# 粒子群初始化def __init__(self, pN, dim, max_iter):self.w = 0.3self.c1 = 0.2self.c2 = 0.2self.r1 = 0.1self.r2 = 0.1self.pN = pN # 粒子数量self.dim = dim # 搜索维度self.max_iter = max_iter # 迭代次数self.limit = limit# 初始化粒子群self.X = np.random.random((pN, dim))self.V = np.zeros_like(self.X)self.pbest = self.Xself.gbest = self.X[0] # 先假设第1颗粒子是最好的位置self.p_fit = np.ones(self.pN) * float('-inf')self.fit = float('-inf') # 全局最佳适应值,初始化为负无穷self.fit_function = fitness_functiondef iterator(self):# 更新粒子群位置for epoch in range(self.max_iter):# 更新gbest/pbestfor i in range(self.pN): score = self.fit_function(self.X[i])if (score > self.p_fit[i]): # 更新个体最优self.p_fit[i] = scoreself.pbest[i] = self.X[i]if (score > self.fit): # 更新全局最优best_particle = iself.gbest = self.X[i]self.fit = self.p_fit[i]# 更新粒子群位置for i in range(self.pN):self.V[i] = self.w * self.V[i] + self.c1 * self.r1 * (self.pbest[i] - self.X[i]) + \self.c2 * self.r2 * (self.gbest - self.X[i])self.X[i] += self.V[i]