定点数与浮点数

• 所谓定点数就是指小数点的位置固定不变
• 而浮点数是小数点的位置是不固定的，会浮动

1 ) 定点数

• 用熟悉的十进制数来类比，定点数就是我们平时更习惯使用的常规的计数方式，我们会显式的标明小数点的位置
• Eg: 110.12

2 ） 浮点数

• 浮点数呢，就是我们用科学计数法表示的这种数
• Eg: $2.2353\ast 10^2$
  • 虽然我们把小数点的位置标注在了这个地方，但是如果在乘上我们给出的这个阶码
  • 小数点其实是会往后移的，那这是我们熟悉的十进制，其实对于二进制也是类似的

3 ) 类比二进制

• 二进制的数据表示也分为定点数和浮点数，虽然都是0101组成的, 但我们终归需要确定这个小数点的一个位置
• 如果我们规定小数点的位置固定不变，这就是定点数，如果我们还需要加上一个类似于科学计数法的这种阶码，那么这种数就是浮点数

定点数的表示

• 定点数分为无符号数和有符号数，其中有符号数可以用原码、反码、补码、移码这样的四种方式来表示
• 我们需要重点关注这几种码之间的相互转换问题

无符号数

• 所谓无符号数就是指整个机器字长的全部二进制位都是用来表示数值，并没有正负这样的符号之分，相当于我们使用所有的二进制位来表示数的绝对值
• 比如像这个二进制数：1001 1100B，它所对应的十进制就应该是156D，
• 转换原理就是用每一位二进制数乘以这一位的位权，然后所有的位进行一个相乘相加就可以
• 无符号数的表示范围是多大？
  • 先确定一个前提条件，就是我们到底用多少个比特位来表示一个无符号数
  • 位数越多，显然表示的范围越大。比如我们使用八位二进制来表示一个无符号数，那么八位二进制总共可以有二的八次方种状态
  • 分别是 0000 0000 ~ 1111 1111，那所有的二进制位都为1，这个二进制数所对应的真值应该是多少呢？是 $2^8-1$ 即 255
  • 我们可以把每一位和位权相乘相加，那八个二进制位就相当于是 $2^7+2^6+...+2^1+2^0$ 这个等比数列的求和套用公式
  • $S_n=a_1\ast \frac{1-q^n}{1-q}=2^8-1=255$
• 再换一种思路来算8个1所表示的值
  • 现在我们给这八个1再加上一个1，那么末位1加1等于0，向高位进1
  • 1加1又等于0，再向高位进1，好，那所有的这些都是等于0进1
  • 最后我们会往更高位再进一个1，那更高的这个位它的权值应该是二的八次方
  • 因为它是第九个二进制位，所以如果我们在原先这个值的基础上加一等于二的八次方
  • 那么原本的这个值不就是二的八次方减一吗？所以我们也可以用这样的思路来确定八个一它所表示的一个值
• 如果把刚才这种思路再进行一个推广的话，N位的无符号数它能表示的范围显然就应该是零到二的N次方减一, 这是N位无符号数的一个表示范围。
• 所有的二进制位都是用来表示数值，而没有符号位，所以称为无符号数
• 一般来说，当我们谈到无符号数的时候，我们通常只会讨论无符号的整数，而没有无符号的小数
• 比如在学习C语言的时候，它有一个关键字叫unsigned，这个关键字你只能用来修饰 unsigned int 或者long这些整数相关的
• 如果用unsigned去修饰float这种浮点数的话，那它的编译器是会报错的，所以当我们在谈到这种无符号数的时候，通常我们只会探讨整数，无符号的整数，而不会探讨小数。

有符号数

• 对于有符号数来说，我们既需要考虑到整数如何表示，也需要考虑到小数如何表示
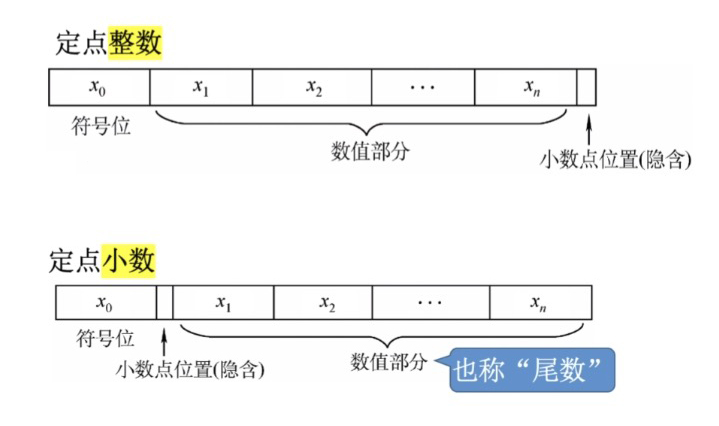
• 那如果要表示整数的话，我们通常会规定小数点是固定的，隐含在最低位的后面，然后最高位的这个二进制位表示的是符号位，（通常0表示的是正，然后1表示的是负)
• 如果我们用定点的方式表示小数的话，我们通常会规定最高位为符号位，小数点隐含在这个符号位的后面
• 因此如果我们用这种定点的方式来表示一个比如说是19.75这样的数的话，那我们需要把整数部分单独的保存，然后把小数部分单独的保存
• 我们可以用原码、反码、补码这样的三种方式来表示定点的整数或者小数，另外还可以用移码来表示定点的整数
• 若真值记为x的话，那我们会用这种x加一个中括号，然后右下角标注原、反、补、移这样的方式来表示x所对应的原码、反码、补码和移码
• 示例：$[x{]}_{原}$、$[x{]}_{反}$、$[x{]}_{补}$、$[x{]}_{移}$
• 还有一个概念叫做尾数，就是指我们用来表示整数或者小数的数值部分的二进制位，我们就把它称为尾数，然后最高位我们把它称为符号位

原码

定点整数

• 原码就是指我们会用尾数来表示真值的绝对值，其实就是之前我们一直在探讨的大家比较熟悉的那种二进制数表示方法
• 我们假设机器字长是8位，也就是说我们有一位用来表示符号，然后剩下的七位用来表示数值，也就是尾数。
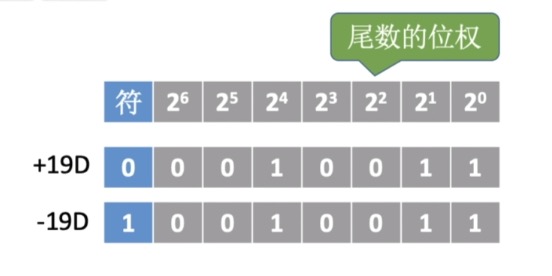
• 首先来看一下定点整数用原码怎么来表示，每一个定点整数占八个比特位，最高位是符号，后续每一个位的权值如上图
• 如果说我们要用原码的方式表示正的19的话，首先符号为正号，应该是对应零
• 然后后续的这七个尾数我们需要表示成这个真值的绝对值，也就是19， 19 = 16 + 2 + 1, 即：10011
• 所以19的尾数就应该是0010011，写全就是：00010011
• 如果我们要表示的是负19的话，只需要把符号位从0变为1就可以了, 这就是19和负19的一个原码表示
• 注意我们的定点整数的小数点是默认隐含在了最后面的位置
• 所以我们才可以确定右手边第一位的位权是二的零次方，再往上一位是二的一次方 …
• 我们规定小数点隐含在哪个位置，左手边就是二的一次方，右手边就是二的负一次方，依次类推
• 所以我们确定各个位的权值是基于我们小数点的隐含位置来进行判断的
• 注意：如果要求计算我们的这个定点整数它需要占多少位，那么我们需要把高位的部分补上零

定点小数

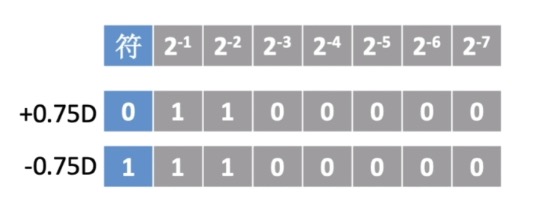
• 由于我们的小数点是隐含在了符号位的后面，所以小数点右边这位权值应该是二的负一，往后是二的负二，负三啊，一直到二的负七
• 即：第一位是0.5，第二位是0.25，第三位是0.125，…
• 正的0.75怎么表示呢？0.75应该刚好是等于0.5加上0.25，所以尾数部分肯定是两个1，然后后续全部是0
• 那正的0.75我们只需要让符号位为零就可以，即：01100000
• 而负的0.75我们把符号位从0改成1，然后尾数依然是不变，即：11100000
• 这就是定点小数的一个原码表示
• 同样的，如果告诉我们机器字长的位数, 比如是8，或者指明了源码需要占多少位, 那么我们有可能需要在后面补一些零，凑足规定的位数
• 常见这样一种书写方式：$[x{]}_{原}=1,0010011$, 就是有的地方可能会在符号位后面打一个小小的逗号，但是这个逗号其实是不存在的，是我们脑补上去的
• 这么写只不过是为了更好的区分符号位还有尾数这样的两个部分, 另外如果没有明确的指明机器字长是多少，原码需要占多少位
• 那么像刚才-19这个数我们也可以写成: $[x{]}_{原}=1,10011$ 即符号位后面的尾数中间补上的0可以给抹去
• 同理，表示定点小数的时候，也可以写成这样的一种形式：$[x{]}_{原}=1.1100000$ 注意左边第一个1是符号，.是小数点，这个数理解为：-0.11

原码的表示范围

1 ) 原码表示定点整数的一个表示范围

• 总共有n+1位，其中尾数有N位，那么N位的尾数可以表示的绝对值的范围应该是零到二的N次方减一
• 那我们再加上符号位的话，最小的我们可以表示的整数就应该是负的2N次方减一，而正的可以表示的最大整数就应该是二的N次方减一
• 即：$-(2^n-1)\le x\le 2^n-1$ 关于原点对称
• 注意: 用原码表示定点整数，在表示真值零的时候，可以有+0和-0这样的两种形式
  • 正零就是符号位为零，然后后续的尾数也全部是零
  • 而负零就是符号位为一，后续的尾数全部是零
• 因此虽然n+1个二进制位可以表示出二的n+1次方这么多种状态, 理论上我们也可以表示出这么多个数
• 但实际上在这个范围内其实只包含了二的N次方加一，然后再减一这么多个数, 即：$2^{n+1}-1$, 原因就是其中的两个二进制状态对应了同一个真值

2 ) 原码表示定点小数的一个表示的范围

• 总共n+1位，其中一个位表示符号，后边的N位表示实际的数值，那么这N个二进制位所能表示的绝对值的范围：最小是零，就是所有都是零，然后最大的话就是所有都是1
• 即：$02^{-1}+2^{-2}+...+2^{-n}$，也就是 $01-2^{-n}$， 如果再加上符号为正负的话
• 那它所能表示的最小值就应该是这样的一个值，$-(1-2^{-n}\le x\le 1-2^{-n}$
• 同样，在表示真值零的时候，同样也可以有正零和负零这样的两种形式

反码

• 反码其实很简单，当我们得到原码之后，可以判断，如果说原码的符号位为零，也就是是一个正数，那么反码和原码其实是相同的

• 而如果说符号位为1，那么我们只需要在原码的基础上把数值位全部取反就可以

• 比如像刚才正19这个数，它的原码如下，那由于此时符号位为零，它是一个正数，所以这个数的反码表示和原码表示是一样的

  • x = + 19D
    • $[x{]}_{原}=0,0010011$
    • $[x{]}_{反}=0,0010011$

• 而负19这个数由于符号位为1，所以我们需要把后边的这些数值位在原码的基础上全部取反

  • x = - 19D
    • $[x{]}_{原}=10010011$
    • $[x{]}_{反}=11101100$

• 再来看小数的举例

  • x = +0.75D
    • $[x{]}_{原}=0.1100000$
    • $[x{]}_{反}=0.1100000$
  • x = -0.75D
    • $[x{]}_{原}=1.1100000$
    • $[x{]}_{反}=1.0011111$

• 以上就是定点整数和定点小数的反码表示，我们需要先得到原码，然后再转变成反码

• 那显然反码和原码之间是有这种一一对应的关系的，所以n+1位的反码整数，它的表示范围和原码肯定也是一致的

• 同样的反码也会拥有负零和正零这样的两种形式，原码的正零是全为零，那反码的正零也是全部为零

• 原码的负零是首位为1，后边全部是0，那根据我们转换的规则，由于符号位为1，所以，负零所对应的反码就应该是1，后边全部变成1

• 除了反码的整数之外，反码的小数和原码也是一一对应的，所以反码的小数的一个表示范围与原码也是相同的，同样负零和正零会有两种形式

• 即：

  • $[+0{]}_{原}=00000000$
  • $[-0{]}_{原}=10000000$
  • $[+0{]}_{反}=00000000$
  • $[-0{]}_{反}=11111111$

• 实际上，反码只是原码转变成补码的过程当中的一个中间状态，反码在具体应用中的意义并不是很大

• 计算机硬件不会使用反码直接进行加减乘除这些运算

补码

• 我们基于反码来得到补码, 对于一个正数来说，正数的补码它所对应的补码其实就是原码

• 而对于一个负数来说，负数所对应的补码我们可以用反码的末位加一这样的方式迅速的进行转换

• 那加一的过程中我们需要考虑到进位的问题, 首先来看用补码来表示定点的整数

• 对于正19这个数来说，由于它是一个正数，所以这个真值它所对应的补码形式其实和原码是一模一样的

  • x = +19D
    • $[x{]}_{原}=0,0010011$
    • $[x{]}_{反}=0,0010011$
    • $[x{]}_{补}=0,0010011$

• 再来看负19，由于这个真值是一个负数，或者说这个符号为它为1，因此我们在求这个真值所对应的补码的时候

• 就需要先把原码的这些尾数全部取反得到反码，然后再在反码的末尾这一位再加上一个一

• 因此，负19所对应的补码就应该是这个样子，比起反码来说，末位加了一个一

  • x = -19D
    • $[x{]}_{原}=1,0010011$
    • $[x{]}_{反}=1,1101100$
    • $[x{]}_{补}=1,1101101$

• 再来看用补码表示的小数，正的0.75这个小数它的原码如下，那由于这是一个正数，所以它所对应的补码形式和原码是一模一样的

• 我们只需要把原码照搬下来就可以

  • x = +0.75D
    • $[x{]}_{原}=0.1100000$
    • $[x{]}_{反}=0.1100000$
    • $[x{]}_{补}=0.1100000$

• 然后再来看负的0.75，由于它是一个负数，所以我们首先需要把原码的尾数部分全部取反

• 然后再在反码的末位加上一个1，需要注意进位的问题，末位的这两个1相加等于0，往高位进1, 1加1又等于零

• 再往高位进1，那直到进到小数点后第2位的位置，0加1等于1，再往前就不会再有进位了

• 好，所以这就是负的0.75这个真值它所对应的补码形式

  • x = -0.75D
    • $[x{]}_{原}=1.1100000$
    • $[x{]}_{反}=1.0011111$
    • $[x{]}_{补}=1.0100000$

补码的正零和负零问题

• 首先看正零，由于符号位为0，所以按照刚才提出的规则，符号位为零，那么它所对应的补码正零所对应的补码和原码是一样的，都是零
• 再来看负零，由于符号位为1，所以我们把它看为一个负数，因此负零它所对应的补码形式应该是先把它转换成反码，然后再在反码的末位加一，也就是八个1的末位再加一个1
• 那这个加法的结果应该是8个0，然后更高位第9个位会进一个1，但是由于这个地方我们规定机器字长只有8个位，所以我们向更高位进的这个1其实会被丢弃
• 而低八位留下的这八个零是和我们刚才推出的正零这种状态发生了重合, 因此我们用补码的形式来表示真值零，它只会有一种表示形式，就是全零这种方式

• $[+0{]}_{原}=00000000$
• $[-0{]}_{原}=10000000$
• $[+0{]}_{反}=00000000$
• $[-0{]}_{反}=11111111$

• 问题来了，原码当中有两个二进制的状态会对应零这个真值，而在补码中只有其中一种状态表示零，那多出来的这种二进制状态怎么办呢？
• 对于这个问题我们有一个特别的规定，对于定点整数的补码来说，如果符号位为1，后续这些都是零的话，那么我们规定这个补码它所对应的数值是负的二的七次方
  • 即：$[x{]}_{补}=1,0000000$ 表示 $x=-2^7$
• 对于八位的原码和反码来说，八位所能表示的最小数值应该是负的二的七次方减一，即：$-(2^7-1)$
• 而对于补码来说，它可以多表示一个负数，最小可以表示到负的二的七次方，即：$-2^7$
• 因此，如果机器字长是n+1位，那么补码整数的表示范围应该是这样的，$-2^n\le x\le 2^n-1$, 会比原码和反码多一个$-2^n$
• 而如果用补码表示定点小数也有类似的问题，由于正零和负零只有一种表示形式，因此多出来的这个二进制状态，也就是符号位为1，后续全为0
• 这种状态我们会规定它所对应的值是-1，原码和反码所能表示的最小值应该是 $-(1-2^{-n})$，而补码可以多表示一个-1
• 因此同样是n+1个比特位，补码会比原码、反码的表示范围更多一个数，不管是整数还是小数都这样
• 如果我们知道了一个正数的补码，那么想要知道它所对应的原码是很容易的，因为正数的原码和补码是相同的
• 但是如果给你一个负数的补码，符号位为一，那么想要推出它所对应的原码应该怎么办呢？
• 其实这个逆向转换的过程和正向转换的过程是一样的，同样是让尾数全部取反，然后末位加一
• 好来看一下，比如说通过-19的补码来求它的原码
  • 我们基于上面的例子，-19的补码是：$[-19{]}_{补}=1,1101101$
  • 那么我们首先要把这些尾数全部取反，0变1, 1变0，然后在末尾加1, 那得到的结果就是10010010，最后零加一等于一, 即：10010011
  • 因此对于一个负数来说，原码转变成补码，还有补码逆向的转变为原码，方法都是一样的，都是尾数全部取反，然后末尾加一
• 再来看一个小数的例子， 通过-0.75的补码求它的原码
  • -0.75的补码是：$[-0.75{]}_{补}=1.0100000$
  • 那么首先需要把它的尾数全部取反，1011111，然后再在末尾加一，那加了一之后会有一系列的进位，最后得到的结果应该是1.11，然后后边都是零
  • 所以用这种方式可以得到它所对应的原码，这种算法是没有问题的

移码

• 移码很简单，就是在补码的基础上把补码的符号被取反就可以, 需要注意，移码只能用于表示整数，而不能用于表示小数

• 正19的补码已经得到了，只需要把它的符号位取反，就可以得到与之对应的移码

• 负19也是类似的，只需要把补码的符号位取反，就可以得到与之对应的移码

  • x = +19D
    • $[x{]}_{原}=0,0010011$
    • $[x{]}_{反}=0,0010011$
    • $[x{]}_{补}=0,0010011$
    • $[x{]}_{移}=1,0010011$
  • x = -19D
    • $[x{]}_{原}=1,0010011$
    • $[x{]}_{反}=1,1101100$
    • $[x{]}_{补}=1,1101101$
    • $[x{]}_{移}=0,1101101$

• 那由于移码是由补码转换过来的，所以移马和补马的这些数的表示肯定也是一一对应的

• 也就是说，移码的正零和负零它同样只有一种表示形式

• 另外，移码整数的表示范围和补码也会保持一致，这是因为移码和补码是一一映射，一一对应的关系。

移码作用

• 所有的补码的符号位取反就得到了移码，那你会发现，如果把移码的所有二进制位看作是一个无符号数，那么当真值增大的时候，上图从上向下观察
• 移码所对应的这个无符号数，它也是在逐一递增的，所以移码的这种特性就保证了我们可以用计算机硬件来很方便的实现两个移码之间的大小对比
• 如果要对比两个移码的大小，那么我们可以让计算机硬件从第一个，也就最高位的这个比特一次往后对比
• 谁先出现1，那么就谁更大，而如果说两个都同时出现1，继续往后对比就可以
• 总之，移码的这种特性可以让计算机硬件很方便的判断出哪一个真值更大

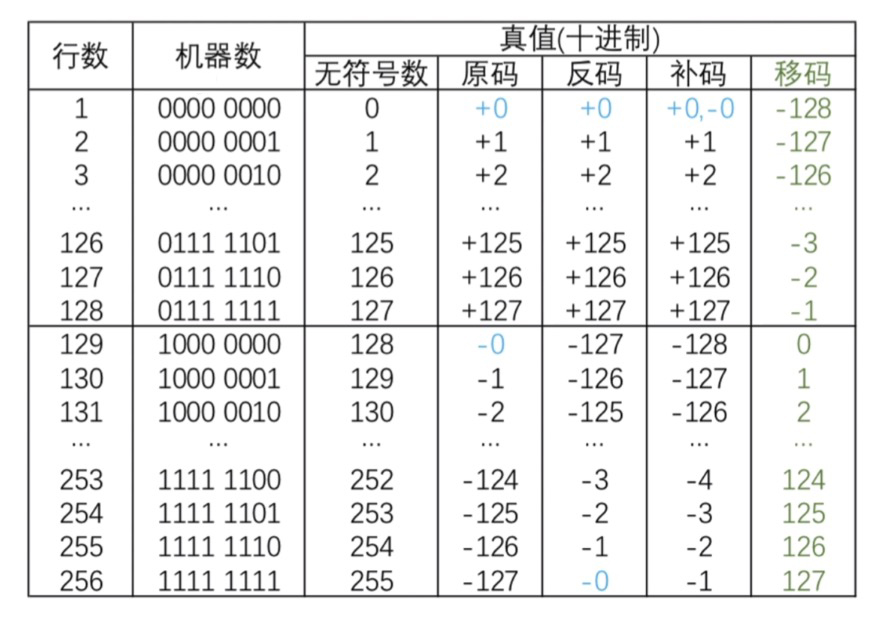
• 以上是定点整数关于源码，反码，补码，移码的示例，因为移码只能表示整数不能表示小数
• 原码和反码都有正零和负零这样的两种真值零的状态，而补马和移码只有一种真值零的状态，所以补马和移玛可以表示更多一个的负数

更多示例

1 ) 定点整数x等于正的50，用8位的原码、砝码、补码和移码来表示

• x = +50D
  • $[x{]}_{原}=0,0110010$
  • $[x{]}_{反}=0,0110010$
  • $[x{]}_{补}=0,0110010$
  • $[x{]}_{移}=1,0110010$

2 ) 定点整数x等于负的100，用8位的原码、砝码、补码和移码来表示

• x = -100D
  • $[x{]}_{原}=1,1100100$
  • $[x{]}_{反}=1,0011011$
  • $[x{]}_{补}=1,0011100$
  • $[x{]}_{移}=0,0011100$

3 ) 求下列各种码(值为负)对应的真值

• $[x{]}_{原}=10001101$
  • x = -13D
• $[x{]}_{反}=10001101$
  • 首先恢复成原码：1110010
  • x = -114D
• $[x{]}_{补}=10001101$
  • 首先恢复成原码，两者(原码，补码)互转的规则一致：把尾数每位取反，再末位加1, 即：11110011
  • x = -115D
• $[x{]}_{移}=10001101$
  • 首先恢复成补码，即：00001101，这是一个正数，直接得到原码，00001101
  • x = +13D

4 ) 求下列各种码(值为正)对应的真值

• $[x{]}_{原}=00001101$
  • x = 13D
• $[x{]}_{反}=00001101$
  • x = 13D
• $[x{]}_{补}=00001101$
  • x = 13D
• $[x{]}_{移}=00001101$
  • 首先把移码的符号位由0变为1，得到与之对应的补码，即：10001101
  • 再由这个补码得到原码
  • x = -115D

5 ) 由$[x{]}_{补}$ 快速求 $[-x{]}_{补}$的方法

• 常规做法是由补码恢复成原码，再通过原码求 $[-x{]}_{补}$
• 快速做法：符号位、数值位全部取反，末位 + 1
• 由上述示例中我们可知
  • -115的补码是： 10001101
  • 经过： 符号位、数值位全部取反，末位 + 1
  • 得到：01110010，这个就是115的补码

总结

• 移码只能用于表示整数，而不能用于表示定点小数
• 无论是用哪种码，只要我们表示的是定点整数，我们都默认小数点是隐含在最低位的后面
• 对于定点小数来说，无论我们用哪种码，我们都默认小数点是隐含在符号位的后面
• 各种码对真值零的表现形式
  • 原码和反码有+0和-0这样的两种状态
  • 而补码和移码表示真值0只能有一种表示形态
  • 整数的表示范围
    • 原码和反码：$-(2^n-1)\le x\le 2^n-1$
    • 补码和移码：$-2^n\le x\le 2^n-1$
  • 小数的表示范围
    • 原码和反码：$-(1-2^n)\le x\le 1-2^n$
    • 补码：$-1\le x\le 1-2^{-n}$
    • 移码：移码全0真值最小，移码全1真值最大, 基于此特性，两个移码之间可以通过计算机硬件来比较大小